Sbírka řešených úloh

Magnetické pole vodičů s proudem

Úloha číslo: 51

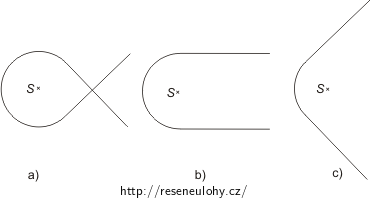
Na obrázku jsou tři části různých elektrických obvodů, z nichž se každý skládá z vodiče zakřiveného do tvaru kruhového oblouku (všechny mají stejný poloměr) a dvou dlouhých přímých úseků, které mají směr tečny k oblouku. Vodiče se kříží bez dotyku. Ve všech třech případech protéká vodiči stejný proud. Seřaďte úseky sestupně podle velikosti výsledné magnetické indukce ve středu oblouku.

• Nápověda

  Uvědomte si, jaké vztahy platí pro magnetické pole přímého vodiče a kruhového oblouku. Jak určíme směr magnetické indukce?

• Rozbor

  Abychom úlohu vyřešili co nejjednodušším způsobem, rozdělíme vodič pomyslně na tři části — kruhový oblouk a dvě polopřímky. Poté použijeme rovnice pro velikost magnetické indukce pro každou z těchto částí. Příspěvky od každé části vodiče v bodě S sečteme a porovnáme s hodnotami dalších vodičů.

• Řešení

  Nejdříve určíme magnetické pole vytvořené vodičem ve tvaru kruhového oblouku. Pro velikost magnetické indukce ve středu oblouku platí vztah

  \[B_0=\frac{\mu_0 I \varphi}{4 \pi R},\]

  kde za úhel φ dosadíme úhel v obloukové míře („v radiánech“).

  Při výpočtu příspěvků magnetické indukce od přímých úseků si nejprve připomeneme vztah pro magnetickou indukci nekonečně dlouhého vodiče

  \[B = \frac{\mu_0 I}{2\pi l}.\]

  V našem případě máme pouze „polovinu nekonečně dlouhého vodiče“. Díky symetrii přispívají obě poloviny stejně, a proto bude velikost magnetické indukce od přímého úseku B₁ poloviční

  \[B_\mathrm{p} = \frac{\mu_0 I}{4\pi l}.\]

  Pro určení směru magnetické indukce použijeme pravidlo pravé ruky, které říká: Položte palec pravé ruky ve směru proudu, zahnuté prsty ukazují směr indukčních čar v okolí dané části vodiče. Nakreslíme si, jak bude vypadat magnetická indukce od jednotlivých úseků vodičů.

  

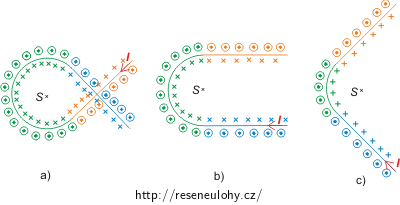
  Z obrázků vidíme, že magnetické indukce od jednotlivých částí vodiče se uvnitř smyčky sčítají.

  Celková magnetická indukce tedy bude součet magnetické indukce od obloukového vodiče a od přímých vodičů:

  \[B= B_0 + 2B_\mathrm{p}.\]

  Příspěvky od přímých vodičů budou pro všechny tři příklady stejné. Velikost celkové magnetické indukce závisí pouze na velikosti magnetické indukce od obloukového vodiče.

   

  a) Oblouk tvoří tři čtvrtiny kruhu, za úhel φ proto dosadíme

  \[\varphi = \frac{3}{2}\pi.\]

  Magnetická indukce vytvořená kruhovým obloukem je potom

  \[B_0=\frac{3\mu_0 I}{8 R}.\]

  Celková indukce od vodiče a v bodě S má velikost:

  \[B_a=\frac{\mu_0 I}{2\pi l} + \frac{3\mu_0 I }{8 R}.\]

   

  b) Oblouk tvoří polovina kruhu, za úhel dosadíme

  \[\varphi = \pi.\]

  Magnetická indukce vytvořená od kruhového oblouku je

  \[B_0=\frac{\mu_0 I }{4R}.\]

  Celková indukce od vodiče b v bodě S má velikost:

  \[B_b=\frac{\mu_0 I}{2\pi l} + \frac{\mu_0 I }{4 R}.\]

   

  c) Oblouk tvoří čtvrtina kruhu, za úhel dosadíme

  \[\varphi = \frac{\pi}{2}.\]

  Magnetická indukce vytvořená od kruhového oblouku je

  \[B_0=\frac{\mu_0 I }{8R}.\]

  Celková indukce od vodiče c v bodě S má velikost:

  \[B_c=\frac{\mu_0 I}{2\pi l} + \frac{\mu_0 I }{8 R}.\]

   

  Shrnutí

  Velikosti magnetických indukcí od jednotlivých vodičů:

  \[B_a=\frac{\mu_0 I}{2\pi l} + \frac{3\mu_0 I }{8 R}\] \[B_b=\frac{\mu_0 I}{2\pi l} + \frac{\mu_0 I }{4 R}\] \[B_c=\frac{\mu_0 I}{2\pi l} + \frac{\mu_0 I }{8 R}.\]

  Velikosti jednotlivých indukcí se liší pouze ve velikosti příspěvku magnetické indukce od oblouku. Tento příspěvek je úměrný délce oblouku, proto je největší ve vodiči s nejdelším obloukem.

  Vodiče seřadíme sestupně podle velikosti magnetických indukcí v bodě S:

  \[B_a > B_b > B_c.\]

• Odpověď

  Největší magnetickou indukci v bodě S „vytvoří“ vodič a, pak následuje vodič b a nejmenší magnetická indukce v bodě S bude u vodiče c.