Sbírka řešených úloh

Vyvážený můstek

Úloha číslo: 292

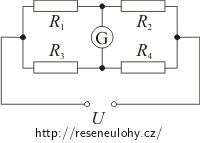
Můstek s rezistory R₁, R₂, R₃ a s rezistorem, jehož odpor R₄ závisí na teplotě, je vyvážen. Určete teplotu t rezistoru R₄.

Při teplotě 0 °C (tzv. vztažná teplota) má odpor rezistoru R₄ hodnotu 4,5 kΩ, teplotní součinitel odporu se rovná 0,004 °C^-1 a hodnoty ostatních rezistorů jsou R₁ = 2,0 kΩ; R₂ = 2,3 kΩ; R₃ = 4,0 kΩ.

• Nápověda 1

  Uvědomte si nebo vyhledejte, co znamená, že je můstek vyvážen?

• Řešení nápovědy 1

  Jestliže je můstek vyvážen, znamená to, že galvanometrem G neprotéká žádný proud.

• Nápověda 2

  Uvědomte si, jak vypočítáme odpor teplotně závislého rezistoru.

• Řešení nápovědy 2

  Odpor teplotně závislého rezistoru R vypočítáme ze vztahu:

  \[R\,=\,R_0\left(1+\alpha \Delta t\right),\]

  kde R je odpor rezistoru při teplotě t, R₀ odpor rezistoru při počáteční (tzv. vztažné) teplotě t₀, α je teplotní součinitel elektrického odporu a Δt je rozdíl teplot Δt = t₀.

• Nápověda 3

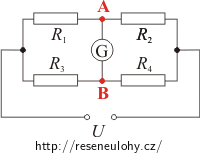
  Uvědomte si, jaké je napětí mezi body A a B, pokud galvanometrem neprotéká proud. Co to znamená pro elektrický potenciál těchto bodů?

  

• Řešení nápovědy 3

  Jestliže mezi body A a B neprotéká proud, pak mezi nimi musí být nulové napětí. Pokud by napětí nulové nebylo, potom by mezi těmito body tekl proud.

  Protože napětí mezi dvěma body se rovná rozdílu jejich elektrického potenciálu, musí mít body A a B stejný elektrický potenciál. Odtud plyne, že hodnoty napětí na rezistorech R₁ a R₃ jsou si rovny (stejně tak i hodnoty napětí na rezistorech R₂ a R₄).

• Rozbor

  

  Jestliže je můstek vyvážen, znamená to, že galvanometrem G neprotéká žádný proud. Platí tedy:

  1. Proud protékající rezistorem R₁ se bude rovnat proudu, který protéká rezistorem R₂ (to samé platí i pro rezistory R₃ a R₄).
  2. Napětí mezi body A a B je nulové. Napětí mezi dvěma body je rovno rozdílu jejich potenciálu, uzly A a B mají tedy stejný elektrický potenciál. Z toho plyne, že hodnoty napětí na rezistorech R₁ a R₃ jsou si rovny (obdobně i pro rezistory R₂ a R₄).

  Z těchto dvou úvah a použitím Ohmova zákona pro část obvodu (úbytek napětí na spotřebiči se rovná součinu odporu spotřebiče a proudu, který spotřebičem protéká) získáme pravidlo, které platí pro vyvážený můstek: podíl odporů rezistorů R₁ a R₂ je stejný jako podíl odporů rezistorů R₃ a R₄.

  Odpor rezistoru R₄ je závislý na teplotě. Odpor teplotně závislého rezistoru vypočítáme pomocí vztahu:

  \[R_4\,=\,R_0\left(1\,+\,\alpha \Delta t\right),\]

  kde R₄ je odpor rezistoru při teplotě t, R₀ odpor rezistoru při počáteční (tzv. vztažné) teplotě t₀, α je teplotní součinitel elektrického odporu a Δt je rozdíl teplot Δt = t − t₀.

• Řešení

  

  Pokud je můstek vyvážen, znamená to, že galvanometrem G neprotéká žádný proud. Uzly A a B proto budou mít stejný elektrický potenciál a platí:

  1. Proud protékající rezistorem R₁ se rovná proudu, který protéká rezistorem R₂. A proud protékající rezistorem R₃ se rovná proudu protékajícímu rezistorem R₄. Tedy:

  \[I_1\,=\,I_2\] \[I_3\,=\,I_4.\]

  2. Protože uzly A a B mají stejný elektrický potenciál, jsou hodnoty napětí na rezistorech R₁ a R₃ stejné. To samé platí i pro rezistory R₂ a R₄:

  \[U_1\,=\,U_3\] \[U_2\,=\,U_4.\]

  Ohmův zákon pro část obvodu říká, že

  \[U_\mathrm{x}\,=\,R_\mathrm{x}I_\mathrm{x},\]

  kde U_x je úbytek napětí na spotřebiči, R_x odpor spotřebiče a I_x je proud, který spotřebičem protéká.

  Nyní si pomocí tohoto vztahu vyjádříme rovnosti napětí na rezistorech:

  \[R_1I_1\,=\,R_3I_3\] \[R_2I_2\,=\,R_4I_4.\]

  Obě rovnice podělíme:

  \[\frac{R_1I_1}{R_2I_1}\,=\,\frac{R_3I_3}{R_4I_3}.\]

  Proudy I₁ a I₃ se ve zlomcích zkrátí a my tak získáme podmínku pro vyvážený můstek:

  \[\frac{R_1}{R_2}\,=\,\frac{R_3}{R_4}.\]

  Nyní si z ní vyjádříme odpor R₄:

  \[R_4\,=\,\frac{R_2R_3}{R_1}.\tag{*}\]

  Odpor rezistoru R₄ je závislý na teplotě. Tuto závislost udává vztah

  \[R_4\,=\,R_0\left(1\,+\,\alpha \Delta t\right),\]

  kde R₄ je odpor rezistoru při teplotě t, R₀ odpor rezistoru při vztažné teplotě t₀, α je teplotní součinitel elektrického odporu a Δt je rozdíl teplot Δt = t − t₀.

  Z této rovnice si vyjádříme teplotní rozdíl Δt:

  \[1\,+\,\alpha\Delta t\,=\,\frac{R_4}{R_0}\] \[\alpha\Delta t\,=\,\frac{R_4}{R_0}-1\,=\,\frac{R_4-R_0}{R_0}\] \[\Delta t\,=\,t-t_0\,=\,\frac{\frac{R_4-R_0}{R_0}}{\alpha}\,=\,\frac{R_4-R_0}{\alpha R_0}.\]

  Pro teplotu t tedy platí:

  \[t\,=\,\frac{R_4-R_0}{\alpha R_0}\,+\,t_0.\]

  Nyní do tohoto vzorce dosadíme za R₄ vztah (*):

  \[t\,=\,\frac{\frac{R_2R_3}{R_1}-R_0}{\alpha R_0}\,+\,t_0,\]

  tím získáme výsledný vztah pro výpočet teploty t rezistoru R₄:

  \[t\,=\,\frac{R_2R_3\,-\,R_0R_1}{\alpha R_0R_1}\,+\,t_0.\]

• Zápis a číselné dosazení

  Ze zadání úlohy víme:

  R1 = 2,0 kΩ	odpory rezistorů R1, R2, R3 můstku
  R2 = 2,3 kΩ
  R3 = 4,0 kΩ
  R0 = 4,5 k Ω	odpor rezistoru R4 při teplotě 0 °C
  α = 0,004 °C-1	teplotní součinitel elektrického odporu rezistoru R4
  t = ? (°C)	teplota rezistoru R4

  ---

  Poznámka: Protože všechny odpory jsou vyjádřeny v kiloohmech a ve vzorci se nám jednotka ohm zkrátí, nemusíme odpory rezistorů převádět na základní jednotky:

  \[ t\,=\,\frac{R_2R_3\,-\,R_0R_1}{\alpha R_0R_1}\,+\,t_0\,=\,\frac{2{,}3{\cdot} 4-4{,}5{\cdot} 2}{0{,}004{\cdot} 4{,}5{\cdot} 2}\,{}^\circ\mathrm{C}\,+\,0\,{}^\circ\mathrm{C}\,=\,5{,}5\,{}^\circ\mathrm{C}.\]

• Odpověď

  Jestliže je můstek vyvážen, pak teplota rezistoru R₄ je 5,5 °C.

• Jiný způsob řešení úlohy

  Dalším možným, avšak dosti komplikovaným způsobem řešení této úlohy, je použití Kirchhoffových zákonů. Vyjádříme si proud procházející galvanometrem za obecných podmínek a potom hledáme, kdy bude nulový.

  Znění Kirchhoffových zákonů a „kuchařku“ k jejich použití naleznete v úloze Použití Kirchhoffových zákonů pro řešení obvodu se dvěma zdroji.

• Komentář

  Měřicí můstky se používají k měření elektrických veličin – kapacity, odporu nebo indukčnosti. Měření můstkovými metodami se zakládá na dosažení rovnováhy mezi větvemi můstků. Tuto rovnováhu zjišťujeme galvanometrem, který je připojen k jedné úhlopříčce můstku. Ke druhé úhlopříčce je připojen zdroj napětí – stejnosměrný nebo střídavý, podle měřené veličiny (střídavé napájení pro kapacitu a indukčnost, pro odpory stejnosměrné i střídavé, lepší je však stejnosměrné).

  Měření pomocí můstkové metody je velmi přesné, ale vyhovuje jen úzkému rozsahu hodnot (záleží na parametrech můstku).

  Na principu můstkové metody jsou založeny přístroje speciálně konstruované pro přímé měření elektrických odporů v technické praxi. Nazývají se ohmmetry.

• Dynamický prvek

  Následující aplet zobrazuje rezistorový můstek. Pomocí posuvníku se nastavuje velikost odporu na rezistoru čtyři. Uprostřed se vypisuje hodnota proudu protékající galvanometrem a také je zde šipka, která zobrazuje směr proudu.

   

  Úlohy pro práci s aplety

  1. Nastavujte různé hodnoty \(R_4\) a pozorujte, že napětí na \(R_1\) a \(R_3\) (resp. \(R_2\) a \(R_4\)) jsou stejná, galvanometr funguje jako „uzel.“
  2. Nalezněte takovou hodnotu \(R_4\), aby galvanometrem neprotékal proud. Porovnejte proudy a napětí na jednotlivých rezistorech, zaměřte se také na jejich vzájemné poměry. Svá pozorování srovnejte s řešením úlohy.