Okamžité napětí generátoru
Úloha číslo: 165
Generátor s okamžitým napětím u(t) = 25sin(377t) je připojen k cívce o indukčnosti 12,7 H.
Pozn.: Do rovnice pro okamžité napětí nebudeme pro přehlednost psát jednotky. Budeme brát jednotky nenásobné, tedy například čas dosazujeme v sekundách atd.
Zápis
Ze zadání známe:
Okamžité napětí generátoru: u(t) = 25sin(377t) Indukčnost cívky: L = 12,7 H Chceme určit:
a) Amplitudu proudu: Im = ? (A) b) Napětí, je-li proud maximální: Ub = ? (V) c) Proud, je-li napětí Uc = 12,5 V: Ic = ? (A) Nápověda 1
Rozmyslete si, co znamenají ve vzorci pro okamžité napětí jednotlivé číselné hodnoty.
Nápověda 2
Pro výpočet maximální hodnoty proudu, nebo-li amplitudy proudu, použijeme Ohmův zákon pro střídavý proud.
Nápověda 3
Jak je fázově posunuto napětí s proudem, máme-li v obvodu zařazenou cívku?
Rozbor
Úloha je rozdělena na tři části, které budeme řešit postupně:
a) Známe-li průběh okamžitého napětí v obvodu, známe i amplitudu napětí. Amplitudu proudu (= maximální proud) získáme z Ohmova zákona. Impedanci v Ohmově zákoně zde tvoří pouze induktance cívky, kterou lze vypočítat z indukčnosti cívky zařazené v obvodu.
b) Nejprve vyjádříme průběh okamžitého proudu v obvodu. V tomto obvodu je zařazena cívka, to znamená, že napětí předbíhá proud o π/2. Potom určíme čas, ve kterém proud dosahuje maximální hodnoty. Ten dosadíme do časového průběhu napětí.
c) Postup v tomto úkolu bude obdobný jako u úkolu b). Vyjádříme si čas t, ve kterém je napětí 12,5 V. Vzhledem k průběhu sinusové funkce dostaneme více časů pro toto napětí. Z těchto časů si vybereme ty, ve kterých napětí dále klesá, a dosadíme je do vyjádření okamžité hodnoty proudu.
Rozbor vzorce pro popis okamžitého napětí
Porovnáme vzorec pro obecné vyjádření okamžitého napětí se zadanou závislostí:
\[u(t)=U_\mathrm{m}\sin\left(\omega t+ {\varphi}_{0u}\right)=25\sin\left(377t\right).\]Odtud vidíme, že:
\[U_\mathrm{m}=25\,\mathrm V\] \[\omega=377\,\mathrm s^{-1}.\]a) Řešení
Použijeme Ohmův zákon
\[I_\mathrm{m}=\frac{U_\mathrm{m}}{Z}\]a za impedanci dosadíme induktanci cívky:
\[I_\mathrm{m}=\frac{U_\mathrm{m}}{Z}=\frac{U_\mathrm{m}}{X_L}=\frac{U_\mathrm{m}}{\omega L}.\]
Číselně dosadíme a vyjde nám:
\[I_\mathrm{m}=\frac{25}{377 {\cdot} 12{,}7}\,\mathrm A\,\dot{=}\,5{,}2 \,\mathrm mA.\]b) Řešení
Napíšeme si rovnici pro vyjádření okamžité hodnoty proudu. Amplitudu proudu jsme si vypočítali v oddíle a) a fázový posun mezi proudem a napětím je -π/2, protože v obvodu je zařazena jen cívka. Napětí předbíhá proud, nebo-li proud se opožďuje za napětím:
\[i\left(t\right)=I_m \sin\left(\omega t + {\varphi}_{0i}\right)=5{,}2 {\cdot} 10^{-3}\sin\left(377t- \frac{\pi}{2}\right).\]Chceme najít okamžik, kdy je proud maximální, to znamená, že i(t) = Im:
\[i\left(t\right)=I_\mathrm{m}\,\sin\left(377t-\frac{\pi}{2}\right),\] \[I_\mathrm{m}=I_\mathrm{m}\,\sin\left(377t-\frac{\pi}{2}\right),\] \[1=\sin\left(377t-\frac{\pi}{2}\right),\] \[\frac{\pi}{2}=377t-\frac{\pi}{2},\] \[t=\frac{\pi}{377}\,\mathrm s.\]Velikost napětí při maximálním proudu získáme dosazením do vzorce, který vyjadřuje okamžitou hodnotu napětí:
\[U_\mathrm{b}=25\,\sin\left(377t\right)=25\,\sin\left(377 \cdot \frac{\pi}{377}\right)\,\mathrm V=25\,\sin\left(\pi\right)\,\mathrm V=0\,\mathrm V.\]
Nulovou hodnotu napětí při maximálním proudu jsme mohli předpovídat i bez výpočtu, protože oba průběhy okamžitých hodnot jak proudu, tak napětí popisuje sinusová funkce. V případě cívky jsou tyto „sinusovky” posunuté přesně o π/2. Takže pokud jedna ze „sinusovek” nabývá maxima, musí být druhá v minimu. Prohlédněte si obrázek v následující sekci řešení.
c) Řešení
Chceme určit velikost proudu při napětí Uc = 12,5 V.
\[U_\mathrm{c}=25\sin\left(377t\right),\] \[12{,}5=25\,\sin\left(377t\right),\] \[\sin\left(377t\right)=\frac{1}{2}.\]Úlohu budeme řešit pouze v první periodě sinusové funkce popisující průběh okamžitého napětí. V dalších periodách bychom získali stejné výsledky. Získáme dva časy, ve kterých napětí nabývá požadovanou hodnotu:
\[377t= \frac{\pi}{6 }\,\mathrm s, \tag{1}\] \[377t= \frac{5\pi}{6 }\,\mathrm s .\tag{2}\]Kterou hodnotu máme zvolit, zjistíme z obrázku, do kterého zakreslíme časový průběh napětí a proudu.
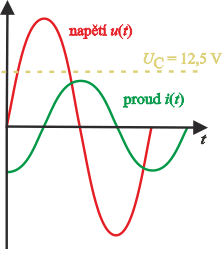
Na obrázku je žlutou čerchovanou čárou znázorněno napětí 12,5 V.
Hodnota, kterou hledáme, je: \(377t= \frac{5\pi}{6 }\,\mathrm s \), protože napětí má dále klesat.
Dosadíme do vzorce pro výpočet okamžité hodnoty proudu a získáme hodnotu proudu při napětí 12,5 V:
\[I_\mathrm{c}=5{,}2 {\cdot} 10^{-3}\sin\left(377t- \frac{\pi}{2}\right)=5{,}2 {\cdot} 10^{-3}\sin\left( \frac{5\pi}{6 } - \frac{\pi}{2}\right)\,\mathrm A=5{,}2 {\cdot} 10^{-3}\sin\left(\frac{\pi}{3}\right)\,\mathrm A\,\dot{=}\,4{,}5\,\mathrm mA. \]
Odpověď
Maximální hodnota proudu je přibližně: Im = 5,2 mA.
Je-li proud maximální, je hodnota napětí rovna asi: Ub = 0 V.
Je-li hodnota napětí 12,5 V a napětí dále klesá, má proud velikost přibližně: Ic = 4,5 mA.




