Sbírka řešených úloh

Biotův-Savartův zákon

Úloha číslo: 45

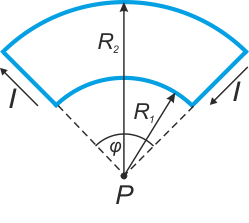
Použijte Biotův-Savartův zákon k výpočtu magnetické indukce B v bodě P, který je společným středem kruhových oblouků (čtvrtkruhů) o poloměrech 5 cm a 8 cm (viz obrázek). Oba oblouky jsou spojeny tak, že vytvářejí obvod, kterým protéká proud 10 A.

 

• Nápověda

  Uvědomte si, jak vypadá Biotův-Savartův zákon a jaký je výsledek jeho použití pro dlouhý přímý vodič a jaký pro kruhový oblouk.

• Nápověda - Biotův-Savartův zákon

  Biotův-Savartův zákon slouží k výpočtu magnetické indukce $\vec{B}$ v libovolně zvoleném bodě vytvořené proudem I. Jeho matematický zápis je

  $$\mathrm{d}\vec{B} = \frac{\mu_o}{4\pi}\, \frac{I\, \mathrm{d}\vec{s}\times \vec{r}}{r^{3}},$$

  kde vektor magnetické indukce $\mathrm{d}\vec{B}$ má směr daný vektorovým součinem $\mathrm{d}\vec{s}\times\vec{r}$ a $\vec{r}$ je polohový vektor směřující od proudového elementu $I\mathrm{d}\vec{s}$ k bodu, ve kterém chceme magnetickou indukci určovat.

  Magnetickou indukci $\vec{B}$ získáme integrací Biotova-Savartova zákona podél proudové smyčky.

  Vektorový součin

  Velikost vektorového součinu $\left|\mathrm{d}\vec{s}\times\vec{r}\right|$ vypočítáme jako $\mathrm{d}s\, r\sin\alpha$, kde úhel α je úhel mezi vektory $\mathrm{d}\vec{s}$ a $\vec{r}$.

• Rozbor

  Abychom vyřešili úlohu co nejjednodušším způsobem, rozdělíme vodič pomyslně na čtyři části — dva oblouky a dva přímé vodiče. Poté vyjádříme magnetickou indukci pro každou z těchto částí.

  Úhel mezi rovným úsekem a spojnicí ke středu je buď přímý, nebo nulový. Z Biotova-Savartova zákona vyplývá, že příspěvky k magnetické indukci od těchto přímých vodičů jsou nulové, a tedy i magnetická indukce bude nulová. To znamená, že elektrický proud protékající rovnými úseky nevytváří žádné magnetické pole v bodě P.

  Pro kruhové oblouky použijeme také Biotův-Savartův zákon. Úhel mezi vektory $\mathrm{d}\vec{s}$ a $\vec{r}$ je pravý. Vzdálenost vodiče a místa, ve kterém magnetickou indukci určujeme, je pro daný oblouk konstantní a je rovna poloměru příslušného oblouku.

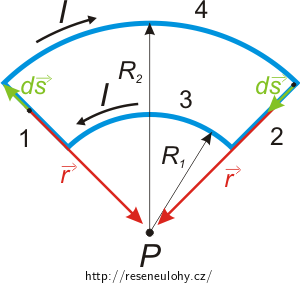
• Obrázek

  

• Řešení

  Smyčku pomyslně rozdělíme na čtyři úseky.

  Nejdříve budeme uvažovat rovný úsek 1. Pro výpočet magnetického pole použijeme Biotův-Savartův zákon

  $$\mathrm{d}B=\frac{\mu_0}{4\pi}\frac{I\mathrm{d}s\,\sin\alpha}{r^2},$$

  kde úhel α mezi $\mathrm{d}\vec{s}$ a $\vec{r}$ je roven α = 180°, a tedy sin α = 0. Elektrický proud protékající přímým úsekem 1 nevytváří žádné magnetické pole v bodě P.

  $$B_1= 0.$$

  Stejně je tomu i v případě přímého úseku 2, ve kterém je úhel α mezi $\mathrm{d}\vec{s}$ a $\vec{r}$ nulový pro každý proudový element. Tedy

  $$B_2 = 0.$$

  Zakřivené části 3 a 4 představují kruhový oblouk. Vztah pro výpočet magnetické indukce ve středu kruhového oblouku odvodíme také z Biotova-Savartova zákona. Úhel α, který svírají vektory $\mathrm{d}\vec{s}$ a $\vec{r}$, je 90° a r = R

  $$\mathrm{d}B=\frac{\mu_0}{4\pi}\,\frac{I\, \mathrm{d}s\, \sin 90^\circ}{R^{2}}= \frac{\mu_0}{4\pi}\,\frac{I \mathrm{d}s}{R^{2}}$$

  Velikost výsledné magnetické indukce v bodě P je rovna součtu (integrálu) všech příspěvků $\mathrm{d}\vec{B}$. Jelikož mají všechny příspěvky $\mathrm{d}\vec{B}$ stejný směr, stačí integrovat jejich velikost. Využijeme-li vztahu ds = R dφ (čímž změníme integrační proměnnou s na φ), dostaneme

  $$B = \int\,\mathrm{d}B = \int_0^\varphi {\frac{\mu_0}{4\pi}\,\frac {IR\mathrm{d}\varphi}{R^{2}} = \frac{\mu_0 I}{4\pi R} \int_0^\varphi 1\,\mathrm{d}\varphi}$$

  Po jednoduché integraci získáme vztah pro magnetickou indukci

  $$B=\frac{\mu_0 I}{4\pi R}\,\varphi$$

  Směr magnetických indukcí B₃ a B₄ určíme z vektorového součinu v Biotově-Savartově zákoně. Prsty pravé ruky orientujeme tak, že se „sklopí první vektor do druhého“. Vztyčený palec ukáže směr výsledného vektoru, tj. magnetické indukce. Odtud plyne známé Ampérovo pravidlo pravé ruky, ve kterém palec ukazuje směr proudu a zahnuté prsty směr magnetické indukce.

  

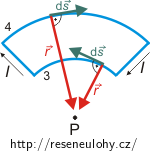
  Pomocí tohoto pravidla určíme směry magnetických indukcí B₃ a B₄ v bodě P. Magnetická indukce B₃ bude v bodě P kolmá k rovině obrázku a směřuje k nám. Magnetická indukce B₄ je v bodě P kolmá k rovině obrázku a směřuje od nás. Jelikož má magnetická indukce B₄ opačný směr než magnetická indukce B₃, v bodě P se budou odčítat.

  Výsledná magnetická indukce B vytvořená v bodě P proudem protékajícím smyčkou je dána vektorovým součtem jednotlivých příspěvků:

  $$\vec{B} = \vec{B_1}+\vec{B_2}+\vec{B_3}+\vec{B_4}$$ $$B=0+0+\frac{\mu_0I\varphi}{4\pi R_1}-\frac{\mu_0I \varphi}{4\pi R_2}$$ $$B= \frac{\mu_0I\varphi}{4\pi}\,\left( \frac{1}{R_1}-\frac{1}{R_2} \right)$$

  Jelikož je poloměr R₁ menší než poloměr R₂, je magnetická indukce B₃ od oblouku s poloměrem R₁ větší než magnetická indukce B₄ od oblouku s poloměrem R₂. Výsledná magnetická indukce v bodě P míří stejně jako magnetická indukce B₃, tedy před obrázek.

• Zápis a číselné dosazení

  $I= 10\,\mathrm{A}$	proud tekoucí obvodem
  $R_1=5\,\mathrm{cm}=0{,}05\,\mathrm{m}$	poloměr prvního oblouku
  $R_2=8\,\mathrm{cm}=0{,}08\,\mathrm{m}$	poloměr druhého oblouku
  $\varphi = \frac{\pi}{2}$	středový úhel příslušející oběma obloukům
  $B\,=\,?\,\mathrm{(T)}$	velikost magnetické indukce
  Z tabulek:
  $\mu_\mathrm{0} = 4 \pi\cdot 10^{-7}\,\mathrm{Hm^{-1}}$	permeabilita vakua

  ---

  $$B= \frac{\mu_\mathrm{0}I\varphi}{4\pi}\,\left(\frac{1}{R_1}-\frac{1}{R_2}\right)=\frac{4 \pi\cdot 10^{-7}\cdot10\cdot\frac{\pi}{2}}{4\pi}\,\left(\frac{1}{0{,}05}-\frac{1}{0{,}08}\right)\,\mathrm{T}\dot{=}\,12\,\mathrm{\mu T}$$

• Odpověď

  Magnetická indukce v bodě P míří za obrázek a má velikost

  $$B= \frac{\mu_oI\varphi}{4\pi}\,\left(\frac{1}{R_1}-\frac{1}{R_2}\right).$$

  Pro uvedené hodnoty vychází

  $$B\, \dot{=}\, 12\,\mathrm{\mu T}.$$