Alternátor střídavého proudu
Úloha číslo: 2314
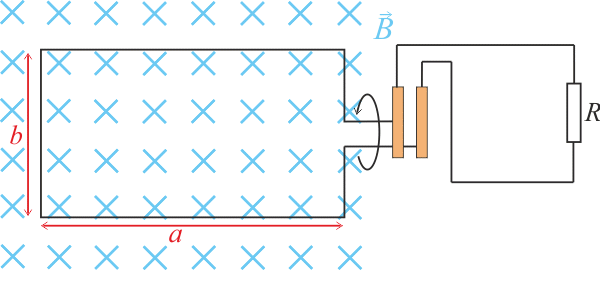
Obdélníková cívka délky a, šířky b s N závity rotuje s frekvencí f v homogenním magnetickém poli B, které míří do nárysny (viz obrázek). V čase \(t = 0\) je smyčka ve vertikální poloze (rovnoběžná s nárysnou) a při pohledu zleva v ose otáčení rotuje proti směru hodinových ručiček.
- Nakreslete obrázek alternátoru proudu při pohledu zleva vůči ose otáčení v čase \(\Delta t\) krátce po čase \(t =0\), když se smyčka otočila o úhel \(\alpha\) od vertikální osy. Na obrázku vyznačte vektor \(\vec{B}\), rovinu smyčky charakterizovanou normálovým vektorem \(\vec{n}\) a směr indukovaného proudu.
- Napište výraz pro magnetický indukční tok \(\Phi\) tekoucí smyčkou jako funkci času a zadaných parametrů.
- Odvoďte vztah pro indukované napětí.
- Navrhněte smyčku, která by vytvářela střídavé napětí o amplitudě \(U_\mathrm{i} = 120\space \mathrm{V}\) a frekvenci \(50\space \mathrm{Hz}\) v magnetickém poli \(0{,}4\space \mathrm{T}.\)
Nápověda
Jelikož máme rotující cívku v magnetickém poli, bude se na ní indukovat napětí, protože Faradayův zákon elektromagnetické indukce říká: Změní-li se magnetický indukční tok plochou vodivé smyčky za dobu \(\mathrm{d} t\) o \(\mathrm{d}\Phi\), vzniká ve vodiči indukované elektromotorické napětí, jež je dáno vztahem
\[U_\mathrm{i} = - \frac{\mathrm{d}\Phi}{\mathrm{d} t}.\]Magnetický indukční tok plochou o obsahu S je v případě homogenního pole definován jako \(\Phi=BS\cos\alpha\), kde \(\alpha\) je úhel, který svírá normála plochy s vektorem magnetické indukce \(\vec{B}.\) To, co se bude měnit v tomto případě, je právě úhel \(\alpha.\)
Jaká je časová závislost úhlu \(\alpha\), pokud se smyčka otáčí rovnoměrně?
K určení směru proudu indukovaném v cívce nám pomůže Lenzův zákon, který říká, že indukovaný proud má takový směr, aby svým magnetickým polem působil proti změně magnetického indukčního toku, která je jeho příčinou.
Řešení
a. Obrázek
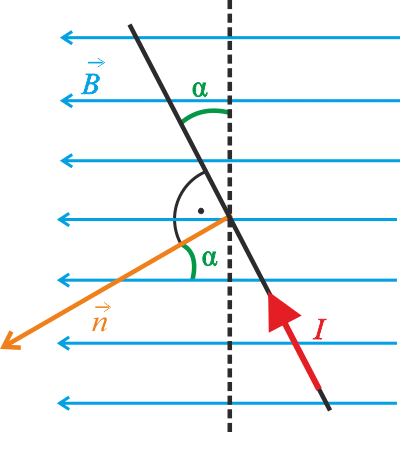
Nakreslíme obrázek situace při pohledu zleva. \(\alpha\) je úhel otočení a \(\vec{n}\) je normálový vektor k ploše smyčky. Lenzův zákon říká, že indukovaný proud má takový směr, aby svým magnetickým polem působil proti změně magnetického indukčního toku. Pokud se na situaci dívám zleva, tak se cívka otáčí protisměru hodinových ručiček a magnetický indukční tok cívkou se zmenšuje. Proud tedy musí téci v takovém směru, aby svým příspěvkem magnetický indukční tok zvětšoval (tj. jeho pole musí směřovat doleva). Z Ampérova pravidla pravé ruky pak dostáváme směr indukovaného proudu, viz obrázek.
b. Magnetický indukční tok
Jak bylo řečeno v nápovědě, magnetický indukční tok v homogenním poli \(B\) je definovaný následujícím vztahem
\[\Phi={B}{S}\cos\alpha,\]kde \(S\) je obsah smyčky a \(\alpha\) je úhel, který svírá normála plochy \(\vec{n}\) a vektor magnetické indukce \(\vec{B}\). Jelikož má smyčka N závitů, musíme tento obsah započítat N krát:
\[\Phi=BNab\cos\alpha.\]V předchozí části jsme označili úhel mezi normálou plochy \(\vec{n}\) a vektorem magnetické indukce \(\vec{B}\) jako \(\alpha\):
\[\Phi=BNab\cos\theta.\]Úhel \(\theta\) můžeme vyjádřit pomocí úhlové frekvence otáčení:
\[\theta = \omega t= 2\pi f t.\]Spojením posledních dvou vztahů dostaneme
\[\Phi=BNab\cos (2\pi f t).\tag{1}\]c. Indukované napětí
Vyjděme z Faradayova indukčního zákona, který nám říká
\[U_\mathrm{i} = - \frac{\mathrm{d}\Phi}{\mathrm{d} t}.\]Do výrazu dosaďme magnetický indukční tok (1), který jsme vyjádřili v předchozí části:
\[U_\mathrm{i} = - \frac{\mathrm{d}BNab\cos (2\pi f t)}{\mathrm{d} t}=2\pi f N Bab \sin(2\pi f t).\tag{2}\]d. Návrh smyčky
\(U_\mathrm{A}=120\ \mathrm{V}\) amplituda napětí \(f = 50\ \mathrm{Hz}\) frekvence \(B = 0{,}4\ \mathrm{T}\) magnetická indukce \(N = 1\) smyčka = 1 závit
Máme navrhnout smyčku, která bude indukovat střídavé napětí se zadanými parametry. Vraťme se k odvozenému vztahu pro okamžitou velikost indukovaného napětí (2):
\[U_\mathrm{i} =2\pi f N Bab \sin(2\pi f t).\]Jelikož se má jednat o smyčku, dosadíme \(N=1\). Pro amplitudu napětí \(U_\mathrm{A}\) platí
\[U_\mathrm{A} =2\pi f Bab.\]Nyní rovnici upravme tak, aby na levé straně zůstaly parametry, které neznáme, a na pravé straně byly zadané veličiny:
\[ ab= \frac{U_\mathrm{i}}{2\pi f B}.\]Po číselném dosazení získáme
\[ab\doteq 47{,}7\ \mathrm{m}^2.\]V případě čtvercové smyčky bude mít strana a velikost 6,9 m, což je opravdu hodně. Z tohoto důvodu se v alternátorech využívají cívky, které mají více závitů.
Dopočítejme, kolik by musela mít čtvercová cívka závitů, aby se na ní indukovalo stejné napětí, ale měla stranu délky \(a=10\space \mathrm{cm}\):
\[N=\frac{U_A}{2\pi f B a^2}\doteq 96.\]Odpověď
Pohled zleva na generátor nám ukazuje následující obrázek

Magnetický indukční tok tekoucí smyčkou v čase t je dán výrazem
\[\Phi=BNab\cos (2\pi f t).\]Indukované napětí na smyčce v čase t je dáno výrazem
\[U_\mathrm{i} =2\pi f N Bab \sin(2\pi f t).\]Pro obsah obecné obdélníkové smyčky o stranách a a b jsme odvodili vztah
\[ ab= \frac{U_\mathrm{i}}{2\pi f B}.\]Pokud by zadané parametry měla splnit čtvercová smyčka, musela by mít stranu dlouhou 6,9 m.

