Zahradní párty s rychlovarnou konvicí
Úloha číslo: 72
V domě je v zásuvce elektrické sítě napětí 230 V. Pomocí kabelu o délce 60 m a odporu 1,2 Ω je k této zásuvce na zahradě připojena varná konvice. Na konvici je tento štítek:
a) Jaké je skutečné napětí na topné spirále konvice a její skutečný příkon při uvedeném zapojení?
b) Sestrojte pro danou varnou konvici a daný průřez kabelu graf závislosti příkonu na délce kabelu od 0 do 2000 m.
Komentář
Protože v této úloze pracujeme s efektivními hodnotami napětí a proudu, můžeme úlohu řešit, jako by konvice byla zapojena do obvodu se zdrojem stejnosměrného napětí.
Efektivní hodnoty střídavého proudu a napětí odpovídají takovým hodnotám stejnosměrného proudu a napětí, při kterých je výkon stejnosměrného proudu v obvodu s odporem stejný jako výkon střídavého proudu.
Nápověda
Zamyslete se, co značí údaje na štítku konvice.
Rozbor
a) Skutečné napětí konvice a její skutečný příkon
Příkon elektrického proudu je roven součinu napětí na spotřebiči a proudu, který spotřebičem protéká. Tento proud se rovná podílu napětí na spotřebiči a odporu spotřebiče. Protože hodnoty napsané na štítku konvice určují její parametry, můžeme z napětí a příkonu, které jsou na tomto štítku uvedeny, vypočítat odpor konvice.
Kabel a varnou konvici můžeme pokládat za dva sériově spojené spotřebiče, proto oběma protéká stejný proud. Tento proud určíme z Ohmova zákona, do kterého dosadíme napětí zdroje (tj. napětí v zásuvce) a celkový odpor obvodu. Skutečné napětí na konvici bude úměrné protékajícímu proudu a odporu konvice.
Nyní již známe proud protékající konvicí i napětí na ní, a proto můžeme určit její skutečný příkon.
b) Závislost příkonu konvice na délce kabelu
Odpor kovového vodiče je přímo úměrný jeho délce a nepřímo úměrný jeho průřezu. Dále zavisí na měrném odporu vodiče (tj. na materiálu vodiče).
Při změně délky kabelu zůstává měrný odpor i průřez vodiče konstantní. Protože známe odpor kabelu při zadané délce, vyjádříme si pomocí těchto dvou veličin neznámý podíl měrného odporu a průřezu. Ten dosadíme do vyjádření odporu kabelu v závislosti na jeho délce.
Abychom zjistili závislost příkonu konvice na délce kabelu, nahradíme v rovnici pro příkon (kterou jsme získali řešením části a) odpor kabelu vztahem, který vyjadřuje odpor kabelu v závislosti na jeho délce.
Řešení části a): Skutečné napětí na topné spirále konvice
Kabel a varnou konvici můžeme pokládat za dva sériově spojené spotřebiče. Odpor kabelu označíme R0, odpor varné konvice (topné spirály) R.
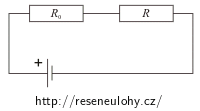
Z Ohmova zákona víme, že obvodem protéká proud I, pro který platí:
\[I\,=\,\frac{U_0}{R_0+R}\,,\]kde U0 je napětí na zdroji.
Protože kabel a konvici považujeme za sériově zapojené spotřebiče, pak celkový proud obvodem se rovná proudu protékajícímu spotřebičem:
\[I\,=\,\frac{U}{R}\,.\]Tyto dvě rovnice porovnáme:
\[\frac{U_0}{R_0+R}\,=\,\frac{U}{R}\,.\]A následně si vyjádříme skutečné napětí na spirále konvice U:
\[U\,=\,\frac{U_0R}{R_0+R}\,.\tag{*}\]Údaje 230 V a 2 000 W, které jsou na štítku konvice, říkají, že pokud konvici zapojíme ke zdroji o napětí Us = 230 V, bude její příkon Ps = 2 000 W. Z těchto hodnot vypočítáme odpor varné konvice R.
Pro příkon konvice platí:
\[P_\mathrm{s}\,=\,U_\mathrm{s}I\,=\,\frac{U_\mathrm{s}^2}{R}\,,\]kde Us je napětí na konvici a R je odpor konvice.
Z této rovnice určíme odpor R a za napětí a příkon dosadíme hodnoty ze štítku konvice. Tím zjistíme odpor topné spirály:
\[R\,=\,\frac{U_\mathrm{s}^2}{P_\mathrm{s}}\,.\]Takto vyjádřený odpor R dosadíme do rovnice (*):
\[U\,=\,\frac{U_0\frac{U_\mathrm{s}^2}{P_\mathrm{s}}}{R_0+\frac{U_\mathrm{s}^2}{P_\mathrm{s}}}\,=\,\frac{U_0U_\mathrm{s}^2}{P_s\left(R_0+\frac{U_\mathrm{s}^2}{P_\mathrm{s}}\right)}\]a získáme tak skutečné napětí na topné spirále konvice:
\[U\,=\,\frac{U_0U_\mathrm{s}^2}{P_\mathrm{s}R_0+U_\mathrm{s}^2}\,.\]Nyní již do této rovnice dosadíme číselné hodnoty veličin ze zadání úlohy: U0 = 230 V, R0 = 1,2 Ω, Ps = 2 000 W, Us = 230 V
\[U\,=\,\frac{230^3}{2\,000{\cdot}1{,}2+230^2}\,\mathrm{V}\,=\,220\,\mathrm{V}\,.\]Řešení části a): skutečný příkon topné spirály konvice
Skutečný příkon topné spirály konvice vypočítáme ze vztahu:
\[P\,=\,\frac{U^2}{R}\,,\]kde R je odpor topné spirály a U je skutečné napětí na spirále. Tyto veličiny jsme určili v minulém oddíle:
\[R\,=\,\frac{U_\mathrm{s}^2}{P_\mathrm{s}}\] \[U\,=\,\frac{U_0U_\mathrm{s}^2}{P_\mathrm{s}R_0+U_\mathrm{s}^2}\,.\]Obě rovnice dosadíme do vztahu pro skutečný příkon topné spirály:
\[P\,=\,\frac{U_0^2U_\mathrm{s}^4}{\left(P_\mathrm{s}R_0+U_\mathrm{s}^2\right)^2}\cdot\frac{P_\mathrm{s}}{U_\mathrm{s}^2}\,.\]Pro skutečný příkon topné spirály konvice tedy platí:
\[P\,=\,\frac{U_0^2U_\mathrm{s}^2P_\mathrm{s}}{\left(P_\mathrm{s}R_0+U_\mathrm{s}^2\right)^2}\,.\]Nyní vypočítáme číselnou hodnotu skutečného příkonu P:
U0 = 230 V, Ps = 2 000 W, Us = 230 V, R0 = 1,2 Ω
\[P\,=\,\frac{230^4{\cdot}2\,000}{\left(2\,000{\cdot}1{,}2+230^2\right)^2}\,\mathrm{W}\,=\,1\,830\,\mathrm{W}\,.\]Řešení části b): závislost příkonu na délce kabelu
V minulém oddíle jsme odvodili vztah pro skutečný příkon varné konvice:
\[P\,=\,\frac{U_0^2U_\mathrm{s}^2P_\mathrm{s}}{\left(P_\mathrm{s}R_0+U_\mathrm{s}^2\right)^2}.\tag{**}\]Při změně délky kabelu se mění i jeho odpor − odpor kovového vodiče je přímo úměrný jeho délce:
\[R\,=\,\rho\frac{l}{S}\,,\]kde ρ je měrný odpor vodiče (závisí na materiálu), l délka a S průřez vodiče.
Protože měrný odpor vodiče i jeho průřez jsou konstantní, platí pro odpor kabelu při délce l0:
\[R_0\,=\,\rho\frac{l_0}{S}\hspace{10px}\Rightarrow\hspace{10px}\frac{\rho}{S}\,=\,\frac{R_0}{l_0}\,.\]Odpor kovového vodiče tedy vypočítáme ze vztahu:
\[R\,=\,\frac{l}{l_0}R_0\,.\]Pokud chceme zkoumat závislost příkonu konvice na délce kabelu, musíme ve vzorci (**) nahradit odpor R0 odporem R, který je na délce kabelu závislý:
\[P\,=\,\frac{U_0^2U_\mathrm{s}^2P_\mathrm{s}}{\left(RP_\mathrm{s}+U_\mathrm{s}^2\right)^2}\,=\,\frac{U_0^2U_\mathrm{s}^2P_\mathrm{s}}{\left(\frac{R_0}{l_0}lP_\mathrm{s}+U_\mathrm{s}^2\right)^2}.\]Tento vztah ještě upravíme tak, abychom se zbavili složeného zlomku:
\[P\,=\,\frac{U_0^2U_\mathrm{s}^2P_\mathrm{s}}{\left(\frac{lR_0P_\mathrm{s}+U_\mathrm{s}^2l_0}{l_0}\right)^2}\,.\]A získáme tak příkon konvice jako funkci délky kabelu. Tato funkce je zadána předpisem:
\[P\,=\,\frac{U_0^2U_\mathrm{s}^2P_\mathrm{s}l_0^2}{\left(U_\mathrm{s}^2l_0+R_0P_\mathrm{s}\bf{l}\right)^2}\,.\]Jedná se o mocninnou funkci se záporným celočíselným exponentem -2. Argumentem funkce je délka kabelu l. Ta je v rovnici tučně zvýrazněna.
Ze zadání úlohy víme, že
U0 = 230 V, Ps = 2 000 W, Us = 230 V, l0 = 60 m, R0 = 1,2 Ω.
Nyní si pro l od 0 do 2 000 m sestavíme tabulku hodnot a nakreslíme graf závislosti příkonu konvice na délce kabelu:
l [m] 0 400 800 1 200 1 600 2 000 P [W] 2 000 1 179 776 550 410 317 Zde se kliknutím otevře excelovský soubor s daty.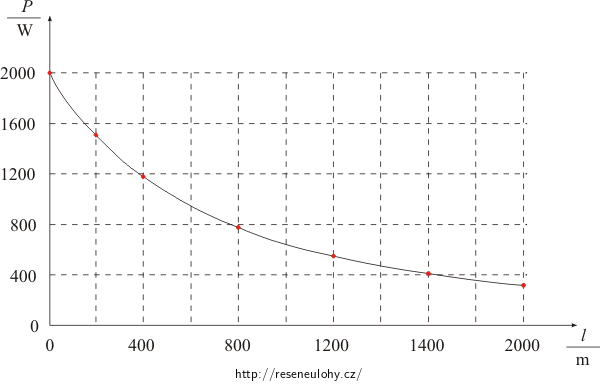
Odpověď k části a)
Skutečné napětí na topné spirále konvice je 220 V a její skutečný příkon je 1 830 W.







