Sbírka řešených úloh

Kapacitance sériového a paralelního zapojení kondenzátorů

Úloha číslo: 76

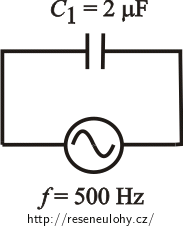
Kondenzátor o kapacitě 2 μF je připojen do obvodu střídavého proudu o frekvenci 500 Hz. Ke kondenzátoru připojíme další kondezátor o stejné kapacitě

a) paralelně,

b) sériově.

Jak musíme změnit frekvenci střídavého proudu, aby se kapacitance obvodu nezměnila?

 

• Zápis

  Ze zadání známe velikost kapacity kondenzátorů C₁, C₂ a velikost frekvence proudu na zdroji f:

  C₁ = C₂ = 2,0 μF = 2,0·10^-6 F,

  f = 500 Hz.

  Chceme vypočítat velikost frekvence proudu v obvodu tak, aby kapacitance obvodu zůstala po zapojení druhého kondenzátoru stejná:

  a) pro paralelní zapojení frekvenci označíme f_p = ? (Hz),

  b) pro sériové zapojení frekvenci označíme f_s = ? (Hz).

• Nápověda

  Vztah pro výpočet frekvence vyjádříme ze vztahu pro kapacitanci.

• Nápověda - Spojovaní kondenzátorů

  Mezi nábojem Q a napětím U na kondenzátoru platí vztah Q = CU, kde C je kapacita kondenzátoru.

  ---

  Paralelní zapojení:

  

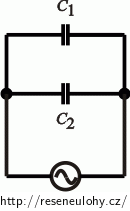
  Pro paralelní zapojení platí U₁ = U₂ = U a Q = Q₁ + Q₂:

  \[ C_\mathrm{p}=\frac{Q}{U}=\frac{Q_1+Q_2}{U}=\frac{Q_1}{U_1}+\frac{Q_2}{U_2} \] \[C_\mathrm{p}=C_1+C_2.\]

  ---

  Sériové zapojení:

  

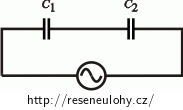
  Pro sériové zapojení platí pro napětí U = U₁ + U₂ a pro náboje platí Q = Q₁ = Q₂:

  \[ \frac{Q}{C_\mathrm{s}}=\frac{Q}{C_1}+\frac{Q}{C_2} \] \[ \frac{1}{C_\mathrm{s}}=\frac{1}{C_1}+\frac{1}{C_2} \] \[ C_\mathrm{s}=\frac{C_1 \, C_2}{C_1+C_2}. \]

• Rozbor úlohy

  Nejprve si vyjádříme celkové kapacity v paralelním i sériovém zapojení kondenzátorů. Pomocí celkových kapacit vypočteme novou kapacitanci v obvodu a porovnáním s původní kapacitancí vypočteme novou frekvenci proudu.

• Řešení

  Ze zadání víme, že kapacitance X_C má být pro sériové i paralelní zapojení druhého kondenzátoru C₂ stejná jako v obvodu, kde je zapojen jen kondenzátor C₁.

  Původní kapacitance obvodu:

  \[X_\mathrm{C}=\frac{1}{\omega C_1}=\frac{1}{2 \pi f C_1}.\]

  a) Kapacitance při paralelním zapojení:

  \[ X_\mathrm{C_p}=\frac{1}{\omega C_\mathrm{p}}=\frac{1}{2 \pi f_\mathrm{p} C_\mathrm{p}} .\]

  Dosadíme kapacity C₁, C₂ a využijeme toho, že C₁ = C₂:

  \[ X_\mathrm{C_p}=\frac{1}{2 \pi f_\mathrm{p}(C_1+C_2)}=\frac{1}{4 \pi f_\mathrm{p} C_1}. \]

  Porovnáme původní kapacitanci s kapacitancí pro paralelní zapojení kondenzátorů:

  \[X_\mathrm{C}=X_\mathrm{C_p}\] \[\frac{1}{2 \pi f C_1}=\frac{1}{4 \pi f_\mathrm{p} C_1}.\]

  Vyjádříme neznámou frekvenci f_p pro paralelní zapojení:

  \[\frac{1}{f}=\frac{1}{2 f_\mathrm{p}}\] \[f_\mathrm{p}=\frac{f}{2}.\]

  b) Kapacitance při sériovém zapojení:

  \[ X_\mathrm{C_s}=\frac{1}{\omega C_\mathrm{s}}=\frac{1}{2 \pi f_\mathrm{s} C_\mathrm{s}}. \]

  Dosadíme kapacity C₁, C₂ a využijeme toho, že C₁ = C₂:

  \[ X_\mathrm{C_s}=\frac{C_1+C_2}{2 \pi f_\mathrm{s}(C_1 C_2)}=\frac{2C_1}{2 \pi f_\mathrm{s} (C_1)^2}=\frac{1}{ \pi f_\mathrm{s} C_1}. \]

  Porovnáme původní kapacitu s kapacitou pro sériové zapojení kondenzátorů:

  \[X_\mathrm{C}=X_\mathrm{C_S}\]

  \[\frac{1}{2 \pi f C_1}=\frac{1}{ \pi f_\mathrm{s} C_1}.\]

  Vyjádříme neznámou frekvenci f_s pro sériové zapojení:

  \[\frac{1}{2f}=\frac{1}{ f_\mathrm{s}}\] \[f_\mathrm{s}=2f.\]

• Číselné dosazení

  a) Paralelní zapojení kondenzátorů:

  \[f_\mathrm{p}=\frac{f}{2}=\frac{500}{2} \, \mathrm{Hz}=250 \, \mathrm{Hz}. \]

  b) Sériové zapojení kondenzátorů:

  \[f_\mathrm{s}=2 f=2 {\cdot} 500 \, \mathrm{Hz} =1000\, \mathrm{Hz}. \]

• Odpověď

  Chceme-li po připojení druhého kondenzátoru C₂ o stejné kapacitě, jako má kondenzátor C₁, docílit stejně velké kapacitance, musíme změnit frekvenci v obvodu. Při paralelním připojení je potřeba frekvenci zmenšit na polovinu. Při sériovém připojení je potřeba frekvenci zvětšit na dvojnásobek.

  Paralelní zapojení: \(f_\mathrm{p}=250 \, \mathrm{Hz} \)

  Sériové zapojení: \(f_\mathrm{s}=1000 \, \mathrm{Hz} \)