Kondenzátor s komplexní impedancí
Úloha číslo: 493
Ideální kondenzátor o kapacitě 2,0 μF má při frekvenci f napětí zdroje komplexní impedanci \(\bar Z =(-1{,}6\, \mathrm{j})\,\mathrm k\Omega.\)
Určete:
a) velikost impedance,
b) frekvenci f napětí zdroje,
c) amplitudu proudu tekoucího kondenzátorem při dané frekvenci f a amplitudě napětí zdroje 50 V.
Pozn.: Komplexní jednotku budeme označovat j. Komplexní veličiny budeme značit pruhem.
Nápověda
Zopakujte si, co znáte o komplexní impedanci a o komplexních číslech. Nápovědy naleznete například v úloze Cívka s komplexní impedancí.
Nápověda — ideální kondenzátor
Máme-li v obvodu zařazený pouze ideální kondenzátor, znamená to, že velikost komplexní impedance kondenzátoru je rovna jeho kapacitanci.
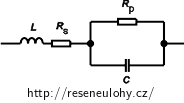
Pozn.: Náhradní schéma reálného kondenzátoru vedle hlavního prvku s kapacitou C zahrnuje rovněž parazitní sériový odpor Rs, parazitní indukci L (důsledky přípojného vedení) a parazitní paralelní odpor Rp (svod mezi elektrodami kondenzátoru). Impedance realného kondenzátoru je potom složena z impedancí všech prvků, které ho nahrazují, a je menší než u ideálního kondenzátoru.
Řešení a číselné dosazení
a) Velikost komplexní impedance \(\bar Z =(-1{,}6\, \mathrm{j})\,\mathrm k\Omega\) vypočteme jako:
\[Z = \sqrt{(- 1{,}6)^2}\,\mathrm {k\Omega} = 1{,}6\,\mathrm {k\Omega} .\]
b) Víme, že daný kondenzátor je ideální, což znamená, že velikost komplexní impedance bude stejná jako kapacitance kondenzátoru:
\[Z = X_\mathrm{C} .\]Frekvenci napětí zdroje pak získáme z kapacitance kondenzátoru:
\[ X_\mathrm{C} = \frac{1}{\omega C} = \frac{1}{2 \pi f C} .\]Dosadíme do předchozího vztahu a vyjádříme frekvenci f:
\[Z = \frac{1}{2 \pi f C} \] \[f = \frac{1}{2 \pi C Z} .\]Číselně dosadíme:
\[f = \frac{1}{2\cdot \pi \cdot 2{\cdot} 10^{-6} \cdot 1{,}6 {\cdot} 10^3} \,\dot=\, 50\, \mathrm {Hz}.\]
c) Amplitudu proudu tekoucího kondenzátorem při napětí 50 V získáme z Ohmova zákona:
\[I = \frac{U}{Z}=\frac{50}{1{,}6 {\cdot} 10^3 }\,\mathrm A \,\dot=\, 31 \,\mathrm {mA}.\]Nebo použijeme Ohmův zákon, do kterého dosadíme komplexní veličiny:
\[ \bar I = \frac{\bar U}{\bar Z} = \frac{ 50}{-1600\, \mathrm{j}}\,\mathrm A = \frac{ 50}{1600}\, \mathrm{j}\,\mathrm A \,\dot{=}\, 31\, \mathrm{j}\,\mathrm {mA}. \]Velikost komplexního proudu potom vyjadřuje hledanou amplitudu:
\[ I = |\bar Z| = \sqrt {31\, ^2}\,\mathrm mA=31\,\mathrm {mA}.\]Odpověď
Velikost impedance kondenzátoru je 1,6 kΩ, frekvence napětí zdroje je asi 50 Hz a velikost proudu tekoucího kondenzátorem při napětí 50 V je asi 31 mA.


