Zapojování reálných zdrojů

Úloha číslo: 2051

Určete elektromotorické napětí \(U_\mathrm{e}\) a vnitřní odpor \(R_\mathrm{i}\) zdroje, kterým bychom ekvivalentně nahradili zapojení dvou sériově, resp. paralelně zapojených baterií s parametry \(U_\mathrm{e1} = 1, 4\ \mathrm{V},\ R_\mathrm{i1} = 0{,}6 \ \Omega\) a \(U_\mathrm{e2} = 1, 2 \ \mathrm{V}, \ R_\mathrm{i2} = 0, 4 \ \Omega\).

Jaký proud poteče rezistorem o odporu \(R = 4, 2 \ \Omega\), připojíme-li ho na tento zdroj?

Nápověda
Uvědomte si, co je elektromotorické napětí, svorkové napětí a co je vnitřní odpor baterie.
Řešení nápovědy
Zdroj s vnitřním odporem si můžeme představit jako sériově zapojený ideální zdroj (bez vnitřního odporu) a rezistor s odporem rovným vnitřnímu odporu zdroje.

Pozn.: Pokud máme nějaký reálný zdroj (např. baterii), tak to, co je uvnitř červeného obdélníku, je schéma vnitřku baterie.

Elektromotorické napětí U_e je tzv. napětí na prázdno. Naměříme ho na svorkách zdroje, pokud není ke zdroji připojen žádný spotřebič, neboli zdrojem neteče žádný proud. (Uvědomte si, že voltmetr má opravdu obrovský odpor, a tedy proud protékající voltmetrem je zanedbatelně malý).

Svorkové napětí U_s se také měří na svorkách zdroje a to v případě, že ke zdroji je připojen nějaký spotřebič o odporu R. Po připojení spotřebiče ke zdroji začne obvodem téct proud a napětí, které naměří připojený voltmetr, klesne o úbytek napětí na vnitřním odporu zdroje. Svorkové napětí je tedy menší než elektromotorické napětí a jeho hodnota závisí i na protékajícím proudu.

Matematicky to můžeme vyjádřit pomocí tzv. zatěžovací charakteristiky zdroje
\[U_\mathrm{s} = U_\mathrm{e} - I R_\mathrm{i},\]
kde \(U_\mathrm{s}\) je svorkové napětí, \(U_\mathrm{e}\) je elektromotorické napětí, \(R_\mathrm{i}\) je vnitřní odpor zdroje a I je proud procházející obvodem.

Proud procházející spotřebičem o odporu R spočítáme pomocí Ohmova zákona pro část obvodu:
\[I=\frac{U_\mathrm{s}}{R}.\]
Vyjádříme svorkové napětí, dosadíme do zatěžovací charakteristiky a vyjádříme I:
\[RI = U_\mathrm{e} - I R_\mathrm{i},\] \[I = \frac{ U_\mathrm{e}}{R+ R_\mathrm{i}}.\]
Poslední vztah je tzv. Ohmův zákon pro uzavřený obvod.

Více o vnitřním odporu a zatěžovací charakteristice se můžete dočíst například na Encyklopedie fyziky .
Rozbor – sériově

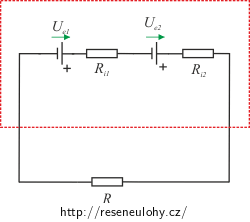
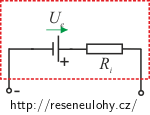
Pozn.: Červený rámeček ohraničuje „vnitřek“ zdroje.

Naším úkolem je nalézt parametry zdroje (elektromotorické napětí a vnitřní odpor), kterým bychom ekvivalentně nahradili tyto dvě sériově zapojené baterie. To znamená najít zdroj, který vykazuje stejné vlastnosti.

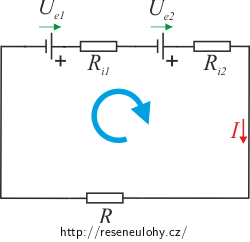
Napětí na sériově zapojených zdrojích, které mají stejnou orientaci, se sčítá. Podobně celkový odpor dvou sériově zapojených rezistorů je dán jejich součtem. Obojí je důsledkem 2. Kirchhoffova zákona. Proud procházející rezistorem spočteme pomocí Ohmova zákona.
Řešení – sériově
Jak bylo řečeno v rozboru, napětí na dvou sériově zapojených zdrojích spočteme jako jejich součet. Jedná se o důsledek 2. Kirchhoffova zákona, více je to rozebráno v oddílu níže, viz Výpočet pomocí Kirchhoffových zákonů .
\[U_\mathrm{e} = U_\mathrm{e1} + U_\mathrm{e2}.\]
Obdobně je to s vnitřním odporem. Jelikož jsou zdroje zapojeny sériově, jsou i vnitřní odpory zapojeny sériově. Celkový odpor dvou sériově zapojených rezistorů spočítáme jako jejich součet:
\[R_\mathrm{i} = R_\mathrm{i1} + R_\mathrm{i2}.\]
Proud procházející připojeným rezistorem o odporu \(R\) spočítáme podle Ohmova zákona pro uzavřený obvod
\[I = \frac {U_\mathrm{e}}{R+R_\mathrm{i}},\]
kde \(U_\mathrm{e}\) je celkové elektromotorické napětí a \(R_\mathrm{i}\) je celkový vnitřní odpor zdroje.

Celkový odpor zapojení spočítáme obdobně jako při výpočtu celkového vnitřního odporu, jelikož celkový vnitřní rezistor a připojený rezistor jsou v sérii.

Proud procházející připojeným rezistorem a tedy i celým obvodem je
\[I =\frac {U_\mathrm{e1} + U_\mathrm{e2}} {R_\mathrm{i1} + R_\mathrm{i2} + R}.\]
Výpočet pomocí Kirchhoffových zákonů

Znění Kirchhoffových zákonů.
Kuchařka pro použití Kirchhoffových zákonů.
Obvod nemá žádné uzly, proto je zřejmé, že celým obvodem teče stejný proud I.

Pro vyjádření proudu I využijeme druhého Kirchhoffova zákona:
\[U_\mathrm{e1} + U_\mathrm{e2} = R_\mathrm{i1}I + R_\mathrm{i2}I + R I,\] \[U_\mathrm{e1} + U_\mathrm{e2} = I (R_\mathrm{i1} + R_\mathrm{i2} + R),\] \[I= \frac{U_\mathrm{e1} + U_\mathrm{e2} } {R_\mathrm{i1} + R_\mathrm{i2} + R}.\]
Výsledek porovnáme s Ohmovým zákonem pro uzavřený obvod:
\[I= \frac{U_\mathrm{e}}{R+R_\mathrm{i}}.\]
Porovnáním získáme
\[U_\mathrm{e} =U_\mathrm{e1} + U_\mathrm{e2},\] \[R_\mathrm{i} =R_\mathrm{i1}+R_\mathrm{i2}. \]

Zápis a číselné dosazení – sériově

\(U_\mathrm{e1} = 1{,}4\ \mathrm{V}\)	elektromotorické napětí první baterie
\(R_\mathrm{i1}=0{,}6\ \Omega\)	vnitřní odpor první baterie
\(U_\mathrm{e2}=1{,}2\ \mathrm{V}\)	elektromotorické napětí druhé baterie
\(R_\mathrm{i1}=0{,}4\ \Omega\)	vnitřní odpor druhé baterie
\(R=4{,}2 \ \Omega\)	odpor připojeného rezistoru
\(I=\mathrm{?}\ \mathrm{(A)}\)	proud procházející rezistorem
\(U_\mathrm{e}=\mathrm{?}\ \mathrm{(V)} \)	celkové elektromotorické napětí zdroje
\(R_\mathrm{ic}=\mathrm{?}\ (\Omega) \)	celkový vnitřní odpor zdroje

\[U_\mathrm{e} =U_\mathrm{e1} + U_\mathrm{e2} =1{,}4 + 1{,}2\ \mathrm{V} = 2{,}6\ \mathrm{V}.\] \[R_\mathrm{ic} = R_\mathrm{i1}+R_\mathrm{i2}=0{,}6 + 0{,}4 \ \Omega = 1\ \Omega.\] \[I=\frac{U_\mathrm{e1} + U_\mathrm{e2}}{R_\mathrm{i1} + R_\mathrm{i2} + R}=\frac{1{,}4+1{,}2}{0{,}6+0{,}4+4{,}2}\ \mathrm{A}=0{,}5 \ \mathrm{A}.\]

Nápověda – paralelně
Nakreslete si obrázek vystihující zadání. Připomeňte si, jak zní a jak se používají Kirchhoffovy zákony. Jak by se daly Kirchhoffovy zákony použít v této úloze?
Řešení nápovědy
Situaci nám zachycuje následující obrázek.

Což si můžeme pro lepší názornost překreslit jako
Odkaz – Kirchhoffovy zákony a „kuchařka“ pro jejich použití
Znění Kirchhoffových zákonů.
Kuchařka pro použití Kirchhoffových zákonů.
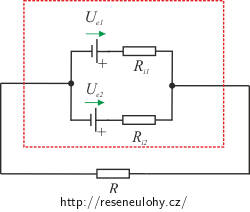
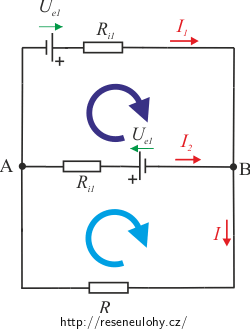
Rozbor – paralelně
Situaci si nakreslíme.

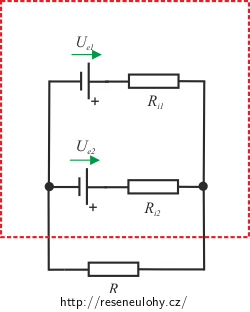
V obvodu máme zapojeno více zdrojů, proto použijeme k řešení Kirchhoffovy zákony. S jejich pomocí nalezneme vztah pro proud I procházející připojeným spotřebičem. Porovnáním získaného vztahu a Ohmova zákona pro uzavřený obvod určíme elektromotorické napětí a vnitřní odpor zdroje, který by ekvivalentně nahradil paralelně zapojené baterie.
Řešení – paralelně
\mathrm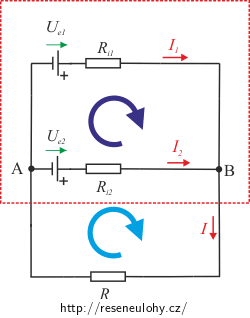

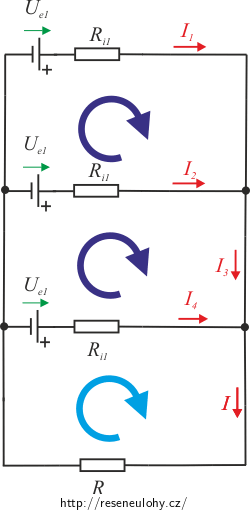
Dle prvního Kirchhoffova zákona si zapíšeme rovnice pro uzly A a B (jsou stejné, proto ji stačí napsat jen jednou):
\[I = I_1 + I_2.\tag{1}\]
Dle druhého Kirchhoffova zákona si zapíšeme rovnice pro jednotlivé smyčky.

Pozn.: Pozor na znaménkovou konvenci viz Kuchařka:
\[U_\mathrm{e1} - U_\mathrm{e2} = R_\mathrm{i1}I_1 - R_\mathrm{i2}I_2,\] \[U_\mathrm{e2} = R_\mathrm{i2}I_2 + RI.\]
Z rovnice (1) si vyjádříme \(I_1\) a dosadíme do soustavy:
\[U_\mathrm{e1} - U_\mathrm{e2} = R_\mathrm{i1}(I - I_2) - R_\mathrm{i2}I_2,\] \[U_\mathrm{e2} = R_\mathrm{i2}I_2 + RI.\]
Protože naším cílem je najít vztah pro I, vyjádříme z druhé rovnice \(I_2\):
\[U_\mathrm{e2} = R_\mathrm{i2}I_2 + RI\quad \rightarrow\quad I_2 = \frac{U_\mathrm{e2}-RI}{R_\mathrm{i2}}\]
a dosadíme do první rovnice:
\[U_\mathrm{e1} - U_\mathrm{e2} = R_\mathrm{i1}I - R_\mathrm{i1}\frac{U_\mathrm{e2}-RI}{R_\mathrm{i2}} - R_\mathrm{i2}\frac{U_\mathrm{e2}-RI}{R_\mathrm{i2}}.\]
Rovnici rozšíříme výrazem \(R_\mathrm{i2}\):
\[R_\mathrm{i2}(U_\mathrm{e1} - U_\mathrm{e2}) = R_\mathrm{i2}R_\mathrm{i1}I - R_\mathrm{i1}({U_\mathrm{e2}}-RI)- R_\mathrm{i2}(U_\mathrm{e2}-RI)\]
a vyjádříme \(I\):
\[I = \frac{R_\mathrm{i1}U_\mathrm{e2} + R_\mathrm{i2}U_\mathrm{e1} }{R_\mathrm{i1}R_\mathrm{i2} + R_\mathrm{i1}R + R_\mathrm{i2}R}.\]
Výsledek upravíme tak, aby byl podobný tvaru Ohmova zákona pro uzavřený obvod \(I=\frac{U_e}{R+R_i}\) (tj. chceme, aby jmenovatel zlomku měl tvar R + něco):
\[I = \frac{R_\mathrm{i1}U_\mathrm{e2} + R_\mathrm{i2}U_\mathrm{e1} }{R_\mathrm{i1}R_\mathrm{i2} + (R_\mathrm{i1} + R_\mathrm{i2})R} = \frac{R_\mathrm{i1}U_\mathrm{e2} + R_\mathrm{i2}U_\mathrm{e1}}{(R_\mathrm{i1} + R_\mathrm{i2})\left(\frac{R_\mathrm{i1}R_\mathrm{i2}}{R_\mathrm{i1} + R_\mathrm{i2}} + R\right)} = \frac{\frac{R_\mathrm{i1}U_\mathrm{e2} + R_\mathrm{i2}U_\mathrm{e1}}{R_\mathrm{i1} + R_\mathrm{i2}}}{R+\frac{R_\mathrm{i1}R_\mathrm{i2}}{R_\mathrm{i1} + R_\mathrm{i2}}}.\]
Porovnáním získáme
\[U_\mathrm{e} = \frac{R_\mathrm{i1}U_\mathrm{e2} + R_\mathrm{i2}U_\mathrm{e1}}{R_\mathrm{i1} + R_\mathrm{i2}}, \] \[R_\mathrm{i}=\frac{R_\mathrm{i1}R_\mathrm{i2}}{R_\mathrm{i1} + R_\mathrm{i2}}.\]

Zápis a číselné dosazení – paralelně

\(U_\mathrm{e1} = 1{,}4\ \mathrm{V}\)	elektromotorické napětí první baterie
\(R_\mathrm{i1}=0{,}6\ \Omega\)	vnitřní odpor první baterie
\(U_\mathrm{e2}=1{,}2\ \mathrm{V}\)	elektromotorické napětí druhé baterie
\(R_\mathrm{i1}=0{,}4\ \Omega\)	vnitřní odpor druhé baterie
\(R=4{,}2 \ \Omega\)	odpor připojeného rezistoru
\(I=\mathrm{?}\ \mathrm{(A)}\)	proud procházející rezistorem
\(U_\mathrm{e}=\mathrm{?}\ \mathrm{(V)} \)	celkové elektromotorické napětí zdroje
\(R_\mathrm{ic}=\mathrm{?}\ (\Omega) \)	celkový vnitřní odpor zdroje

\[R_\mathrm{ic}=\frac{R_\mathrm{i1}R_\mathrm{i2}}{R_\mathrm{i1}+R_\mathrm{i2}}=\frac {0{,}6{\cdot} 0{,}4}{0{,}6+0{,}4} \ \Omega = 0{,}24\ \Omega.\] \[I=\frac{R_\mathrm{i1}U_\mathrm{e2}+R_\mathrm{i2}U_\mathrm{e1}}{R_\mathrm{i1}R_\mathrm{i2}+R_\mathrm{i1}R+R_\mathrm{i2}R}=\frac{0{,}6{\cdot}1{,}2+ 0{,}4{\cdot} 1{,}4}{0{,}6{\cdot} 0{,}4+0{,}6{\cdot} 4{,}2 + 0{,}4{\cdot} 4{,}2}\ \mathrm{A}\doteq 0{,}29 \ \mathrm{A}.\] \[U_\mathrm{e} =\frac{R_\mathrm{i1}U_\mathrm{e2} + R_\mathrm{i2}U_\mathrm{e1}}{R_\mathrm{i1}+R_\mathrm{i2}} =\frac{1{,}4{\cdot} 0{,}4 + 1{,}2{\cdot} 0{,}6}{0{,}4 + 0{,}6}\ \mathrm{V} = 1{,}28\ \mathrm{V}.\]

Odpověď
Při sériovém zapojení má zdroj elektromotorické napětí \(U_\mathrm{e} = 2{,}6\ \mathrm{V}\) a vnitřní odpor \(R_\mathrm{i} = 1\ \Omega\). Připojeným rezistorem prochází proud \(I= 0{,}5\ \mathrm{A}.\)

Při paralelním zapojení má zdroj elektromotorické napětí \(U_\mathrm{e} = 1{,}28\ \mathrm{V}\) a vnitřní odpor \(R_\mathrm{i} =0{,}24\ \Omega.\) Připojeným rezistorem prochází proud \(I \doteq0{,}29\ \mathrm{A}.\)
Shrnutí a něco navíc
Celkový vnitřní odpor spočítáme z vnitřních odporů jednotlivých zdrojů. Můžeme si to představit tak, že v náhradním zapojení vynecháme ideální zdroje a spočítáme celkový odpor zapojení vnitřních odporů jednotlivých zdrojů.

Určit celkové elektromotorické napětí už tak jednoduché ale není. Při sériovém zapojení se elektromotorická napětí sčítají. Ale u paralelního zapojení nepočítáme pouze s elektromotorickými napětími jednotlivých zdrojů, ale ve výpočtu vystupuje také vnitřní odpor těchto zdrojů, protože je třeba započítat úbytky napětí na jednotlivých vnitřních odporech.
1) Paralelní zapojení dvou a více zdrojů
Paralelní zapojení dvou stejných zdrojů

Obecně jsme odvodili pro dva různé paralelně zapojené zdroje vztahy:
\[U_\mathrm{e} = \frac{R_\mathrm{i1}U_\mathrm{e2} + R_\mathrm{i2}U_\mathrm{e1}}{R_\mathrm{i1} + R_\mathrm{i2}}, \] \[R_\mathrm{i}=\frac{R_\mathrm{i1}R_\mathrm{i2}}{R_\mathrm{i1} + R_\mathrm{i2}}.\]
Máme-li dva stejné zdroje, pak \(R_\mathrm{i1}=R_\mathrm{i2}\) a \(U_\mathrm{e1}=U_\mathrm{e2}\):
\[U_\mathrm{e} = \frac{R_\mathrm{i1}U_\mathrm{e1} + R_\mathrm{i1}U_\mathrm{e1}}{R_\mathrm{i1} + R_\mathrm{i1}}=U_\mathrm{e1}. \] \[R_\mathrm{i}=\frac{R_\mathrm{i1}R_\mathrm{i1}}{R_\mathrm{i1} + R_\mathrm{i1}}=\frac{R_\mathrm{i1}}{2}.\]
Paralelní zapojení více stejných zdrojů

Stejně jako jsme odvodili vztah pro dva různé paralelně zapojené zdroje, odvodíme vztah pro tři stejné paralelně zapojené zdroje. Pro výpočet použijeme Kirchhoffových zákonů.

Dle prvního zákonu si zapíšeme rovnice pro jednotlivé uzly:
\[I_1 + I_2 = I_3,\] \[I_3 + I_4 = I.\]
Z čehož vyjádříme I:
\[I=I_1 + I_2 + I_4.\]
Dle druhého zákona si zapíšeme rovnice pro jednotlivé smyčky:
\[U_\mathrm{e1} - U_\mathrm{e1} = R_\mathrm{i1}I_1 - R_\mathrm{i1}I_2\] \[U_\mathrm{e1} - U_\mathrm{e1} = R_\mathrm{i1}I_2 - R_\mathrm{i1}I_4\] \[U_\mathrm{e1} = R_\mathrm{i1}I_4 + RI\]
____________________________
\[0 = R_\mathrm{i1}I_1 - R_\mathrm{i1}I_2\] \[0 = R_\mathrm{i1}I_2 - R_\mathrm{i1}I_4\] \[U_\mathrm{e1} = R_\mathrm{i1}I_4 + RI\]
____________________________
\[ R_\mathrm{i1}I_1 = R_\mathrm{i1}I_2 \implies I_1 = I_2\tag{*}\] \[ R_\mathrm{i1}I_2 = R_\mathrm{i1}I_4 \implies I_2 = I_4\tag{**}\] \[U_\mathrm{e1} = R_\mathrm{i1}I_4 + RI.\tag{***}\]
Nyní se vrátíme k rovnici, již jsme získali z prvního Kirchhoffova zákona:
\[I=I_1 + I_2 + I_4.\]
Do rovnice dosadíme (*) a (**):
\[I=3I_1 = 3I_2 = 3I_4,\] \[I_4 = \frac {I}{3}.\]
Poslední rovnost dosadíme do (***) a vyjádříme I:
\[U_\mathrm{e1} = R_\mathrm{i1}\frac {I}{3} + RI,\] \[U_\mathrm{e1} =I(\frac {R_\mathrm{i1}}{3} + R),\] \[I = \frac{U_{e1}}{\frac {R_\mathrm{i1}}{3} + R}.\]
Výsledek srovnáme s Ohmovým zákonem pro uzavřený obvod:
\[I= \frac {U_\mathrm{e}}{R_\mathrm{i} + R}.\]
Porovnáním získáme
\[U_\mathrm{e}= U_\mathrm{e1},\] \[R_\mathrm{i}\mathrm = \frac {R_\mathrm{i1}}{3}.\]
Je zřejmé, že pro n stejných paralelně zapojených zdrojů by výpočet probíhal stejně. Můžeme tedy napsat celkové elektromotorické napětí a celkový vnitřní odpor pro n stejných paralelně zapojených zdrojů:
\[U_\mathrm{e} = U_\mathrm{e1},\] \[R_\mathrm{i} = \frac {R_\mathrm{i1}}{n}.\]
2) Antiparalelní zapojení dvou stejných zdrojů

Z předchozích výpočtů víme, že máme-li dva paralelně zapojené zdroje o elektromotorickém napětí \(U_\mathrm{e1}\) a \(U_\mathrm{e2}\) s vnitřními odpory \(R_\mathrm{i1}\) a \(R_\mathrm{i2}\), pak pro celkové elektromotrické napětí a celkový odpor platí
\[U_\mathrm{e} = \frac{R_\mathrm{i1}U_\mathrm{e1} + R_\mathrm{i1}U_\mathrm{e1}}{R_\mathrm{i1} + R_\mathrm{i1}}, \] \[R_\mathrm{i}=\frac{R_\mathrm{i1}R_\mathrm{i1}}{R_\mathrm{i1} + R_\mathrm{i1}}.\]
Máme-li zapojené dva zdroje antiparalelně, pak \(U_\mathrm{e1}=-U_\mathrm{e2}\) a \(R_\mathrm{i1} =R_\mathrm{i2}. \) Po dosazení dostaneme
\[U_\mathrm{e} = 0\ \mathrm{ V}. \] \[R_\mathrm{i}=\frac{R_\mathrm{i1}}{2}.\]
Zde je důležité si uvědomit, že i když na zdroj připojím rezistor (stejně tak, když ho nepřipojím) o odporu \(R\), tak proud poteče pouze smyčkou se zdroji („uvnitř baterie“), velikost tohoto proudu bude \(I_\mathrm{B}=\frac{U_\mathrm{e1}}{R_\mathrm{i1}} \) a baterie se bude rychle vybíjet. Připojeným rezistorem nepoteče proud, protože celkové elektromotorické napětí zdroje je nulové (body A a B mají stejný potenciál).
Odkaz – n paralelních zdrojů metodou lineární superpozice
Na tuto úlohu navazuje úloha Paralelní zapojení reálných zdrojů.