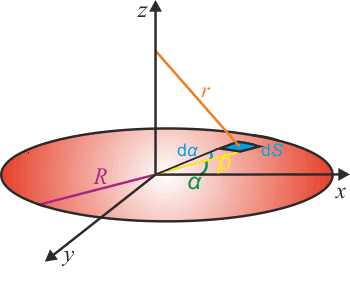
Nabitá kruhová deska
Úloha číslo: 2007
Nápověda – elektrická intenzita
Kladný bodový náboj Q vytváří ve vzdálenosti r pole o intenzitě
\[E=\frac{1}{4\pi\epsilon_0} \frac{Q}{r^2}.\]Vektor intenzity \(\vec{E}\) míří směrem od náboje, pokud je Q kladný. V opačném případě míří k náboji.
Zamyslete se nad tím, jak bychom tohoto poznatku mohli využít v této úloze.
Řešení – elektrická intenzita
Bodový náboj Q vytváří ve vzdálenosti r pole o intenzitě
\[{E}=\frac{1}{4\pi\epsilon_0} \frac{Q}{r^2}.\]Velikost elektrické intenzity od nekonečné malé plošky dS je
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0}\frac{\mathrm{d}Q}{r^2}.\]Je-li disk nabit nábojem s plošnou hustotou \(\sigma\), potom náboj na nekonečně malém kousku disku \(\textrm{d}S\) je
\[\textrm{d}Q = {\sigma} {\textrm{d}S},\]kde \(\textrm{d}S=\rho\,\textrm{d}\alpha\,\textrm{d}\rho\) (viz předchozí oddíl).
Potom dostáváme
\[\textrm{d}Q=\sigma \rho \textrm{d}\alpha\textrm{d}\rho\]a tudíž
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0}\frac{\sigma \rho\textrm{d}\alpha\textrm{d}\rho}{r^2}.\tag{1}\]Bez újmy na obecnosti můžeme předpokládat, že disk je nabit kladně. Nyní se zaměříme na směr intenzity. Stejně jako v úloze Nabitá obruč využijeme souměrnosti disku.
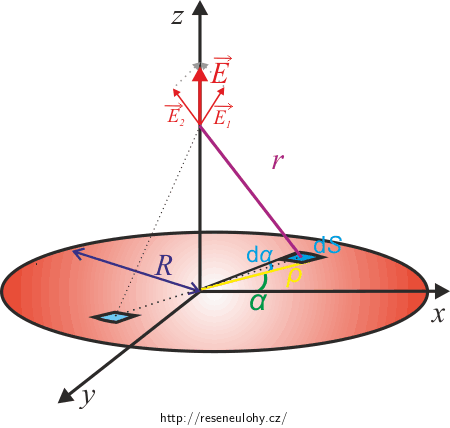
Z obrázku je patrné, že směr celkové intenzity elektrického pole bude mít směr osy z, jelikož x–ová složka elektrické intenzity od plošky disku se odečte s x–ovou složkou elektrické intenzity plošky, která je symetrická (středově souměrná) s touto ploškou podle středu disku. Stejně tak bude y–ová složka celkové intenzity také nulová.
Nyní se vrátíme k rovnici (1).
V obrázku si označíme úhel \(\omega\) a elektrickou intenzitu od jedné malé plošky promítneme do směru z, neboli vyjádříme její z–ovou složku:
\[E_\mathrm{z}=E \cos \omega.\tag{2}\]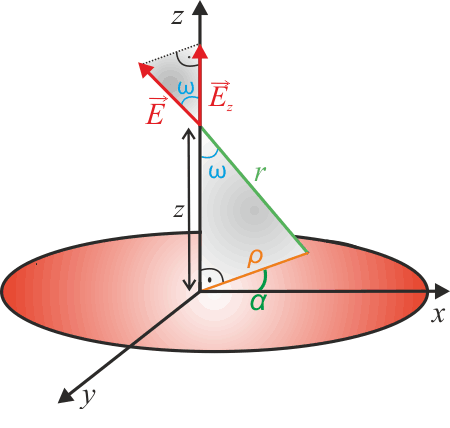
Z pravoúhlosti spodního šedého trojúhelníku dostaneme
\[\cos \omega = \frac {z}{r}\]a Pythagorova věta nám k tomu přidá
\[r=\sqrt{\rho^2 + z^2},\]což nám dává
\[\cos \omega = \frac {z}{\sqrt{\rho^2 + z^2}}.\tag{3}\]Spojením (1),(2) a (3) dostaneme
\[\textrm{d}{E_\mathrm{z}}=\frac{1}{4\pi\epsilon_0}\frac{\sigma\rho \textrm{d}\alpha\textrm{d}\rho}{\rho^2 + z^2}\frac {z}{\sqrt{\rho^2 + z^2}},\] \[\textrm{d}E_\mathrm{z} = \frac {\sigma z}{4\pi\epsilon_0} \frac {\rho} {(\rho^2 + z^2)^{3/2}} \textrm{d}\alpha \textrm{d}\rho,\]což zintegrujeme přes obsah celého disku, tj. budeme integrovat přes \(\rho\) a \(\alpha\):
\[E_\mathrm{z} = \int_0^{R} \int_0^{2\pi} \frac {\sigma z}{4\pi\epsilon_0} \frac {\rho} {(\rho^2 + z^2)^{3/2}} \textrm{d}\alpha \textrm{d}\rho.\]Veličiny \(\sigma\) a z jsou nezávislé na integračních proměnných \( \rho \) a \(\alpha,\) tudíž je můžeme vytknout před integrál:
\[E_\mathrm{z} = \frac {\sigma z}{4\pi\epsilon_0} \int_0^{R} \int_0^{2\pi} \frac {\rho} {(\rho^2 + z^2)^{3/2}}\textrm{d}\alpha \textrm{d}\rho .\]Nyní výraz zintegrujeme přes proměnou \(\alpha\), jelikož se ve výrazu \(\alpha\) nevyskytuje, integrujeme vlastně konstantu:
\[E_\mathrm{z} =\frac {\sigma z}{4\pi\epsilon_0} 2\pi \int_0^{R} \frac {\rho} {(\rho^2 + z^2)^{3/2}}\textrm{d}\rho,\] \[E_\mathrm{z} = \frac {\sigma z}{2\epsilon_0} \int_0^{R} \frac {\rho} {(\rho^2 + z^2)^{3/2}}\textrm{d}\rho.\]Tento integrál budeme řešit substitucí:
\[a = \rho^2 + z^2,\] \[\textrm{d}a = 2\rho\textrm{d}\rho, \]přepočítáme meze:
\[\rho = 0 \Rightarrow a = z^2;\qquad \rho = R \Rightarrow a = z^2 + R^2 \]a dosadíme do původního integrálu:
\[E_\mathrm{z} = \frac {\sigma z}{2\epsilon_0} \int_{z^2}^{z^2 + R^2} \frac {1} {2a^{3/2}}\textrm{d}a,\] \[E_\mathrm{z} = \frac {\sigma z}{4\epsilon_0} \int_{z^2}^{z^2 + R^2} {a^{-3/2}}\textrm{d}a,\] \[E_\mathrm{z} = \frac {\sigma z}{4\epsilon_0} \left[-2a^{-1/2}\right]_{z^2}^{z^2 + R^2}, \tag{*}\] \[E_\mathrm{z} = - \frac {\sigma}{2\epsilon_0} \frac{z}{\sqrt{z^2 + R^2}} + \frac {\sigma}{2\epsilon_0}. \]Po úpravě dostáváme
\[E_\mathrm{z} = \frac {\sigma} {2\epsilon_0} \left(1-\frac {z} {\sqrt{R^2 + z^2}}\right). \]Vzdálenost z bereme jako kladnou, proto ještě doplníme absolutní hodnotu:
\[E_\mathrm{z} = \frac {\sigma} {2\epsilon_0} \left(1-\frac {|z|} {\sqrt{R^2 + z^2}}\right). \]Nápověda – potenciál
Analogicky jako v části a) využijeme vztah pro potenciál bodového náboje. Potenciál bodového náboje ve vzdálenosti r je
\[φ = \frac {1}{4\pi\epsilon_0} \frac {Q}{r}.\]Vymyslete, jak vztah využít pro výpočet potenciálu na ose nabitého disku.
Řešení – potenciál
Bodový náboj Q vytváří ve vzdálenosti r potenciál
\[\varphi = \frac{1}{4\pi\epsilon_0} \frac{Q}{R}.\]Zaměříme-li se na malou plošku disku dS s nábojem dQ, pak potenciál d\(\varphi\) od této plošky je
\[\textrm{d}\varphi = \frac{1}{4\pi\epsilon_0} \frac {\textrm{d}Q}{r}. \tag{4}\]Jelikož je disk nabit plošnou hustotou \(\sigma\), můžeme napsat
\[\textrm{d}Q=\sigma\textrm{d}S.\]Díky poznatku \(\textrm{d}S = \rho\,\textrm{d}\alpha\thinspace\textrm{d}\rho\) (viz Rozbor – elektrická intenzita – obsah nekonečně malé plošky) dostaneme
\[\textrm{d}Q = \sigma \rho\,\textrm{d}\alpha\thinspace\textrm{d}\rho.\tag{5}\] \[\textrm{d}\varphi = \frac{1}{4\pi\epsilon_0} \frac {\sigma \rho}{r}\textrm{d}\alpha\thinspace\textrm{d}\rho.\tag{6}\]Nyní se zaměříme na vyjádření vzdálenosti r pomocí parametrů disku a vzdálenosti z.
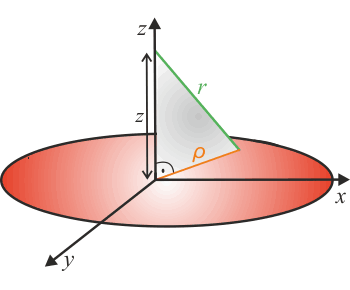
Aplikujeme Pythagorovu větu na pravoúhlý trojúhelník na obrázku a vyjádříme r:
\[r=\sqrt{\rho^2 + z^2}.\tag{7}\]Spojením (6) a (7) získáme rovnici
\[\textrm{d}\varphi = \frac{1}{4\pi\epsilon_0} \frac {\sigma \rho}{\sqrt{\rho^2 + z^2}}\textrm{d}\alpha\thinspace\textrm{d}\rho,\]což zintegrujeme přes celý obsah disku, tj. budeme integrovat přes \(\rho\) a \(\alpha\):
\[\varphi =\int_0^{2\pi}\int_0^{R} \frac{1}{4\pi\epsilon_0} \frac {\sigma \rho}{\sqrt{\rho^2 + z^2}}\textrm{d}\rho\,\textrm{d}\alpha.\]K a \(\sigma\) jsou konstanty, tudíž je můžeme vytknout před integrál:
\[\varphi =\frac{1}{4\pi\epsilon_0}\sigma\int_0^{2\pi}\int_0^{R} \frac {\rho}{\sqrt{\rho^2 + z^2}}\textrm{d}\rho\,\textrm{d}\alpha.\]Integrovaná funkce není závislá na \(\alpha\), proto můžeme přes \(\alpha\) jednoduše vyintegrovat:
\[\varphi =\frac{1}{4\pi\epsilon_0}2\pi\sigma\int_0^{R} \frac {\rho}{\sqrt{\rho^2 + z^2}}\textrm{d}\rho,\] \[\varphi =\frac{\sigma}{2\epsilon_0}\int_0^{R} \frac {\rho}{\sqrt{\rho^2 + z^2}}\textrm{d}\rho.\]Na vyřešení tohoto integrálu použijeme stejnou substituci jako v části a)
\[a = \rho^2 + z^2.\]Dosadíme
\[ \textrm{d}a = 2\rho\textrm{d}\rho, \] \[\rho = 0 \Rightarrow a = z^2 \qquad; \qquad \rho = R \Rightarrow a = R^2 + z ^2,\] \[\varphi =\frac{\sigma}{2\epsilon_0}\int_{z^2}^{R^2+z^2} \frac {1}{2}\frac {1}{\sqrt{a}}\textrm{d}a,\] \[\varphi =\frac{\sigma}{2\epsilon_0}\int_{z^2}^{R^2+z^2} \frac {1}{2}a^{-\frac {1}{2}}\textrm{d}a\]a spočteme
\[\varphi =\frac{\sigma}{2\epsilon_0} \left[a^{\frac{1}{2}}\right]_{z^2}^{z^2 + R^2},\tag{**}\] \[\varphi =\frac {\sigma} {2\epsilon_0} \left(\sqrt{z^2 + R^2} - z\right).\]Vzdálenost z bereme jako kladnou, proto ještě doplníme absolutní hodnotu:
\[\varphi =\frac {\sigma} {2\epsilon_0} \left(\sqrt{z^2 + R^2} - |z|\right).\]Nápověda – ověření vztahu mezi potenciálem a elektrickou intenzitou
Potenciál a elektrickou intenzitu nám dává do vztahu jedna z rovností, ve které vystupuje matematický operátor gradient.
Zkuste si vzpomenout, popřípadě najít o jaký vztah se jedná. Připomeňte si, co gradient znamená a jak se počítá (v kartézských souřadnicích).
Řešení – ověření vztahu mezi potenciálem a elektrickou intenzitou
Máme ověřit, zda platí vztah zmíněný v řešení předešlé nápovědy:
\[\vec{E}=-\thinspace\text{grad}\thinspace\varphi.\]Ověření můžeme provést jen pro body na ose obruče a jen pro z–ovou složku, protože v části b) jsme určili pouze potenciál na ose z:
\[\frac{\partial{\varphi}}{\partial{z}}=-\frac{\sigma}{2\epsilon_0}\left(\frac{1}{2}(z^2+R^2)^{-\frac{1}{2}}2z - 1 \right).\]Tedy
\[E_\mathrm{z}=\frac{\sigma}{2\epsilon_0}\left(1-\frac{z}{\sqrt{z^2+R^2}} \right),\]což souhlasí s výpočtem.
Nyní ještě ověříme, zda platí obrácený vztah
\[\varphi=-\int_\infty^{\hat {z}}{E_\mathrm{z}}\textrm{d}z,\]kde integrujeme podél osy \(z\) z „nekonečna“, kde je potenciál roven nule, do místa se souřadnicí \(\hat {z}\). Protože intenzita má směr osy, můžeme použít vztah \(\vec{E}\cdot\mathrm{d}\vec{r} = E_\mathrm{z}\,\mathrm{d}z\). Dosadíme-li vztah pro \(E_\mathrm{z}\) z části a), dostaneme
\[\varphi=-\int_\infty^{{\hat {z}}}\frac {\sigma} {2\epsilon_0} \left(1-\frac {z} {\sqrt{R^2 + z^2}}\right)\textrm{d}z,\] \[\varphi=-\frac {\sigma} {2\epsilon_0}\int_\infty^{{\hat {z}}} \left(1-\frac {z} {\sqrt{R^2 + z^2}}\right)\textrm{d}z,\] \[\varphi=-\frac {\sigma} {2\epsilon_0} \left(\left[\frac {z}{1}\right]_\infty^{{\hat {z}}}-\int_\infty^{\hat {z}}\frac {z} {\sqrt{R^2 + z^2}}\textrm{d}z\right).\]Zbývající integrál budeme řešit pomocí stejné substituce jako v předchozích částech:
\[R^2 + z^2 = a,\] \[2z \textrm{d}z = \textrm{d}a,\] \[z \rightarrow \infty \Rightarrow a \rightarrow \infty \qquad; \qquad z = \hat {z} \Rightarrow a = \hat {z}^2 + R^2,\] \[\varphi=-\frac {\sigma} {2\epsilon_0} \left(\left[z\right]_\infty^{\hat {z}}-\int_\infty^{\hat {z}^2 + {R^2}}\frac {1} {2a^{1/2}}\textrm{d}a\right),\] \[\varphi=-\frac {\sigma} {2\epsilon_0} \left(\left[z\right]_\infty^{{\hat {z}}}-\int_\infty^{\hat {z}^2 + \mathrm{R^2}}\frac {1} {2}a^{-1/2}\textrm{d}a\right),\] \[\varphi=-\frac {\sigma} {2\epsilon_0}\left(\left[z\right]_\infty^{{\hat {z}}}-\left[\frac{1}{2}\frac {a^{1/2}}{\frac{1}{2}}\right]_\infty^{{\hat {z}^2 + R^2}}\right).\tag{8}\]Hodnotu integrálu nemůžeme dopočítat, jelikož dostáváme neurčitý výraz \(\infty - \infty\). Příčinou potíží bylo rozdělení původního integrálu na dva. Z toho důvodu spočítáme původní integrál nejprve jako neurčitý a teprve potom dosadíme meze do výsledného výrazu.
Integrál nebudeme počítat celý znovu, využijeme toho, co jsme již spočítali. Odstraníme–li z výrazu (8) meze a dosadíme–li do výsledku použitou substituci \(a = R^2 + z^2\), máme neurčitý integrál spočítaný:
\[-\int\frac {\sigma} {2\epsilon_0} \left(1-\frac {z} {\sqrt{R^2 + z^2}}\right)\textrm{d}z=-\frac {\sigma} {2\epsilon_0}\left(z-(R^2 + z^2)^{1/2}\right)\thinspace+\thinspace\mathrm{konstanta}.\]Do něj teď doplníme meze:
\[\varphi = -\int_\infty^{\hat {z}}\frac {\sigma} {2\epsilon_0} \left(1-\frac {z} {\sqrt{R^2 + z^2}}\right)\textrm{d}z= -\frac {\sigma} {2\epsilon_0}\Big[z-\sqrt{(R^2 + z^2)}\Big]_\infty^{\hat {z}}.\]Horní mez lze dosadit bez potíží, dosazení spodní (nevlastní) meze znamená spočítat limitu
\[\lim_{z\rightarrow \infty} z-\sqrt{(R^2 + z^2)} =, \]kterou rozšíříme výrazem \(z + \sqrt{R^2 + z^2} \) a dostaneme
\[= \lim_{z\rightarrow \infty} \frac {z^2 -(R^2 + z^2)}{z + \sqrt{R^2 + z^2}}= \lim_{z\rightarrow \infty} \frac {-R^2}{z + \sqrt{R^2 + z^2}} = 0.\]Výsledkem dosazení mezí je výraz
\[\varphi = -\frac {\sigma} {2\epsilon_0} (\hat {z} - \sqrt{R^2 + \hat{z}^2} - 0) = \frac {\sigma} {2\epsilon_0} (\sqrt{R^2 + \hat {z}^2} - \hat {z}).\]Jelikož \(\hat {z}\) je libovolný bod na ose z, můžeme přeznačit jeho souřadnici na \(z\):
\[\varphi= \frac {\sigma} {2\epsilon_0} (\sqrt{R^2 + {z}^2} - {z}),\]čímž dostaneme očekávaný výraz.
Grafy průběhu elektrické intenzity a potenciálu
Na následujících obrázcích si můžeme prohlédnout závislosti elektrické intenzity a potenciálu na vzdálenosti z od středu disku.
Pozn. při vykreslování grafů je z bráno jako kladné, jelikož jde o vzdálenost.
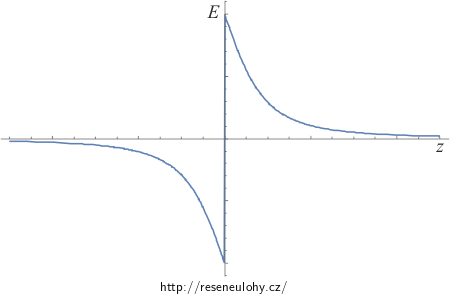
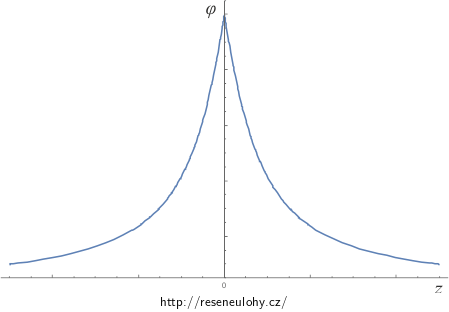
Pro \(z = 0\) procházíme nabitou plochou. Potenciál je spojitý, kdežto elektrická intenzita má v tomto bodě skok, jehož velikost je \(\frac {\sigma}{\varepsilon_0} \), což je v souladu s teorií.
Komentář – alternativní řešení s využitím úlohy o obruči
Elektrickou intenzitu a potenciál na ose z homogenně nabitého disku můžeme také najít o něco rychleji s využitím výsledků úlohy Nabitá obruč.
Na ose homogenně nabité obruče o poloměru R je ve vzdálenosti z potenciál (viz Nabitá obruč, Řešení b))
\[\varphi=\frac {1}{2\epsilon_0} \frac {\lambda R}{\sqrt{R^2 + z^2}}\]a elektrická intenzita (viz Nabitá obruč, Řešení a))
\[E_\mathrm{z} =\frac{\lambda R}{2\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}}. \]Začneme potenciálem \(\varphi\). Představíme si disk jako mnoho „velmi tenkých“ (nekonečně tenkých) obručí naskládaných do sebe. Poloměr této obruče označíme \(\rho\) a její tloušťku \(\mathrm{d}\rho\). Vztah mezi plošnou hustotou náboje disku \(\sigma\) a délkovou hustotou náboje \(\lambda\) nalezneme třeba pomocí vyjádření celkového náboje jedné obruče: \[Q = \lambda\cdot\mathrm{délka\ obruče} = \sigma \cdot\mathrm{plocha\ obruče} \quad\Rightarrow\quad \lambda\,2\pi\rho = \sigma2\pi\rho\mathrm{d}\rho \quad\Rightarrow\quad\lambda=\sigma\mathrm{d}\rho.\] Pak můžeme napsat, že příspěvek k potenciálu \(\textrm{d}\varphi\) od jedné nekonečně tenké obruče o poloměru ρ je
\[\textrm{d}\varphi=\frac {1}{2\epsilon_0} \frac {\sigma\rho}{\sqrt{\rho^2 + z^2}}\textrm{d}\rho.\]Zintegrujeme-li tento výraz přes celý disk (nasčítáme příspěvky od každé z obručí, což můžeme, jelikož je potenciál skalární veličina), dostaneme vztah pro potenciál homogenně nabitého disku:
\[\varphi= \int_0^{R}\frac {1}{2\epsilon_0} \frac {\sigma\rho}{\sqrt{\rho^2 + z^2}}\textrm{d}\rho.\]Po zintegrování (využijeme stejnou substituci jako v předešlých oddílech) dostaneme
\[\varphi = \frac{\sigma}{2\epsilon_0}\Big(\sqrt{R^2 + z^2} - z \Big).\]Nyní se zaměříme na velikost elektrické intenzity E. Již víme, že výsledný směr elektrické intenzity na ose obruče míří ve směru její osy. Stejně jako při výpočtu potenciálu si pomyslně „rozřežeme“ disk na jednotlivé obruče. Jednotlivé příspěvky k elektrické intenzitě od každé obruče můžeme nasčítat (naintegrovat), jelikož mají všechny stejný směr (směr osy obruče).
Příspěvek k elektrické intenzitě \(\textrm{d}E_\mathrm{z}\) od jedné nekonečně tenké obruče o poloměru \(\rho\) bude
\[\textrm{d}E_\mathrm{z} =\frac{\lambda \rho}{2\epsilon_0} \frac {z} {\sqrt{(z^2 + \rho^2)^3}}\textrm{d}\rho. \]Zintegrujeme-li (opět stejná substituce) tento výraz přes celý disk, dostaneme vztah pro elektrickou intenzitu homogenně nabitého disku
\[E_\mathrm{z} =\int_0^{R}\frac{\lambda \rho}{2\epsilon_0} \frac {z} {\sqrt{(z^2 + \rho^2)^3}}\textrm{d}\rho =\frac{\sigma}{2\epsilon_0}\Big( 1 - \frac {z} {\sqrt{(z^2 + R^2)}} \Big). \]Odpověď
Elektrická intenzita na ose homogenně nabitého disku na směr osy \(z\) a velikost \[E = \frac {\sigma} {2\epsilon_0} \left(1-\frac {|z|} {\sqrt{R^2 + z^2}}\right). \] Potenciál na ose homogenně nabitého disku je \[\varphi =\frac {\sigma} {2\epsilon_0} \left(\sqrt{z^2 + R^2} - |z|\right).\]Dále jsme pro body na ose obruče ověřili platnost vztahu mezi \(\vec {E}\) a \(\varphi\).
Limitní přechod k nabité ploše
Nyní zkusme uvažovat nekonečný poloměr disku. Vznikne homogenně nabitá rovina. Využijme dosavadních výpočtů pro určení intenzity a potenciálu ve vzdálenost z, nad touto plochou.
Intenzita v okolí homogenně nabité rovinyZ předchozích výpočtů využijeme (viz (*))
\[E_\mathrm{z} = \frac {\sigma z}{4\epsilon_0} \left[-2a^{-1/2}\right]_{z^2}^{z^2 + R^2}. \]Pokud \(R \rightarrow \infty \), pak
\[E_\mathrm{z} = \frac {\sigma z}{4\epsilon_0} \left[-2a^{-1/2}\right]_{z^2}^{\infty} = -\frac {\sigma z}{4\epsilon_0}\left[\frac{2}{\sqrt{a}}\right]_{z^2}^{\infty} = -\frac {\sigma z}{4\epsilon_0}\left(0 - \frac {2} {z}\right) = \frac{\sigma}{2\epsilon_0} . \] Potenciál homogenně nabité rovinyZ předchozích výpočtů využijeme (viz (**))
\[\varphi =\frac{\sigma}{2\epsilon_0} \left[a^{\frac{1}{2}}\right]_{z^2}^{z^2 + R^2}.\]Pokud \(R \rightarrow \infty \), pak
\[\varphi =\frac{\sigma}{2\epsilon_0} \left[a^{\frac{1}{2}}\right]_{z^2}^{\infty} = \frac{\sigma}{2\epsilon_0} (\infty - z) = \infty .\]Po dosazení mezí nám vychází potenciál nekonečný, protože výpočet potenciálu předpokládá nulový potenciál v nekonečnu, ale nám do nekonečna zasahuje nabitá plocha. Abychom se potenciálu dopočítali, museli bychom zvolit jiný postup výpočtu. Zde se omezíme pouze na odkaz na úlohu, kde je potenciál rovnoměrně nabité roviny počítán Pole rovnoměrně nabité roviny.
Dynamický prvek
V apletu jsou zobrazeny tři grafy průběhu elektrické intenzity.
- Modrý je graf průběhu elektrické intenzity disku, kterou jsme spočítali v úloze výše. V apletu můžeme nastavovat poloměr tohoto disku (plošná hustota elektrického náboje se nemění).
- Červený je graf průběhu elektrické intenzity bodového náboje umístěného ve středu disku se stejnou velikostí, jako je celkový náboj na disku.
- Černý je graf průběhu elektrické intenzity nabité roviny, která má stejnou plošnou hustotu náboje jako disk.
Úlohy pro práci s aplety
- Uveďte aplet do základního nastavení (RESET) a zmenšujte poloměr (nejlépe tak, že posuvník označíte myší a pak použijete kurzorové šipky). Pozorujte, jak se graf průběhu elektrické intenzity disku blíží ke grafu průběhu elektrické intenzity bodového náboje. Vysvětlete, proč grafy splývají?
- Zvětšujte poloměr disku a pozorujte, jak se graf průběhu elektrické intenzity disku blíží ke grafu průběhu elektrické intenzity nabité plochy. Vysvětlete, proč grafy splývají?