Měděný drát
Úloha číslo: 319
a) Najděte hustotu volných elektronů v kusu mědi, jestliže každý atom přispívá jedním elektronem.
b) Vypočtěte průměrnou rychlost uspořádaného pohybu elektronů v měděném drátu s průměrem 1 mm a vedoucím proud 1 A. Vysvětlete, jak je možné, že při tak „hlemýždí“ hodnotě se vůbec někdy rozsvítí žárovka.
c) Jaká je přitažlivá magnetická síla mezi dvěma takovými dráty, které jsou vzdáleny 1 cm od sebe?
d) Pokud bychom nějakým způsobem mohli odstranit kladné ionty z mřížky mědi (a zbyly pouze volné elektrony), jak velká by byla elektrická odpudivá síla drátů? Kolikrát by byla větší než síla magnetická?
Pozn.: V části c) a d) zanedbejte průměr měděného drátu vzhledem ke vzdálenosti obou drátů. Dále předpokládejte, že oba dráty jsou velmi dlouhé, takže je můžeme považovat za nekonečné. Obě síly počítejte na jednotku délky.
Zápis
d = 1 mm průměr měděného drátu I = 1 A proud tekoucí měděným drátem x = 1 cm vzdálenost dvou měděných drátů σ = ? (m-3) hustota volných elektronů v kusu mědi v = ? (m s-1) průměrná rychlost elektronů v měděném drátu Fm = ? (N) magnetická přitažlivá síla mezi dvěma měděnými dráty Fe = ? (N) elektrická odpudivá síla Z tabulek: e = 1,60·10-19 C náboj volného elektronu ρ = 8,96 g cm-3 hustota mědi NA = 6,02·1023 mol-1 Avogadrova konstanta Mm = 63,54 g mol-1 molární hmotnost mědi µ0 = 4π·10-7 H m-1 permeabilita vakua (resp. vzduchu) ε0 = 8,85·10-12 F m-1 permitivita vakua (resp. vzduchu) a) Nápověda
Potřebujeme zjistit počet, resp. hustotu volných elektronů, která bude stejná jako počet (resp. hustota) atomů v mědi. K tomu použijte veličiny molekulové fyziky.
a) Rozbor
Hustota volných elektronů v kusu mědi se rovná podílu počtu volných elektronů a objemu tohoto kusu mědi.
Abychom mohli hustotu volných elektronů dopočítat číselně, musíme si počet volných elektronů a objem mědi vyjádřit pomocí fyzikálních veličin, jejichž hodnotu můžeme nalézt ve fyzikálních tabulkách. K tomu využijeme i veličiny molekulové fyziky:
1. Objem kusu mědi vyjádříme podílem hmotnosti kusu mědi a hustoty mědi.
2. Každý atom v kusu mědi přispívá jedním volným elektronem. Počet volných elektronů je tedy stejný jako počet atomů v mědi.
3. Počet atomů v mědi se rovná součinu Avogadrovy konstanty a látkového množství.
4. Hmotnost mědi vyjádříme pomocí součinu molární hmotnosti a látkového množství.
Hustota volných elektronů v kusu mědi je tedy přímo úměrná hustotě mědi a nepřímo úměrná molární hmotnosti mědi.
a) Řešení
Hustotu volných elektronů σ v kusu mědi vypočítáme ze vzorce:
\[ \sigma\,=\,\frac{N}{V}\,, \]kde N je počet volných elektronů a V je objem měděného kusu.
Nyní potřebujeme veličiny ve vzorci vyjádřit pomocí fyzikálních veličin, jejichž hodnotu známe nebo ji můžeme najít ve fyzikálních tabulkách. K tomu použijeme vztahy z molekulové fyziky.
Protože víme, že každý atom mědi přispívá jedním volným elektronem, je počet volných elektronů N roven počtu atomů v mědi. Platí tedy:
\[ N\,=\,nN_\mathrm{A}, \]kde n je látkové množství daného kusu mědi a NA Avogadrova konstanta.
Látkové množství n se rovná celkové hmotnosti mědi m vydělené její molární hmotností Mm:
\[ n\,=\,\frac{m}{M_\mathrm{m}}\,. \]Tyto vztahy dosadíme do vzorce pro výpočet hustoty volných elektronů:
\[ \sigma\,=\,\frac{N}{V}\,=\,\frac{nN_\mathrm{A}}{V}\,=\,\frac{mN_\mathrm{A}}{VM_\mathrm{m}}\,. \]Teď už si stačí jen uvědomit, že neznámá hmotnost mědi ve vzorci dělená objemem je hustota mědi ρ, kterou také najdeme v tabulkách.
Hustotu volných elektronů v kusu mědi tedy vypočítáme pomocí vztahu:
\[ \sigma\,=\,\frac{\rho N_\mathrm{A}}{M_\mathrm{m}}\,. \]a) Číselné dosazení
V minulém oddíle jsme zjistili, že hustotu volných elektronů ρ v kusu mědi vypočítáme ze vztahu:
\[ \sigma\,=\,\frac{\rho N_\mathrm{A}}{M_\mathrm{m}} \,, \]kde ρ je hustota mědi, NA Avogadrova konstanta a Mm molární hmotnost mědi.
Číselné hodnoty všech těchto veličin najdeme ve fyzikálních tabulkách:
\[ \rho\,=\,8{,}96\,\mathrm{g\,cm^{-3}}\,=\,8{,}96{\cdot}10^3\,\mathrm{kg\,m^{-3}} \] \[ N_\mathrm{A}\,=\,6{,}02{\cdot}10^{23}\,\mathrm{mol^{-1}} \] \[ M_\mathrm{m}\,=\,63{,}54\,\mathrm{g\,mol^{-1}}\,=\,63{,}54{\cdot}10^{-3}\,\mathrm{kg\,mol^{-1}}\,. \]Dosadíme-li veličiny v základních jednotkách, pak výsledná hustota volných elektronů v kusu mědi bude mít jednotku m-3:
\[ \sigma\,=\,\frac{\rho N_\mathrm{A}}{M_\mathrm{m}}\,=\,\frac{\,8{,}96{\cdot}10^3\,\cdot\,6{,}02\,\cdot\,10^{23}}{63{,}54{\cdot}10^{-3}}\,\mathrm{m^{-3}}\,\dot{=}\,8{,}5{\cdot}10^{28}\,\mathrm{m^{-3}}. \]b) Nápověda
Uvědomte si nebo vyhledejte, jaký je vztah mezi rychlostí pohybu elektronů a velikostí proudu, který protéká měděným drátem.
b) Rozbor
V případě pohybu volných elektronů ve vodiči platí, že celkový proud procházející vodičem se rovná součinu hustoty náboje, rychlosti uspořádaného pohybu elektronů a průřezu vodiče. Nábojovou hustotu získáme z hustoty elektronů, kterou jsme vypočítali již v oddíle a) Řešení, a velikosti elementárního náboje.
Vypočítaná rychlost je rychlost uspořádaného pohybu elektronů. Tedy tzv. driftová nebo unášivá rychlost.
b) Řešení
V případě pohybu volných elektronů ve vodiči vypočítáme celkový proud procházející vodičem ze vztahu (viz Nápověda k části b):
\[ I\,=\,e\sigma vS, \]kde e je elementární náboj jednoho elektronu, σ hustota elektronů a v rychlost uspořádaného pohybu elektronů v měděném drátu.
Vyjádříme si rychlost uspořádaného pohybu elektronů, tedy driftovou rychlost elektronů:
\[ v\,=\,\frac{I}{e\sigma S}. \]V oddíle a) Řešení jsme odvodili vztah pro výpočet hustoty elektronů:
\[ \sigma\,=\,\frac{\rho N_\mathrm{A}}{M_\mathrm{m}}, \]kde ρ značí hustotu mědi, NA je Avogadrova konstanta a Mm molární hmotnost mědi.
Pro průřez S měděného drátu o průměru d platí:
\[ S\,=\,\frac{\pi d^2}{4}. \]Oba tyto vztahy nyní dosadíme do vzorce pro výpočet rychlosti pohybu elektronů v:
\[ v\,=\,\frac{I}{e\sigma S}\,=\,\frac{I}{e\,\frac{\rho N_\mathrm{A}}{M_\mathrm{m}}\,\frac{\pi d^2}{4}} \]a vztah upravíme:
\[ v\,=\,\frac{4IM_\mathrm{m}}{e\rho\pi N_\mathrm{A} d^2}. \]Pozn.: Rychlost v je rychlost uspořádaného pohybu elektronů, tzv. driftová rychlost. Nejedná se o rychlost elektronů.
b) Číselné dosazení
V minulém oddíle jsme získali vztah pro výpočet rychlosti uspořádaného pohybu elektronů v (tzv. driftová nebo unášivá rychlost) v měděném drátu:
\[ v\,=\,\frac{4IM_\mathrm{m}}{e\rho\pi N_\mathrm{A} d^2}\,, \]kde I je proud procházející drátem, Mm molární hmotnost mědi, e je elementární náboj, ρ hustota mědi, NA Avogadrova konstanta a d průměr drátu.
V oddíle Zápis nalezneme číselné hodnoty všech těchto veličin:
I = 1 A d = 1 mm = 10-3 m Mm = 63,54 g mol-1 = 63,54·10-3 kg mol-1 e = 1,60 ·10-19 C ρ = 8,96 g cm-3 = 8,96·103 kg m-3 NA = 6,02 ·1023 mol-1 Po dosazení veličin v základních jednotkách bude výsledná rychlost uspořádaného pohybu elektronů v jednotkách m s-1:
\[ v\,=\,\frac{4IM_\mathrm{m}}{e\rho\pi N_\mathrm{A} d^2}\,=\,\frac{4{\cdot} 1\cdot 63{,}54}{1{,}60{\cdot} 10^{-19}\cdot 8{,}96{\cdot} 10^3\cdot \pi\cdot 6{,}02{\cdot} 10^{23}\cdot 10^{-6}}\,\mathrm{m\,s^{-1}}\] \[ v\,\dot{=}\,9{,}4{\cdot} 10^{-5}\,\mathrm{m\,s^{-1}}\,\dot{=}\,10^{-4}\,\mathrm{m\,s^{-1}}\,\dot{=}\,0{,}1\,\mathrm{mm\,s^{-1}}. \]b) Jak to je s okamžitým rozsvícením žárovky?
Rychlost uspořádaného pohybu elektronů ve vodiči je skutečně „hlemýždí“. Ale ze zkušenosti víme, že stiskneme-li elektrický spínač, žárovka se rozsvítí prakticky okamžitě a nemusíme čekat, až elektron „doputuje z jednoho konce drátu na druhý“. To je dáno tím, že rychlost, s jakou se žárovka rozsvítí, odpovídá rychlosti šíření elektrického signálu, a ne rychlosti elektronů.
Představme si to takto:
Stisknutím spínače spojíme elektrický obvod, a tím „šťouchneme“ do elektronu a ten se trochu posune. Tím se ale změní elektrické pole v jeho okolí a toto pole o kus dál postrčí jiný elektron. Ten opět změní elektrické pole ve svém okolí a to posune další elektron. Nakonec elektrické pole „šťouchne“ do posledního elektronu a rozsvítí se žárovka.
Rychlost šíření tohoto elektrického (resp. elektromagnetického) „šťouchnutí“ odpovídá rychlosti šíření světla v daném prostředí, neboť se vlastně jedná o pohyb elektromagnetické vlny.
c) Nápověda
Zkuste vyřešit nebo prostudujte úlohu Vzájemné silové působení dvou vodičů s proudem. V této úloze je podrobně vysvětleno, jakými magnetickými silami na sebe vzájemně působí dva dlouhé rovnoběžné vodiče.
c) Rozbor
Směr síly působící na dva rovnoběžné vodiče závisí na směru protékajícího proudu.
Jestliže oběma vodiči prochází proud stejným směrem, pak v oblasti mezi vodiči jdou indukční čáry obou magnetických polí proti sobě a pole se zeslabují. V oblasti vně vodičů mají indukční čáry obou polí stejný směr – pole se zesilují a vodiče jsou tlačeny k sobě.
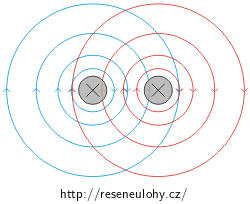
Pokud proud prochází opačnými směry, pak v oblasti mezi vodiči mají indukční čáry obou polí stejný směr – pole se zesilují. V oblasti vně vodičů jdou indukční čáry magnetických polí proti sobě, pole se zeslabují a vodiče jsou taženy od sebe.
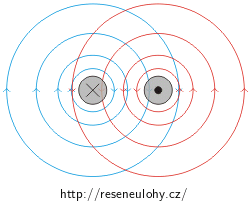
Na obrázku níže jsou znázorněny dva rovnoběžné, stejně dlouhé vodiče, které jsou označené 1 a 2. Oběma vodiči protéká proud stejným směrem. Pro přehlednost je do obrázku zakresleno magnetické pole jen prvního vodiče.
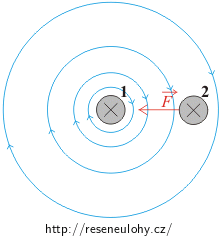
První vodič kolem sebe vytváří magnetické pole. Velikost indukce tohoto pole v místě druhého vodiče je přímo úměrná proudu procházejícímu prvním vodičem a nepřímo úměrná vzdálenosti obou vodičů.
Síla, která působí na druhý vodič, je pak přímo úměrná magnetické indukci prvního vodiče, proudu procházejícímu druhým vodičem a délce vodičů.
Pozn.: Stejně bychom mohli říct, že kolem druhého vodiče vzniká magnetické pole, jež ovlivňuje sílu působící na první vodič. Výsledné síly působící mezi vodiči mají však stejnou velikost (to plyne např. i z 3. Newtonova zákona).
c) Řešení a číselné dosazení
Mějme dva stejně dlouhé vodiče. Oběma vodiči teče proud stejným směrem, tyto vodiče se tedy navzájem přitahují. Velikost proudu I1, který protéká jedním vodičem, je shodná s proudem I2 protékajícím druhým vodičem. Tuto společnou hodnotu označíme I. Tedy:
\[ I_1\,=\,I_2\,=\,I. \]Pro přitažlivou magnetickou sílu Fm působící mezi vodiči platí:
\[ F_\mathrm{m}\,=\,\frac{\mu_0 I_1I_2l}{2\pi x}, \]kde µ0 je permeabilita prostředí, ve kterém jsou vodiče umístěny (tedy permeabilita vzduchu), l je délka vodičů a x vzdálenost mezi vodiči.
Na začátku tohoto oddílu jsme si řekli, že oběma vodiči protéká stejný proud I. Proto tedy:
\[ F_\mathrm{m}\,=\,\frac{\mu_0 I^2l}{2\pi x}\,. \]Číselné hodnoty veličin najdeme v oddíle Zápis:
µ0 = 4π·10-7 H m-1
I = 1 A
x = 1 cm = 10-2 m
Nyní se podívejme, jaká magnetická síla působí na jeden metr délky vodiče, tedy pro l = 1 m:
\[ F_\mathrm{m}\,=\,\frac{\mu_0 I^2l}{2\pi x}\,=\,\frac{4\pi\cdot 10^{-7}\cdot1^2{\cdot}1}{2\pi\cdot10^{-2}}\,\mathrm{N}\,=\,2{\cdot}10^{-5}\,\mathrm{N}. \]d) Nápovědy
d) Rozbor
Po odebrání kladných iontů z mřížky mědi budou mít oba „dráty“ konstantní délkovou hustotu náboje, která je přímo úměrná proudu procházejícímu dráty a nepřímo úměrná rychlosti volných elektronů.
Elektrické pole nekonečného rovnoměrně nabitého drátu míří v každém bodě kolmo na drát a směřuje k němu (je záporně nabitý). V dané vzdálenosti od sebe budí elektrickou intenzitu, jejíž velikost je přímo úměrná hustotě náboje a nepřímo úměrná vzdálenosti od drátu.
Elektrická odpudivá síla na jednotku délky pak bude rovna součinu délkové hustoty náboje a elektrické intenzity.
d) Řešení
Jestliže odebereme kladné ionty z mřížky mědi, pak oba vodiče budou mít konstantní délkovou hustotu náboje λ, pro kterou platí:
\[ \lambda\,=\,\frac{Q}{l}\hspace{10px}\Rightarrow\hspace{10px}Q\,=\,\lambda l, \]kde Q je náboj vodiče a l jeho délka.
Celkový proud I, který vodičem prochází, odpovídá podílu náboje Q a času t, po který proud vodičem prochází. Tedy:
\[ I\,=\,\frac{Q}{t}\hspace{10px}\Rightarrow\hspace{10px}Q\,=\,It \]a po dosazení dostáváme:
\[ \lambda\,=\,\frac{It}{l}\,. \]Délka vodiče l dělená časem t, za který proud vodičem projde, se rovná rychlosti uspořádaného pohybu elektronů v. Tedy:
\[ \lambda\,=\,\frac{I}{v}\,. \tag{*}\]Elektrické pole takového vodiče je radiální a ve vzdálenosti x od sebe budí intenzitu pole o velikosti:
\[ E\,=\,\frac{1}{2\pi\epsilon_0}\,\frac{\lambda}{x}, \]kde ε0 je permitivita vakua a x vzdálenost obou vodičů.
Protože jsou oba vodiče nabity záporně (odebrali jsme všechny kladné ionty), pak elektrická síla Fe, která na ně působí, je odpudivá. Pro tuto sílu platí:
\[ F_\mathrm{e}\,=\,QE. \]Do tohoto vzorce doplníme vztah pro intenzitu elektrického pole:
\[ F_\mathrm{e}\,=\,Q\,\frac{1}{2\pi\epsilon_0}\,\frac{\lambda}{x}\,. \]Nyní postupně dosadíme za celkový náboj Q = λl:
\[ F_\mathrm{e}\,=\,\lambda l\,\frac{1}{2\pi\epsilon_0}\,\frac{\lambda}{x}\,=\,\frac{1}{2\pi\epsilon_0}\,\frac{\lambda^2l}{x}\, \]a odvozený vztah (*) za hustotu náboje \(\lambda\,=\,\frac{I}{v}\):
\[ F_\mathrm{e}\,=\,\frac{1}{2\pi\epsilon_0}\,\frac{I^2l}{xv^2} \,=\,\frac{I^2l}{2\pi\epsilon_0xv^2}\,. \]d) Číselné dosazení
Z oddílu d) Řešení vezmeme vzorec pro výpočet přitažlivé elektrické síly Fe:
\[ F_\mathrm{e}\,=\,\frac{I^2l}{2\pi\epsilon_0xv^2}\,, \]I značí proud procházející drátem, l je délka drátů, ε0 permitivita vakua, x vzdálenost mezi dráty a v je průměrná rychlost elektronů v měděném drátu.
Číselné hodnoty těchto veličin jsou:
I = 1 A
ε0 = 8,85·10-12 F m-1
x = 1 cm = 10-2 m
v = 9,4·10-3 cm s-1 = 9,4·10-5 m s-1
Elektrická přitažlivá síla působící na jednotku délky vodiče (tedy l = 1 m):
\[ F_\mathrm{e}\,=\,\frac{I^2l}{2\pi\epsilon_0xv^2}\,=\,\frac{1^2{\cdot}1}{2\pi\cdot8{,}85{\cdot}10^{-12}\cdot10^{-2}\cdot9{,}4^2{\cdot}10^{-10}}\,\mathrm{N}\,=\,2{\cdot}10^{20}\,\mathrm{N}. \]d) Porovnání magnetické a elektrické síly
V minulém oddíle jsme zjistili, že pro elektrickou odpudivou sílu platí:
\[ F_\mathrm{e}\,=\,\frac{I^2l}{2\pi\epsilon_0xv^2}\,. \]V části c) této úlohy jsme získali vzorec pro velikost magnetické síly:
\[ F_\mathrm{m}\,=\,\frac{\mu_0 I^2l}{2\pi x}\,. \]Spočítejme podíl velikostí obou sil:
\[ \frac{F_\mathrm{e}}{F_\mathrm{m}}\,=\,\frac{\frac{I^2l}{2\pi\epsilon_0xv^2}}{\frac{\mu I^2l}{2\pi x}}\,=\,\frac{1}{\epsilon_0\mu_0v^2}\,. \]Z elektrické permitivity a magnetické permeability lze určit rychlost světla ve vakuu c. Platí:
\[ c\,=\,\frac{1}{\sqrt{\epsilon_0\mu_0}}\,. \]A tedy:
\[ c^2\,=\,\frac{1}{\epsilon_0\mu_0}\,. \]Tento vztah dosadíme do vzorce pro porovnání velikostí elektrické a magnetické síly působící mezi vodiči:
\[ \frac{F_\mathrm{e}}{F_\mathrm{m}}\,=\,\frac{1}{\epsilon_0\mu_0v^2}\,=\,\frac{c^2}{v^2}\,. \]Dosazením rychlosti v = 10-4 m s-1 (viz část b) této úlohy) zjistíme, že elektrická síla je 1025krát větší než síla magnetická.
Odpověď
Hustota volných elektronů v kusu mědi je 8,5·1028 m-3.
Průměrná rychlost uspořádaného pohybu elektronů v měděném drátu je přibližně 9,4·10-3 cm s-1.
Přitažlivá síla mezi dvěma měděnými dráty, které jsou od sebe vzdáleny 1 cm, má velikost 2·10-5 N na jednotku délky.
Odpudivá elektrická síla by byla přibližně 1025krát větší než přitažlivá magnetická síla. Její velikost tedy činí asi 2·1020 N na jednotku délky.




