Sbírka řešených úloh

Změna proudu potenciometrem

Úloha číslo: 184

Přestože se o potenciometru uvažuje zejména v souvislosti s regulací napětí na spotřebiči, vidíme, že jím zároveň měníme i proud procházející tímto spotřebičem.

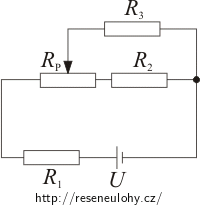
V jakém intervalu můžeme regulovat proud tekoucí rezistorem R₃ v zapojení podle obrázku? Jaké je napětí na rezistoru R₃ v krajních bodech tohoto intervalu? Jezdec potenciometru můžeme nastavit do libovolné polohy.

U = 30 V, R₁ = 100 Ω, R₂ = 20 Ω, R₃ = 1200 Ω, R_p = 105 Ω.

• Nápověda

  K určení intervalu nám stačí zjistit hodnoty jeho krajních bodů.

  Spočítejme tedy hodnoty proudu v případech, kdy jezdec bude v levé a pravé poloze potenciometru.

• Rozbor

  Abychom zjistili, v jakém intervalu lze regulovat proud procházející rezistorem R₃, určíme si hodnoty proudu v krajních bodech tohoto intervalu. Jezdec potenciometru posuneme do jeho krajních poloh A a B.

  

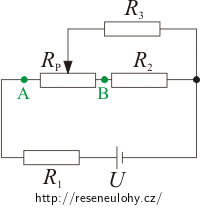
  Proud procházející rezistorem R₃ a napětí na tomto rezistoru budeme tedy počítat pro dvě různá zapojení.

  Při výpočtu využijeme vlastností sériového a paralelního zapojení rezistorů.

• Řešení – Jezdec v poloze A

  Jezdec potenciometru posuneme do polohy A a obvod si překreslíme tak, aby se nám s ním dobře pracovalo:

  

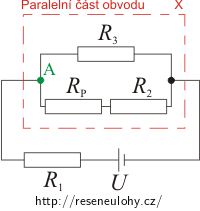
  Abychom mohli určit proud I_3A procházející rezistorem R₃, vypočítáme si nejprve celkový odpor paralelní části obvodu R_x:

  \[\frac{1}{R_\mathrm{x}}\,=\,\frac{1}{R_3}\,+\frac{1}{R_\mathrm{P}+R_2}\,=\,\frac{R_\mathrm{P}+R_2+R_3}{R_3\left(R_\mathrm{P}+R_2\right)}\] \[R_\mathrm{x}\,=\,\frac{R_3\left(R_\mathrm{P}+R_2\right)}{R_\mathrm{P}+R_2+R_3}\,.\tag{1}\]

  Celkové napětí při sériovém zapojení se rovná součtu napětí na jednotlivých prvcích. Pro celkové napětí tedy platí:

  \[U\,=\,U_1\,+\,U_\mathrm{x}\,,\]

  kde U₁ je napětí na rezistoru R₁ a U_x je napětí paralelní části obvodu.

  Velikost proudu, který protéká sériově zapojenými spotřebiči, je stejná:

  \[I_1\,=\,I_\mathrm{x}\hspace{10px}\Rightarrow\hspace{10px}\frac{U_1}{R_1}\,=\,\frac{U_\mathrm{x}}{R_\mathrm{x}}\,.\]

  A tedy:

  \[R_1U_\mathrm{x}\,=\,R_\mathrm{x}U_1\,.\]

  Z rovnice pro celkové napětí si vyjádříme napětí U₁ = U − U_x a dosadíme:

  \[R_1U_\mathrm{x}\,=\,R_\mathrm{x}\left(U\,-\,U_\mathrm{x}\right)\,.\]

  Nyní si vyjádříme napětí U_x:

  \[R_1U_\mathrm{x}\,+\,R_\mathrm{x}U_\mathrm{x}\,=\,R_\mathrm{x}U\] \[U_\mathrm{x}\left(R_1+R_\mathrm{x}\right)\,=\,R_\mathrm{x}U\] \[U_\mathrm{x}\,=\,\frac{R_\mathrm{x}U}{R_1+R_\mathrm{x}}\,.\]

  Napětí U_x je napětí na paralelní části obvodu a tedy i napětí na rezistoru R₃ (při paralelním zapojení je napětí na všech větvích stejné). Proto platí:

  \[I_\mathrm{3A}\,=\,\frac{U_\mathrm{x}}{R_3}\,.\]

  Dosazením za U_x získáme vztah pro výpočet hledaného proudu I_3A:

  \[I_\mathrm{3A}\,=\,\frac{R_\mathrm{x}U}{R_3\left(R_1+R_\mathrm{x}\right)}\,.\]

  Nyní ještě dosadíme vzorec (1) pro výpočet odporu paralelní části obvodu R_x:

  \[I_\mathrm{3A}\,=\,\frac{\frac{R_3\left(R_\mathrm{P}+R_2\right)}{R_\mathrm{P}+R_2+R_3}\,U}{R_3\left(R_1+\frac{R_3\left(R_\mathrm{P}+R_2\right)}{R_\mathrm{P}+R_2+R_3}\right)}\,.\]

  Po převedení na společného jmenovatele a úpravě složeného zlomku získáme konečný vztah pro výpočet proudu I_3A:

  \[I_\mathrm{3A}\,=\,\frac{\left(R_\mathrm{P}+R_2\right)\,U}{R_1R_3+\left(R_1+R_3\right)\left(R_\mathrm{P}+R_2\right)}\,.\]

• Řešení – Jezdec v poloze B

  Jezdec potenciometru posuneme do polohy B a obvod si překreslíme:

  

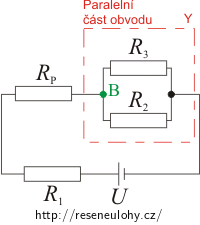
  Protože napětí ve větvích paralelní části obvodu je stejné (U_y = U₃), pro proud I₃ procházející rezistorem R_3B platí:

  \[I_\mathrm{3B}\,=\,\frac{U_\mathrm{y}}{R_3}\,,\tag{2}\]

  kde U_y je napětí na paralelní části obvodu.

  Celkové napětí v obvodu se sériově řazenými prvky se rovná součtu napětí na jednotlivých prvcích. Tedy:

  \[U\,=\,U_1\,+\,U_\mathrm{P}\,+\,U_\mathrm{y}\hspace{10px}\Rightarrow\hspace{10px}U_\mathrm{y}\,=\,U\,-\,U_1\,-\,U_\mathrm{P}\,.\]

  Při sériovém zapojení je celkový proud stejný jako proudy procházející jednotlivými prvky:

  \[I\,=\,I_1\,=\,I_\mathrm{P}\,.\]

  Podle Ohmova zákona se proud procházející spotřebičem rovná podílu napětí na spotřebiči a jeho odporu:

  \[I\,=\,I_1\,=\,\frac{U_1}{R_1}\hspace{50px}I\,=\,I_\mathrm{P}\,=\,\frac{U_\mathrm{P}}{R_\mathrm{P}}\,.\]

  Vzorec pro napětí v paralelní části obvodu si tedy můžeme přepsat:

  \[U_\mathrm{y}\,=\,U\,-\,R_1I\,-\,R_\mathrm{P}I\] \[U_\mathrm{y}\,=\,U\,-\,\left(R_1\,+\,R_\mathrm{P}\right)I\,.\tag{3}\]

  Z Ohmova zákona víme, že celkový proud I procházející obvodem se rovná podílu celkového napětí U a celkového odporu obvodu R:

  \[I\,=\,\frac{U}{R}\,.\]

  Abychom mohli určit celkový proud I, vypočítáme si nejprve celkový odpor soustavy R.

  Pro paralelní část obvodu platí:

  \[\frac{1}{R_\mathrm{y}}\,=\,\frac{1}{R_2}\,+\,\frac{1}{R_3}\,=\,\frac{R_2+R_3}{R_2R_3}\] \[R_\mathrm{y}\,=\,\frac{R_2R_3}{R_2+R_3}\,.\]

  Celkový odpor R:

  \[R\,=\,R_1\,+\,R_\mathrm{P}\,+\,R_\mathrm{y}\,=\,R_1\,+\,R_\mathrm{P}\,+\,\frac{R_2R_3}{R_2+R_3}=\,\frac{\left(R_1+R_\mathrm{P}\right)\left(R_2+R_3\right)+R_2R_3}{R_2+R_3}\,.\]

  Dosadíme do vztahu pro celkový proud:

  \[I\,=\,\frac{U}{R}\,=\,\frac{U}{\frac{\left(R_1+R_\mathrm{P}\right)\left(R_2+R_3\right)+R_2R_3}{R_2+R_3}}\,.\]

  A upravíme:

  \[I\,=\,\frac{U\left(R_2+R_3\right)}{\left(R_1+R_\mathrm{P}\right)\left(R_2+R_3\right)+R_2R_3}\,.\]

  Tento výsledek dosadíme do vzorce (3) pro napětí v paralelní části obvodu:

  \[U_\mathrm{y}\,=\,U\,-\,\left(R_1\,+\,R_\mathrm{P}\right)\frac{U\left(R_2+R_3\right)}{\left(R_1+R_\mathrm{P}\right)\left(R_2+R_3\right)+R_2R_3}\,.\]

  Po převedení pravé strany vzorce na společného jmenovatele získáme:

  \[U_\mathrm{y}\,=\,\frac{R_2R_3U}{\left(R_1+R_\mathrm{P}\right)\left(R_2+R_3\right)+R_2R_3}\,.\]

  Tento vztah dosadíme do vzorce (2) a získáme tak hledaný proud I_3B:

  \[I_\mathrm{3B}\,=\,\frac{U_\mathrm{y}}{R_3}\,=\,\frac{\frac{R_2R_3U}{\left(R_1+R_\mathrm{P}\right)\left(R_2+R_3\right)+R_2R_3}}{R_3}\,=\,\frac{R_2U}{\left(R_1+R_\mathrm{P}\right)\left(R_2+R_3\right)+R_2R_3}\,.\]

• Řešení – Jezdec v poloze B (jednodušeji)

  Porovnáme zapojení obvodu s jezdcem potenciometru v poloze B se zapojením, kdy je jezdec v poloze A:

  

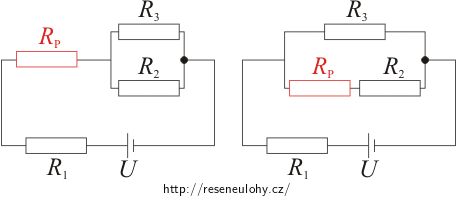
  Z obrázku je patrné, že:

  a) Místo sériově zapojeného potenciometru R_P a rezistoru R₂ máme nyní v paralelní větvi jen rezistor R₂. Celkový odpor této větve je tedy R₂.

  b) Potenciometr R_P se přesunul za rezistor R₁. Je s ním tedy spojen sériově a celkový odpor této sériové části obvodu je R₁ + R_P.

  Vzorec pro výpočet proudu I_3B procházejícího rezistorem R₃ při posunutí jezdce potenciometru do polohy B získáme úpravou konečného výsledku oddílu Řešení 1.

  \[I_\mathrm{3A}\,=\,\frac{\left(R_P+R_2\right)\,U}{R_1R_3+\left(R_1+R_3\right)\left(R_\mathrm{P}+R_2\right)}\]

  Místo R_P + R₂ dosadíme do vzorce jen R₂ (viz a)) a R₁ nahradíme vztahem R₁ + R_P (viz b)). Tedy:

  \[I_\mathrm{3B}\,=\,\frac{R_2\,U}{\left(R_1+R_\mathrm{P}\right)R_3+\left[\left(R_1+R_\mathrm{P}\right)+R_3\right]R_2}\,.\]

  Jmenovatel zlomku ještě upravíme (vytkneme výraz (R₁ + R_P)) a získáme stejný výsledek jako v předchozí části:

  \[I_\mathrm{3B}\,=\,\frac{R_2\,U}{\left(R_1+R_\mathrm{P}\right)\left(R_2+R_3\right)+R_2R_3}\,.\]

• Číselné dosazení

  Do výsledných vzorců, které jsme získali řešením úlohy

  \[I_\mathrm{3A}\,=\,\frac{\left(R_\mathrm{P}+R_2\right)\,U}{R_1R_3+\left(R_1+R_3\right)\left(R_\mathrm{P}+R_2\right)}\] \[U_\mathrm{3A}\,=\,I_\mathrm{3A}R_3\] \[I_\mathrm{3B}\,=\,\frac{R_2U}{\left(R_1+R_\mathrm{P}\right)\left(R_2+R_3\right)+R_2R_3}\] \[U_\mathrm{3B}\,=\,I_\mathrm{3B}R_3,\]

  dosadíme hodnoty ze zadání úlohy:

  U = 30 V, R₁ = 100 Ω, R₂ = 20 Ω, R₃ = 1200 Ω, R_p = 105 Ω:

  \[I_\mathrm{3A}\,=\,\frac{125{\cdot} 30}{120000+1300{\cdot} 125}\,\mathrm{A}\,=\,13{,}3{\cdot} 10^{-3}\,\mathrm{A}\,=\,13{,}3\,\mathrm{mA}\] \[U_\mathrm{3A}\,=\,13{,}3{\cdot} 10^{-3}\cdot 1200\,\mathrm{V}\,=\,16\,\mathrm{V}\] \[I_\mathrm{3B}\,=\,\frac{20{\cdot} 30}{205{\cdot} 1220+20{\cdot} 1200}\,\mathrm{A}\,=\,2{,}2{\cdot} 10^{-3}\,\mathrm{A}\,=\,2{,}2\,\mathrm{mA}\] \[U_\mathrm{3B}\,=\,2{,}2{\cdot} 10^{-3}\cdot 1200\,\mathrm{V}\,=\,2{,}6\,\mathrm{V}\,.\]

• Odpověď

  Proud tekoucí rezistorem R₃ můžeme regulovat v intervalu od 2,2 mA do 13,3 mA. Hodnoty napětí na rezistoru R₃ v krajních bodech intervalu jsou 16 V a 2,6 V, přičemž vyšší hodnota napětí odpovídá nižší hodnotě proudu.

• Hodnota proudu v obecné poloze jezdce

  Řekli jsme, že proud I₃ bude dosahovat minimální a maximální hodnoty v krajních polohách jezdce potenciometru. Nyní by bylo vhodné si ověřit, že toto naše tvrzení je pravdivé.

  Překreslíme si obvod tak, abychom znázornili, že je jezdec potenciometru v obecné poloze:

  

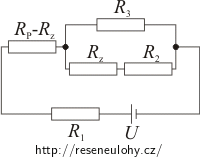
  Součet odporů rezistorů R_P − R_z a R_z se rovná odporu potenciometru R_P. Odpor rezistoru R_z může nabývat hodnot od 0 Ω do 105 Ω (odpor potenciometru R_P).

  Stejným způsobem jako ve třetí části řešení si vzorec pro proud I_3A

  \[ I_\mathrm{3A}\,=\,\frac{\left(R_\mathrm{P}+R_2\right)\,U}{R_1R_3+\left(R_1+R_3\right)\left(R_\mathrm{P}+R_2\right)} \]

  upravíme tak, aby vyhovoval poloze jezdce v obecné poloze. Výraz (R_P+R₂) nahradíme vztahem (R_z+R₂) a R₁ ve vzorci nahradíme výrazem (R_P−R_z)+R₁. Tedy:

  \[I_3\,=\,\frac{\left(R_\mathrm{z}+R_2\right)\,U}{\left[\left(R_\mathrm{P}-R_\mathrm{z}\right)+R_1\right]R_3+\left[\left(R_\mathrm{P}-R_\mathrm{z}\right)+R_1+R_3\right]\left(R_\mathrm{z}+R_2\right)}\,.\]

  Jmenovatel zlomku upravíme vytýkáním před závorku a získáme tak konečnou rovnici pro výpočet proudu I₃ pro jezdce potenciometru v obecné poloze:

  \[I_3\,=\,\frac{\left(R_\mathrm{z}+R_2\right)U}{\left(R_\mathrm{P}-R_\mathrm{z}+R_1\right)\left(R_3+R_\mathrm{z}+R_2\right)+R_3\left(R_\mathrm{z}+R_2\right)}\,.\]

  Nyní si vytýkáním před závorku a roznásobováním závorek upravíme zlomek tak, abychom si v čitateli i jmenovateli zvlášť vyjádřili členy s R_z a R_z²:

  \[ I_3\,=\,\frac{R_\mathrm{z}U+R_2U}{-R_\mathrm{z}^2+R_\mathrm{z}\left(R_\mathrm{P}+R_1-R_2\right)+\left[\left(R_\mathrm{P}+R_1\right)\left(R_3+R_2\right)+R_3R_2\right]}\,. \]

  Abychom zjistili minimální a maximální hodnotu proudu I₃, zderivujeme tento vzorec podle R_z. Pro derivaci podílu dvou funkcí f, g, kde g ≠ 0 platí:

  \[ \left(\frac{f}{g}\right)^,\,=\,\frac{f^,g-fg^,}{g^2}\,. \]

  Pozn.: přehled základních vzorců pro derivování najdete v úloze Paúhoř elektrický.

  Za předpokladu, že jmenovatel zlomku I₃ je nenulový, můžeme tento vzorec pro derivaci podílu použít. Platí:

  \[ f\,=\,U\left(R_\mathrm{z}\,+\,R_2\right) \] \[ g\,=\,-R_\mathrm{z}^2+R_\mathrm{z}\left(R_\mathrm{P}+R_1-R_2\right)+\left(R_\mathrm{P}+R_1\right)\left(R_3+R_2\right)+R_3R_2\,. \]

  A tedy:

  \[f^,\,=\,U\] \[g^,\,=\,-2R_\mathrm{z}\,+\,\left(R_\mathrm{P}\,+\,R_1\,-\,R_2\right)\,,\]

  kde \(f^,\), \(g^,\) jsou funkce \(f\), \(g\) zderivované podle \(R_z\).

  Protože funkce g je nenulová, pak pro její druhou mocninu platí:

  \[g^2\,>\,0\,.\]

  Nyní se podíváme, jak je to s velikostí funkce \(f^,g-fg^,\):

  \[f^,g=U\left(-R_\mathrm{z}^2+R_\mathrm{z}\left(R_\mathrm{P}+R_1-R_2\right)+\left(R_\mathrm{P}+R_1\right)\left(R_3+R_2\right)+R_3R_2\right)\] \[fg^,=U\left(R_\mathrm{z}\,+\,R_2\right)\left[-2R_\mathrm{z}\,+\,\left(R_\mathrm{P}\,+\,R_1\,-\,R_2\right)\right]\,.\]

  Pokud od sebe tyto dvě funkce odečteme, získáme výsledek:

  \[f^,g-fg^,\,=\,U\left(R_\mathrm{z}^2+2R_2R_\mathrm{z}+R_\mathrm{P}R_3+R_1R_3+R_2^2\right)\,.\]

  Díky tomu, že odpory R₁, R₂, R_P a napětí U nabývají kladných hodnot a odpor rezistoru R_z se pohybuje od 0 Ω do velikosti odporu R_P, pak pro funkci \(f^,g-fg^,\) platí:

  \[f^,g-fg^,\,>\,0\,.\]

  První derivace \(\frac{dI_3}{dR_\mathrm{z}}\) je tedy kladná, a proto funkce I₃ v závislosti na R_z je rostoucí.

  Náš přístup pro výpočet krajních hodnot proudu I₃ byl tedy správný. Minimální hodnoty proud I₃ nabývá pro R_z = 0 Ω. To odpovídá poloze jezdce potenciometru v bodě B. Maximální hodnotu má proud I₃, pokud R_z = R_P, tedy pro jezdec potenciometru v poloze A.

• Odkaz na úlohu

  Vyzkoušejte si také vyřešit úlohu Potenciometr.