Sbírka řešených úloh

Smyčka ve smyčce

Úloha číslo: 258

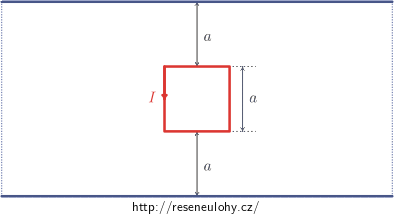
Čtvercová smyčka z drátu o straně a je umístěna uprostřed mezi dvěma dlouhými přímými vodiči, jejichž vzájemná vzdálenost je 3a. Dlouhé vodiče jsou spojeny dvěma vodiči (čárkovaně naznačenými na obrázku níže), které se nachází velmi daleko od čtvercové smyčky. Proud ve čtvercové smyčce konstantně roste v čase,

tj.  \(\frac{\mathrm dI}{\mathrm dt} = k\).

Jaké elektromotorické napětí se indukuje ve velké smyčce? Jakým směrem poteče indukovaný proud?

• Rozbor

  Pro přímý výpočet napětí indukovaného polem ve velké smyčce by bylo třeba spočítat přesně pole malé smyčky, což je možné, ale bylo by velmi obtížné jej integrovat při výpočtu magnetického indukčního toku. Pokusíme se tedy využít poznatků o vzájemné indukci. Magnetický indukční tok velkou smyčkou, který vyvolá proud I v malé smyčce, musí být stejně velký jako magnetický indukční tok malou smyčkou, který vyvolá proud I tekoucí ve velké smyčce.

  Magnetický indukční tok (jednou ze smyček) je totiž v obou případech přímo úměrný proudu (ve druhé smyčce) a konstanta přímé úměrnosti je konstantou vzájemné indukčnosti (tohoto uspořádání), která je v obou případech stejná.

  Poznámka: Podrobnější zdůvodnění tohoto faktu najdete v komentáři k úloze Krátký a dlouhý solenoid.

  Pole velké smyčky je ale snadnější na počítání, protože jde vlastně o superpozici polí dvou velmi dlouhých drátů. Příspěvky krátkých spojovacích vodičů ve velmi velké vzdálenosti můžeme totiž zanedbat.

• Nápověda 1

  Řešte duální úlohu: Uvažujte, že proud I teče velkou smyčkou, a zkuste spočítat indukční tok malou smyčkou.

  Uvažte, že vzhledem k velmi velké vzdálenosti spojujících vodičů velké smyčky od malé smyčky se uplatní pouze magnetické pole generované dlouhými přímými vodiči velké smyčky umístěnými ve vzdálenosti a po obou stranách malé smyčky.

• Nápověda 2

  Bude se příspěvek k indukčnímu toku od dlouhých vodičů velké smyčky lišit?

• Řešení nápovědy 2

  Vzhledem k symetrii situace a vzhledem k tomu, že proud jimi teče opačnými směry, nikoliv. Oba příspěvky budou stejně velké.

• Nápověda 3

  Příspěvek k indukčnímu toku skrze malou smyčku od dlouhého vodiče spočtěte takto:

  Magnetické pole dlouhého vodiče s proudem závisí pouze na velikosti proudu a na vzdálenosti od něj.

  Malou smyčku proto „rozřežte“ vodorovně (tj. rovnoběžně se směrem dlouhého vodiče) na obdélníčky o obsahu dS malé tloušťky dr s vodorovnou stranou délky a.

  

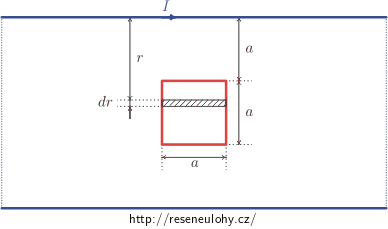
  V tomto obdélníčku je magnetické pole přibližně homogenní a má velikost

  \[B = \frac{\mu_0I}{2\pi r},\]

  kde r je kolmá vzdálenost obdélníčku od dlouhého drátu. Tok obdélníčkem je tedy

  \[{\rm d}\Phi = B\,{\rm d}S = \frac{\mu_0I}{2\pi r}\,(a\,{\rm d}r).\]

  Celkový indukční tok určete integrací přes všechny tyto obdélníčky.

  Poznámka: Můžete se též zkusit inspirovat podobnou úlohu Magnetický tok čtvercem.

• Řešení

  Je obtížné spočítat přesně tok velkou smyčkou v případě, kdy teče proud malou smyčkou, proto budeme řešit duální úlohu. Stejný proud necháme procházet velkou smyčkou a spočítáme indukční tok smyčkou malou.

  Výsledek duální úlohy je formálně stejný jako výsledek úlohy původní, neboť pro indukční tok platí vztah Φ = MI, tj. indukční tok je v obou případech přímo úměrný proudu skrze stejnou konstantu M — konstantu vzájemné indukčnosti (obou smyček).

  

  Příspěvek od spojovacích vodičů, které jsou velmi daleko, můžeme zanedbat. Příspěvky Φ₁ od obou dlouhých drátů jsou vzhledem k symetrii situace stejné, takže

  \[\Phi = 2\Phi_1 = 2\int_\mathrm{S} \vec B \cdot \mathrm{d}\vec S.\]

  Z nápovědy víme, že je vhodné integrovat přes úzké vodorovné obdélníčky s plochou dS = adr, kde r je vzdálenost obdélníčku od vodiče. Integrovat budeme v mezích od a do 2a. Pro velikost magnetické indukce B v místě obdélníčku platí

  \[B = \frac{\mu_0I}{2\pi r}.\]

  Integrací tedy dostáváme

  \[\Phi = 2 \int_\mathrm{a}^\mathrm{2a} \frac{\mu_0I}{2\pi r}\,a\,\mathrm{d}r = 2a\frac{\mu_0I}{2\pi}\,\ln\frac{2a}{a} = \frac{\mu_0aI}{\pi}\,\ln 2.\]

  Odtud plyne, že velikost indukovaného napětí je

  \[|U_\mathrm{e}| = \frac{\mathrm{d}\Phi}{\mathrm{d}t} = \frac{\mu_0a\,\ln 2}{\pi}\,\frac{\mathrm{d}I}{\mathrm{d}t} = \frac{\mu_0ka\,\ln 2}{\pi}.\]

  Jak už jsme zmínili dříve, je spočítaná hodnota elektromotorického napětí stejná i pro původní děj, kdy proud teče krátkou smyčkou a napětí se indukuje mezi konci dlouhých drátů.

  Směr indukovaného proudu ve velké smyčce musí mít takový směr, aby tlumil sílící magnetické pole malé smyčky (podle Lenzova zákona). Směr obíhání proudu ve velké smyčce bude tedy mít opačný smysl než v malé čtvercové smyčce.

• Odpověď

  Velikost indukovaného napětí ve velké smyčce je

  \[|U_\mathrm{e}| = \frac{\mu_0ka\,\ln 2}{\pi}.\]

  Indukovaný proud ve velké smyčce musí mít takový směr, aby tlumil sílící magnetické pole malé smyčky (podle Lenzova zákona). Směr obíhání proudu ve velké smyčce bude tedy mít opačný smysl než v malé čtvercové smyčce.

• Podobná úloha

  Krátký a dlouhý solenoid