Sbírka řešených úloh

Kulička na vlákně

Úloha číslo: 714

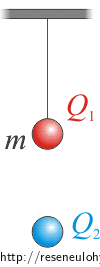
Tenké vlákno vydrží maximální sílu napnutí 10 mN. Na tomto vlákně je zavěšena kulička o hmotnosti 0,6 g s kladným nábojem 11 nC. Zdola k ní ve směru závěsu přibližujeme kuličku se záporným nábojem 13 nC.

Při jaké vzdálenosti mezi oběma kuličkami se vlákno přetrhne?

• Nápověda

  Nakreslete si obrázek sil působících na nabitou kuličku.

  Co musí platit pro velikost výslednice těchto sil?

• Rozbor

  Na zavěšenou kuličku působí tíhová a elektrická síla. Obě tyto síly namáhají vlákno, na kterém je kulička zavěšena. Velikost tíhové síly se nemění. Elektrická síla se při přibližování druhé kuličky v souladu s Coulombovým zákonem zvětšuje.

  Druhou kuličku můžeme přibližovat do té doby, dokud velikost výslednice tíhové a elektrické síly nepřekročí maximální sílu napnutí, kterou vlákno závěsu vydrží.

• Řešení

  

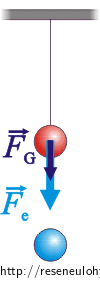
  Vlákno je namáháno tíhovou silou působící na kuličku a silou elektrickou, která se při přibližování druhé kuličky v souladu s Coulombovým zákonem zvětšuje.

  Velikost tíhové síly vypočítáme ze vzorce F = mg a velikost elektrické síly z Coulombova zákona \(F_\mathrm{e}\,=\,\frac{1}{4 \pi \varepsilon_0}\frac{Q_1 Q_2}{r^2}\).

  K přetržení vlákna dojde v okamžiku, kdy součet obou uvedených sil dosáhne maximální síly napnutí F_N.

  Platí tedy: \(F_\mathrm{N}\,=\,F_\mathrm{G}\,+\,F_\mathrm{e}\).

  Po dosazení ze vztahu pro tíhovou sílu a Coulombova zákona dostáváme:

  \[F_\mathrm{N}\,=\,mg\,+\,\frac{1}{4 \pi \varepsilon_0}\frac{Q_1 Q_2}{r^2}.\]

  Nyní již vyjádříme vzdálenost r, při níž dojde k přetržení vlákna:

  \[F_\mathrm{N}\,=\,mg\,+\,\frac{1}{4 \pi \varepsilon_0}\frac{Q_1 Q_2}{r^2} \hspace{40px}|\,-mg,\] \[F_\mathrm{N}\,-mg\,=\,\frac{1}{4 \pi \varepsilon_0}\frac{Q_1 Q_2}{r^2} \hspace{40px}|\,\cdot r^2,\] \[r^2 \left(F_\mathrm{N}\,-mg\right)\,=\,\frac{1}{4 \pi \varepsilon_0}\frac{Q_1 Q_2}{1} \hspace{40px}|\,: \left(F_\mathrm{N}\,-mg\right),\] \[r^2 \,=\,\frac{1}{4 \pi \varepsilon_0}\frac{Q_1 Q_2}{\left(F_\mathrm{N}\,-mg\right)},\] \[r\,=\,\sqrt{\frac{1}{4 \pi \varepsilon_0}\frac{Q_1 Q_2}{\left(F_\mathrm{N}\,-mg\right)}}.\]

• Zápis a číselný výpočet

  Q₁ = 11 nC = 11·10⁻⁹ C

  Q₂ = 13 nC = 13·10⁻⁹ C

  F_N = 10 mN = 10·10⁻³ N

  m = 0,6 g = 6·10⁻⁴ kg

  Z tabulek

  ε₀ = 8,85·10⁻¹² C²N⁻¹m⁻²

  g = 9,81 m s⁻²

  ---

  \[\begin{eqnarray} r\,&=&\,\sqrt{\frac{1}{4 \pi \varepsilon_0}\frac{Q_1 Q_2}{\left(F_\mathrm{N}\,-mg\right)}}\\ r\,&=&\,\sqrt{\frac{1}{4 \pi \cdot 8{,}85{\cdot} 10^{-12}}\,\frac{11{\cdot} 10^{-9}\cdot13{\cdot} 10^{-9}}{\left(10^{-2}\,-6{\cdot} 10^{-4}\cdot 9{,}81\right)}}\,\mathrm{m}\\ r\,&\dot=&\,0{,}018\,\mathrm{m}\,\dot=\,1{,}8\,\mathrm{cm} \end{eqnarray}\]

• Odpověď

  K přetržení vlákna dojde při vzdálenosti

  \[r\,=\,\sqrt{\frac{1}{4 \pi \varepsilon_0}\frac{Q_1 Q_2}{\left(F_\mathrm{N}\,-mg\right)}}\dot=\,1{,}8\,\mathrm{cm}\,.\]