Obvod s přepínačem

Úloha číslo: 78

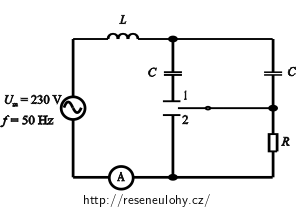
Generátor na obrázku dodává střídavé napětí 230 V o frekvenci 50 Hz. V obvodu je zapojena cívka, dva stejné kondenzátory a rezistor o neznámých hodnotách impedancí. Při rozpojení přepínačů (jako na obrázku) je napětí zpožděno za proudem generátoru o 20°. S přepínačem v poloze 1 napětí předbíhá proud generátoru o 10°. Když je přepínač v poloze 2, teče obvodem proud 2 A.

Určete odpor rezistoru, indukčnost cívky a kapacitu kondenzátoru.

Zápis

Ze zadání známe:

Napětí na zdroji:	U_m = 230 V
Frekvence napětí zdroje:	f = 50 Hz
Rozpojený přepínač:	napětí se za proudem zpožďuje o φ₁ = −20°
Přepínač v poloze jedna:	napětí předbíhá proud o φ₂ = 10°
Přepínač v poloze dva:	obvodem protéká proud I = 2 A

Chceme určit:

Odpor rezistoru:	R = ? (Ω)
Indukčnost cívky:	L = ? (H)
Kapacitu kondenzátoru:	C = ? (F)

Nápověda
Prohlédněte si schéma zapojení. Zaměřte se zejména na to, jak v jednotlivých polohách přepínače teče obvodem proud. Jednotlivé případy si překreslete tak, že vynecháte ty části obvodu, kterými proud neprotéká.
Rozbor
Ze zadání známe tři vlastnosti obvodu pro tři různé polohy přepínače. Máme také určit tři neznámé veličiny. To znamená, že každý zadaný údaj o obvodu převedeme na rovnici, a tím získáme soustavu rovnic, kde jako neznámé budou vystupovat odpor rezistoru, kapacita kondenzátoru a indukčnost cívky.

Původní obvod si rozkreslíme do jednotlivých zapojení podle polohy přepínače. U těchto obvodů zakreslíme pouze prvky, kterými poteče proud. Ty části obvodu, kterými proud neprotéká, vynecháme.

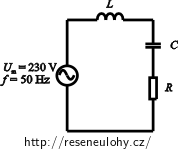
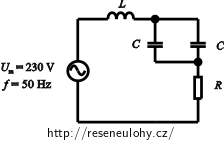
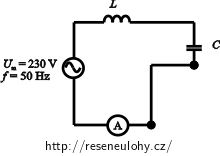
Pomocí Ohmova zákona vyjádříme fázové posuny mezi napětím a proudem pro rozpojený přepínač a přepínač v poloze 1. Dále si vyjádříme velikost impedance, která v zapojení s přepínačem v poloze 2 sestává jen z induktance a kapacitance.

Dostaneme opravdu tři rovnice (z každého obvodu jednu) pro tři neznámé hodnoty, tj. kapacitanci, induktanci a rezistanci. Soustavu vyřešíme a ze získaných hodnot vypočteme hodnotu kapacity, indukčnosti a odporu.
Řešení pomocí rozkreslených obvodů
Obvod s rozpojeným přepínačem:

Pro fázový posun v takovémto obvodu platí:
\[\mathrm{tg\,} {\varphi}_1 = \frac{X_\mathrm{L}-X_\mathrm{C}}{R}.\tag{1}\]
Fázový posun mezi napětím a proudem bude záporný, protože napětí je za proudem zpožďováno.

Obvod s přepínačem v poloze 1:

Celková kapacita v tomto zapojení je:

\[C_\mathrm{p}=C+C\] .

Celková kapacitance má potom tvar:

\[X_\mathrm{C_{p}}=\frac{1}{4\pi f C}=\frac{1}{2}X_\mathrm{C}.\]

Hodnota kapacitance v tomto zapojení je poloviční než v případě s rozpojeným přepínačem, protože jsou připojeny dva paralelní kondenzátory o stejné kapacitě.

Pro fázový posun v tomto obvodu platí:
\[\mathrm{tg\,} {\varphi}_2 =\frac{X_\mathrm{L}-\frac{1}{2}X_\mathrm{C}}{R}.\tag{2}\]
Fázový posun mezi napětím a proudem bude kladný, protože napětí předbíhá proud.

Obvod s přepínačem v poloze 2:

Proud přes rezistor nepoteče. Známe proud protékající ampérmetrem. V tomto obvodu můžeme tedy vypočítat velikost celkové impedance Z, která je složena z induktance a kapacitance:
\[Z=|X_\mathrm{L}-X_\mathrm{C}|=\frac{U_\mathrm{m}}{I}.\tag{3}\]
Řešení soustavy rovnic
Z rozkreslených obvodů jsme v předchozím oddíle získali soustavu tří rovnic o třech neznámých. Impedance budeme uvažovat v ohmech a pro přehlednost je nebudeme psát do rovnic.

Z obvodu s rozpojeným přepínačem:

\[ \frac{X_\mathrm{L}-X_\mathrm{C}}{R}=\mathrm{tg\,} {\varphi}_1 =\mathrm{tg\,} (-20^{\circ}) \,\dot{=}\,-0{,}364.\tag{1}\]

Z obvodu s polohou přepínače 1:
\[\frac{X_\mathrm{L}-\frac{1}{2}X_\mathrm{C}}{R}=\mathrm{tg\,} {\varphi}_2 =\mathrm{tg\,} (10^{\circ}) \,\dot{=}\,0{,}18.\tag{2}\]
Z obvodu s polohou přepínače 2:
\[|X_\mathrm{L}-X_\mathrm{C}|=\frac{U_\mathrm{m}}{I}=\frac{230}{2} = 115. \tag{3}\]
Do rovnice (1) dosadíme rovnici (3) a vyjádříme velikost rezistance. Zároveň můžeme „odstranit“ absolutní hodnotu u rozdílu |X_L - X_C|, protože rezistance R je kladná, platí:
\[X_\mathrm{L}-X_\mathrm{C}=-115.\]
Dosadíme do rovnice (1):
\[ \frac{X_\mathrm{L}-X_\mathrm{C}}{R}=\mathrm{tg\,} {\varphi}_2 \] \[\frac{-115}{R}\,\dot{=}\,-0{,}364\] \[R\,\dot{=}\, 316.\]
Nyní jsme úlohu upravili na řešení dvou rovnic o dvou neznámých. Jsou to upravené rovnice (1) a (2), do kterých jsme dosadili vypočtenou hodnotu rezistance R:

\[X_\mathrm{L}-X_\mathrm{C}=-115\tag{1}\]

\[X_\mathrm{L}-\frac{1}{2}X_\mathrm{C}=0{,}18R\,\dot{=}\,56{,}88.\tag{2}\]

Z první z nich vyjádříme:
\[X_\mathrm{L}=-115+X_\mathrm{C}\]
a dosadíme do druhé:
\[-115+X_\mathrm{C}-\frac{1}{2}X_\mathrm{C}\,\dot{=}\,56{,}88.\]
Dostaneme:
\[X_\mathrm{C}\,\dot{=}\,2(56{,}88+115)\,\dot{=}\,344\] \[X_\mathrm{L}\,\dot{=}\,-115+344\,\dot{=}\,229.\]

Hodnoty odporu rezistoru, kapacity kondenzátoru a indukčnosti cívky (s jednotkami):
- Odpor rezistoru: \[R\,\dot{=}\, 316\,\mathrm \Omega\]
- Kapacita kondenzátoru: \[X_\mathrm{C}=\frac{1}{2 \pi f C}\] \[C=\frac{1}{2 \pi f X_\mathrm{C}}\,\dot{=}\,\frac{1}{ 2 \pi \cdot 50 {\cdot} 344}\,\mathrm F\] \[C\,\dot{=}\,9{,}3 \,\mathrm{\mu F}\]
- Indukčnost cívky: \[X_\mathrm{L}= 2 \pi f L\] \[L=\frac{X_\mathrm{L}}{2 \pi f}\,\dot{=}\,\frac{229}{2 \pi \cdot 50}\,\mathrm H\] \[L\,\dot{=}\,0{,}73\,\mathrm H\]
Odpověď
Odpor rezistoru v obvodu je přibližně: R = 316 Ω.

Indukčnost cívky v obvodu má hodnotu asi: L = 0,73 H.

Kapacity kondenzátorů v obvodu mají hodnotu přibližně: C = 9,3 μF.