Sbírka řešených úloh

Pojistka v obvodu se stejnosměrným proudem

Úloha číslo: 721

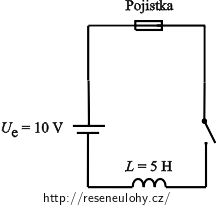
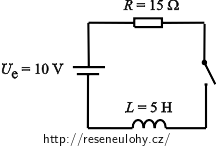
V obvodu se stejnosměrným napětím je zapojena ideální cívka o indukčnosti 5 H, rezistor s odporem 15 Ω, spínač a ideální pojistka. Hodnota elektromotorického napětí zdroje je 10 V.

Ideální pojistka má nulový odpor do chvíle, kdy proud jí protékající dosáhne hodnoty 3 A. Po dosažení této hodnoty se pojistka přepálí a její odpor bude nekonečný.

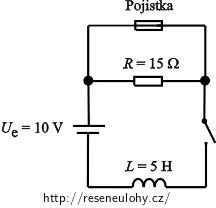
V čase t = 0 s sepneme spínač S.

a) Za jak dlouho se po sepnutí spínače pojistka přepálí?

b) Určete závislost proudu protékajícího cívkou na čase. Pro zjednodušení výpočtu po přepálení pojistky začněte měřit čas znovu od nuly.

• Nápověda 1

  V obvodu, ve kterém je zapojen pouze zdroj stejnosměrného napětí a cívka, roste proud neomezeně do té doby, než dojde ke zničení cívky, zdroje nebo k přepálení vodičů. Z těchto důvodů je v obvodu zapojena pojistka, která se při určité hodnotě proudu přepálí a zabrání zničení obvodu.

• Nápověda 2

  Uvědomte si, kudy teče v obvodu proud před a po přepálení pojistky.

• Řešení nápovědy

  Před přepálením pojistky protéká proud pouze pojistkou, nikoli rezistorem (díky nulovému odporu pojistky). Obvod můžeme překreslit takto:

  

  Po přepálení pojistky protéká proud rezistorem, viz obrázek:

  

• Rozbor

  Než se přepálí pojistka, roste proud v obvodu (jeho růst není ničím omezen). Napětí zdroje musí být podle Lenzova zákona v každém okamžiku stejné jako napětí indukované na cívce. Z tohoto poznatku lze odvodit závislost proudu na čase a poté vyjádřit čas, kdy dojde k přepálení pojistky.

  Dojde-li k přepálení pojistky, začne proud protékat větví s rezistorem. Platí, že součet napětí indukovaného na cívce a napětí zdroje je roven úbytku napětí na rezistoru. Pomocí této skutečnosti sestavíme rovnici pro průběh proudu v obvodu.

• a) Řešení – doba přepálení pojistky

  Do chvíle, než se přepálí pojistka, je odpor celého obvodu nulový (větví s rezistorem neprotéká žádný proud). Okamžitý proud i tekoucí obvodem postupně roste a v cívce se indukuje napětí U_L, které v souladu s Lenzovým zákonem působí proti tomuto růstu. Napětí zdroje U_e musí být podle 2. Kirchhoffova zákona v každém okamžiku stejné jako napětí indukované na cívce. Musí tedy platit

  \[ U_\mathrm{e} = U_\mathrm{L}. \]

  Dosadíme za indukované napětí na cívce z Lenzova zákona:

  \[ U_\mathrm{e} = L \frac{\mathrm{d}i}{\mathrm{d}t}. \]

  Z této diferenciální rovnice vyjádříme velikost proudu v závislosti na čase:

  \[ L \frac{\mathrm{d}i}{\mathrm{d}t}= U_\mathrm{e}, \] \[ \frac{\mathrm{d}i}{\mathrm{d}t}= \frac{U_\mathrm{e}}{L}, \] \[ \mathrm{d}i= \frac{U_\mathrm{e}}{L} \mathrm{d}t, \] \[ \int{\mathrm{d}i}= \int{\frac{U_e}{L} \mathrm{d}t },\] \[ i= \frac{U_e}{L} t + C, \]

  kde C je integrační konstanta, kterou určíme z poznatku, že v čase t = 0 s je proud nulový:

  \[ i= \frac{U_\mathrm{e}}{L} t + C, \] \[ 0=0 + C \qquad\Rightarrow\qquad C = 0. \]

  Velikost proudu v závislosti na čase nabývá tedy tvaru:

  \[ i= \frac{U_\mathrm{e}}{L} t. \]

  Až do okamžiku přepálení pojistky tedy proud tekoucí cívkou lineárně roste. Pro čas t_p, ve kterém k tomuto přepálení dojde, bude platit:

  \[ I_\mathrm{max} = \frac{U_\mathrm{e}}{L}t_\mathrm{p},\] \[ t_\mathrm{p}= \frac{L I_\mathrm{max}}{U_\mathrm{e}}, \]

  kde I_max je hodnota proudu, při které dojde k přepálení pojistky.

• b) Řešení – závislost proudu protékajícího cívkou na čase

  Závislost proudu tekoucího cívkou na čase je do přepálení pojistky dána vztahem:

  \[ i(t) = \frac{U_\mathrm{e}}{L} t.\]

  Tuto závislost jsme odvodili v předchozím oddíle.

  Po přepálení pojistky se situace v obvodě změní. Proud začne protékat rezistorem a jeho velikost se bude zmenšovat. Protože ideální cívka má nulový odpor, bude podle Ohmova zákona v ustáleném stavu protékat obvodem proud o velikosti:

  \[ i = \frac{U_\mathrm{e}}{R} = \frac{2}{3}\,\mathrm A, \]

  zatímco v okamžiku přepálení je velikost proudu:

  \[ I_\mathrm{max}= 3\,\mathrm A.\]

  ---

  Řešení této části úlohy je obdobné jako v části a). Napětí, které se bude indukovat v cívce, bude v tomto případě působit proti poklesu proudu. Užitím 2. Kirchhoffova zákona získáváme

  \[ U_\mathrm{e} = Ri(t)+ L \frac{\mathrm{d}i(t)}{\mathrm{d}t}, \]

  kde první člen na pravé straně odpovídá úbytku napětí na rezistoru a druhý člen napětí indukovanému na cívce (díky tomu, že proud klesá, bude jeho derivace záporná a skutečně indukované napětí bude bránit poklesu proudu).

  Výraz upravíme na obvyklý tvar lineární diferenciální rovnice 1. řádu s konstantní pravou stranou:

  \[ L \frac{\mathrm{d}i(t)}{\mathrm{d}t} + Ri(t) = U_\mathrm{e}. \]

  Obecné řešení rovnice tohoto typu můžeme vyjádřit jako součet obecného řešení příslušné diferenciální rovnice bez pravé strany (tzv. homogenní rovnice) a partikulárního řešení.

  Řešením uvedené rovnice zjistíme, že závislost proudu tekoucího cívkou na době, která uplynula od přepálení žárovky, je dána vztahem (podrobný postup je uveden v následujících oddílech):

  \[i(t) = \frac{U_\mathrm{e}}{R} + (I_\mathrm{max} - \frac{U_\mathrm{e}}{R}) e^\mathrm{- \frac{R}{L}t}. \]

• 1.) Obecné řešení homogenní diferenciální rovnice

  Řešíme tedy rovnici ve tvaru:

  \[ L \frac{\mathrm{d}i(t)}{\mathrm{d}t} + Ri(t) = 0, \] \[\frac{\mathrm{d}i(t)}{\mathrm{d}t} + \frac{R}{L}i(t) = 0, \]

  kterou lze řešit např. pomocí metody separace proměnných:

  \[\frac{\mathrm{d}i(t)}{\mathrm{d}t} = - \frac{R}{L}i(t) , \] \[\frac{1}{i(t)}\mathrm{d}i = - \frac{R}{L}\mathrm{d}t , \] \[\int \frac{1}{i(t)}\mathrm{d}i = \int (- \frac{R}{L})\mathrm{d}t , \] \[\ln |i(t)| = - \frac{R}{L}t + k , \]

  kde k je integrační konstanta. Po odlogaritmování a označení C = e^k má řešení homogenní rovnice tvar:

  \[i(t) = C{e}^\mathrm{- \frac{R}{L}t}. \]

• 2.) Partikulární řešení diferenciální rovnice

  K nalezení partikulárního řešení i_p(t) použijeme metodu variace konstanty: Její princip spočívá v předpokladu, že řešení homogenní rovnice bude vyhovovat rovnici úplné, jestliže nahradíme konstantu C vhodnou funkcí. Budeme tedy předpokládat, že:

  \[i_\mathrm{p}(t) = C(t)e^\mathrm{- \frac{R}{L}t} \]

  je hledaným řešením a dosadíme tuto funkci do úplné rovnice.

  Nejdříve si připravíme derivaci této funkce podle času (budeme značit čárkou) jako derivaci součinu:

  \[i_\mathrm{p}(t) = C(t) e^\mathrm{- \frac{R}{L}t}, \] \[i_\mathrm{p}^,(t) = C^,(t) e^\mathrm{- \frac{R}{L}t} - \frac{R C(t)}{L}(t)e^\mathrm{- \frac{R}{L}t}.\]

  Nyní dosadíme tuto funkci a její výše připravenou derivaci do úplné rovnice a vyjádříme neznámou funkci C(t):

  \[ L \frac{\mathrm{d}i_\mathrm{p}(t)}{\mathrm{d}t} + Ri_\mathrm{p}(t) = U_\mathrm{e} ,\] \[ L ( C^,(t) e^\mathrm{- \frac{R}{L}t} - \frac{R C(t)}{L}(t)e^\mathrm{- \frac{R}{L}t}) + R C(t) e^\mathrm{- \frac{R}{L}t}= U_\mathrm{e} \]

  a upravíme

  \[ L C^,(t) e^\mathrm{- \frac{R}{L}t} - R C(t) e^\mathrm{- \frac{R}{L}t} + R C(t) e^\mathrm{- \frac{R}{L}t}= U_\mathrm{e} ,\] \[ L C^,(t) e^\mathrm{- \frac{R}{L}t} = U_\mathrm{e} ,\] \[ C^,(t) = \frac{U_\mathrm{e}}{L} e^\mathrm{ \frac{R}{L}t}.\]

  Zintegrujeme podle času:

  \[ C(t) = \frac{U_\mathrm{e}}{L} e^\mathrm{ \frac{R}{L}t} \frac{L}{R} + K,\] \[ C(t) = \frac{U_\mathrm{e}}{R} e^\mathrm{ \frac{R}{L}t} + K,\]

  kde K je integrační konstanta.

• 3.) Úplné řešení diferenciální rovnice

  Vztah pro funkci C(t) dosadíme do výrazu pro řešení homogenní rovnice a získáme tak obecné řešení úplné rovnice:

  \[i(t) = C(t) e^\mathrm{- \frac{R}{L}t}, \] \[i(t) = \left(\frac{U_\mathrm{e}}{R} e^\mathrm{ \frac{R}{L}t} + K \right)e^\mathrm{- \frac{R}{L}t} \]

  a po úpravě:

  \[i(t) = \frac{U_\mathrm{e}}{R} + K e^\mathrm{- \frac{R}{L}t}. \]

  Integrační konstantu K určíme z počátečních podmínek. V okamžiku přepálení pojistky uvažujeme t = 0 s a proud tekoucí cívkou o velikosti I_max = 3 A. Díky tomu dostáváme:

  \[I_\mathrm{max} = \frac{U_\mathrm{e}}{R} + K, \] \[ K = I_\mathrm{max} - \frac{U_\mathrm{e}}{R}. \]

  Závislost proudu tekoucího cívkou na době, která uplynula od přepálení žárovky, je dána vztahem:

  \[i(t) = \frac{U_\mathrm{e}}{R} + \left(I_\mathrm{max} - \frac{U_\mathrm{e}}{R}\right) e^\mathrm{- \frac{R}{L}t}. \]

  ---

  Pozn.: Pro velmi velké časy bude velikost proudu odpovídat ustálenému proudu, který odpovídá Ohmovu zákonu.

  \[i(t\rightarrow \infty) = \lim_{t\rightarrow \infty}\left[\frac{U_\mathrm{e}}{R} + \left(I_\mathrm{max} - \frac{U_\mathrm{e}}{R}\right) e^\mathrm{- \frac{R}{L}t}\right]\,=\, \frac{U_\mathrm{e}}{R} + \left(I_\mathrm{max} - \frac{U_\mathrm{e}}{R}\right) \cdot 0 = \frac{U_e}{R}.\]

  Odvození naleznete v oddíle b) Řešení – závislost proudu protékajícího cívkou na čase.

• Zápis a číselné dosazení

  Ue = 10 V	elektromotorické napětí zdroje
  L = 5 H	indukčnost cívky
  R = 15 Ω	odpor rezistoru
  Imax = 3 A	maximální hodnota proudu, při které dojde k přepálení pojistky
  tp = ? (s)	čas, za který dojde k přepálení pojistky
  i(t) = ?	závislost proudu tekoucího cívkou na čase

  ---

  Doba, za kterou dojde k přepálení pojistky:

  \[ t_\mathrm{p}= \frac{L I_\mathrm{max}}{U_\mathrm{e}}= \frac{5 {\cdot} 3}{10}\,\mathrm s = 1{,}5 \,\mathrm s. \]

  Závislost proudu tekoucího cívkou na čase před přepálením pojistky:

  \[ i(t) = \frac{U_\mathrm{e}}{L} t = \frac{10}{5} t = 2 t\,\mathrm{A}.\]

  Závislost proudu tekoucího cívkou na čase od přepálení pojistky:

  \[i(t) = \frac{U_\mathrm{e}}{R} + (I_\mathrm{max} - \frac{U_\mathrm{e}}{R}) e^\mathrm{- \frac{R}{L}t} = ( \frac{10}{15} + (3 - \frac{10}{15}) e^\mathrm{- \frac{15}{3}{t}})\,\mathrm A=(\frac{2}{3} + (3 - \frac{2}{3}) e^\mathrm{- 3{t}})\,\mathrm A=(\frac{2}{3} + \frac{7}{3} e^{- 3{t}})\,\mathrm A. \]

  Pozn.: Čas dosazujeme do obou vztahů v sekundách.

• Odpověď

  K přepálení pojistky dojde za 1,5 s. Závislost proudu tekoucího cívkou na čase musíme rozdělit na dva případy – před přepálením pojistky:

  \[ i(t) = 2 t\,\mathrm{A}\]

  a po přepálení pojistky:

  \[i(t) = (\frac{2}{3} + \frac{7}{3} e^\mathrm{- 3t})\,\mathrm A. \]

  Pozn.: Čas dosazujeme do obou vztahů v sekundách.