Sbírka řešených úloh

Intenzita ve vrcholu trojúhelníku

Úloha číslo: 18

• Nápověda 1

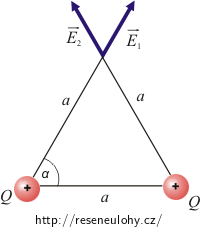
  Celkovou elektrickou intenzitu získáme sečtením intenzit od obou nábojů. Nakreslete si obrázek.

• Nápověda 2

  Elektrická intenzita má stejný směr jako síla, která by v daném místě působila na kladný náboj.

• Obrázek

  

• Rozbor

  Celková elektrická intenzita ve vrcholu trojúhelníka je dána vektorovým součtem intenzit od jednotlivých nábojů.

  Náboje mají stejnou velikost i vzdálenost od místa, kde intenzitu zjišťujeme, proto mají oba vektory intenzity stejnou velikost. Směr elektrické intenzity je stejný jako směr elektrické síly, která by působila na kladný náboj („testovací“ náboj) ve vrcholu trojúhelníka. U kladných nábojů bude tedy intenzita mířit směrem „od“.

• Řešení

  Celkovou intenzitu získáme vektorovým součtem intenzit, které vytváří jednotlivé bodové náboje.

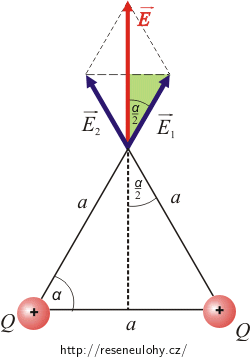
  Intenzity \(\vec{E}_1\) a \(\vec{E}_2\) mají stejnou velikost, protože oba náboje jsou stejně velké a mají stejnou vzdálenost od místa, kde intenzitu měříme. Protože jsou náboje kladné, míří intenzity od nich.

  

  Trojúhelník je rovnostranný, proto známe velikost úhlu α = 60°.

  Ze „zeleného“ pravoúhlého trojúhelníka vyjádříme kosinus úhlu \(\frac{\alpha}{2}:\)

  \[\cos{\frac { \alpha}{2}}\,=\,\frac{\frac {E}{2}}{E_1}\]

  a vyjádříme neznámou celkovou intenzitu E:

  \[E\,=\,2E_1\cos \frac{\alpha}{2}\,.\tag{*}\]

  Intenzitu E₁ spočteme ze vztahu:

  \[E_1\,=\,k \, \frac{Q}{r^2}\, ,\]

  kde r je vzdálenost nábojů. V našem případě jsme si vzdálenost nábojů označili a. Poslední uvedený vztah dosadíme do vzorce (*):

  \[E\,=\,2k\, \frac {Q}{a^2} \,\cos \frac{\alpha}{2}.\]

• Zápis a číselné dosazení

  \[ \begin{eqnarray} a\,&=&\,0{,}5 \,\mathrm{m}\\ Q\,&=&\,1\,\mathrm{\mu C}\,=\,10^{-6}\,\mathrm{C}\\ E\,&=&\,?\,\left(\mathrm{kV\,m^{-1}}\right) \end{eqnarray}\]

  Z tabulek:

  \[k\,=\, 9 {\cdot} 10^9\,\mathrm{kg\,m^2\,s^{-2}\,C^{-1}}\]

  ---

  \[ \begin{eqnarray} E\,&=&\,2k\, \frac {Q}{a^2} \,\cos \frac{\alpha}{2}\\ E\,&=&\,2 \,\cdot \,9 {\cdot} 10^9 \,\cdot\, \frac {10^{-6}}{0{,}5^2}\,\cdot\, \cos \frac{60^\circ}{2}\, \mathrm{V\,m^{-1}}\,=\,\frac{18 {\cdot} 10^3}{0{,}25} \cdot \frac {\sqrt 3}{2}\, \mathrm{V\,m^{-1}}\\ E\,&=&\,6{,}2 {\cdot}10^4 \, \mathrm{V\,m^{-1}}\,=\,62 \, \mathrm{kV\,m^{-1}} \end{eqnarray}\]

• Odpověď

  Ve třetím vrcholu trojúhelníku bude vektor elektrické intenzity směřovat nahoru a bude mít velikost

  \[E\,=\,2k\, \frac {Q}{r^2} \,\cos \frac{\alpha}{2}\,=\,62 \, \mathrm{kVm^{-1}}\,.\]

• Co se změní, budou-li oba náboje záporné?

  Velikost vektoru intenzity \(\vec{E}_1\) a \(\vec{E}_2\) je stále stejná, protože náboje jsou stejně velké a jejich vzdálenost se také nezměnila. Ale směr vektorů bude opačný, protože náboje jsou záporné.

  

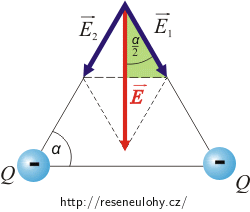
  Další postup výpočtu by byl stejný.

  Celková intenzita by tedy měla stejnou velikost, ale opačný směr, než má pro dva kladné náboje.