Magnetický tok čtvercem
Úloha číslo: 67
Vypočtěte magnetický indukční tok Φ čtvercem o straně 3 cm, který je umístněn v blízkosti dlouhého přímého vodiče, kterým protéká proud 15 A. Jedna strana čtverce je rovnoběžná s vodičem ve vzdálenosti 4 cm. Protilehlá strana je ve vzdálenosti 5 cm od vodiče.
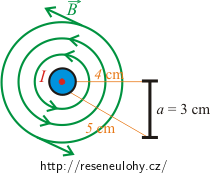
Nápověda
Uvědomte si, jak vypadá vzorec pro magnetický indukční tok plochou smyčky. Díky poloze čtverce a vodiče nebude velikost magnetické indukce v obsahu čtverce konstantní, ale bude se měnit.
Rozbor
Nejdříve si napíšeme vzorec pro magnetický indukční tok Φ. Ve vzorci vystupuje velikost magnetické indukce. Za ní dosadíme vztah pro velikost magnetické indukce dlouhého přímého vodiče.
Díky poloze čtverce bude vzdálenost vodiče a místa, kde určujeme velikost magnetické indukce, různá. Tuto vzdálenost si označíme jako neznámou r, která bude sloužit jako integrační proměnná.
Ve vzorci pro magnetický indukční tok integrujeme přes obsah čtverce S. Rozdělíme si čtverec na menší části se stejnou magnetickou indukcí. Těmito částmi budou úzké obdélníky se stranou a, která je rovnoběžná s vodičem, a stranou dx kolmou na vodič. Z trojúhelníku na obrázku vyjádříme stranu dx pomocí vzdálenosti r.
Další proměnné vystupující ve vzorci pro magnetický indukční tok Φ vyjádříme pomocí obrázku tak, aby v nich vystupovala jako jediná měnící se veličina vzdálenost r.
Obrázek
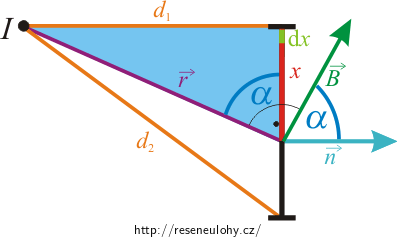
Řešení
Pro magnetický induční tok Φ obsahem plochy S platí vztah:
\[\Phi=\int_\mathrm{S}{B\,\cos{\alpha}}\, \mathrm{d}S.\]V našem případě za velikost magnetické indukce B dosadíme velikost magnetické indukce v okolí dlouhého přímého vodiče:
\[B=\frac{\mu_\mathrm{0}}{2\pi}\, \frac {I}{r},\]kde r je vzdálenost vodiče a místa, kde určujeme velikost magnetické indukce.
Jelikož se vzdálenost r mění v závislosti na místě ve čtverci, použijeme ji jako integrační proměnnou a ostatní veličiny ve vzorci pro magnetický indukční tok Φ vyjádříme pomocí vzdálenosti r.
Za element obsahu plochy dS dosadíme:
\[\mathrm{d}S = a\, \mathrm{d}x,\]kde a je strana čtverce rovnoběžná s vodičem a dx označuje „malou“ část strany čtverce kolmé na vodič, kterou musíme vyjádřit pomocí integrační proměnné r.
Pomocí Pythagorovy věty můžeme z modrého trojúhelníku na obrázku vyjádřit stranu x jako:
\[x=\sqrt{r^{2}-d_1^{2}}.\]Tento vztah zderivujeme a dostaneme:
\[\mathrm{d}x=\frac{r}{\sqrt{r^{2}-d_1^{2}}}\,\mathrm{d}r.\]Získaný výraz dosadíme do výrazu pro element obsahu plochy dS:
\[\mathrm{d}S=\frac{ar}{\sqrt{r^{2}-d_1^{2}}}\,\mathrm{d}r.\]Nyní nám zbývá vyjádřit ve vzorci pro magnetický indukční tok Φ výraz α. Úhel α je úhel mezi směrem magnetické indukce B a kolmicí k ploše. Jak je vidět z obrázku, stejný úhel je také mezi vzdáleností od vodiče r a stranou čtverce x. Cos α si pomocí goniometrických funkcí vyjádříme jako:
\[\cos{\alpha} = \frac {x}{r},\]kde po dosazení výrazu za x dostáváme:
\[\cos{\alpha} = \frac {\sqrt{r^{2}-d_1^{2}}}{r}.\]Nyní již máme vyjádřeny všechny části vzorce pro magnetický indukční tok Φ pomocí jediné proměnné r. Do vzorce pro magnetický indukční tok Φ
\[\Phi=\int_\mathrm{S}{B\,\cos{\alpha}}\, \mathrm{d}S\]můžeme tyto jednotlivé vztahy dosadit:
\[\Phi = \int_\mathrm{d_1}^\mathrm{d_2}{\frac{\mu_\mathrm{0} I}{2\pi r}\,\frac {\sqrt{r^{2}-d_1^{2}}}{r}\,\frac{ar}{\sqrt{r^{2}-d_1^{2}}}}\,\mathrm{d}r. \]Integrujeme v mezích od d1 do d2, ve kterých se mění vzdálenost r části smyčky od vodiče.
Po matematických úpravách vzorce pro magnetický indukční tok Φ dostáváme výraz:
\[\Phi = \frac{a \mu_\mathrm{0} I}{2\pi} \int _\mathrm{d_1}^\mathrm{d_2}{\frac{1}{r}}\,\mathrm{d}r = \frac{a \mu_\mathrm{0} I}{2\pi}\ln{\frac{d_2}{d_1}}.\]Komentář - kontrola vyjádření dS
Provedeme zkoušku, zda jsme dobře určili výraz pro element obsahu plochy dS. Strana čtverce je a = 3 cm. Obsah čtverce S = a2 = 9 cm2.
Element obsahu plochy dS jsme si vyjádřili jako:
\[ \mathrm{d}S=\frac{ar}{\sqrt{r^{2}-d_1^{2}}} \mathrm{d}r.\]Integrací přes meze pro vzdálenost r od d1 do d2 by nám měl obsah plochy čtverce S vyjít také 9 cm2:
\[S = \int_\mathrm{d_1}^\mathrm{d_2}{\frac{ar}{\sqrt{r^{2}-d_1^{2}}}}\, \mathrm{d}r.\]Integrál vyřešíme pomocí substituce:
\[l = r^2 - d_1^{2}\] \[ \mathrm{d}l = 2r\, \mathrm{d}r\] \[ \mathrm{d}r = \frac{ \mathrm{d}l}{2r}.\]Po dosazení a změně mezí integrálu dostáváme výraz:
\[S = \int_0^\mathrm{d_2^{2}-d_1^{2}} {\frac{a}{2}\,\frac{1}{\sqrt{l}}\, \mathrm{d}l} =\frac{a}{2}\left[2\sqrt{l}\right]_0^\mathrm{d_2^{2}-d_1^{2}} =\frac{a}{2}\left(2\sqrt{d_2^{2}-d_1^{2}}-2\sqrt{0}\right).\]Po dosazení číselných hodnot:
\[S=\frac{3}{2}\left(2\sqrt{5^{2}-4^{2}}-2\sqrt{0}\right)\,\mathrm{cm^{2}}= 9\,\mathrm{cm^{2}}.\]Vidíme, že pomocí vyjádření dS jsme dostali správný vztah pro obsah čtverce.
Zápis a číselné dosazení
\(a = 3\,\mathrm{cm} = 0{,}03\,\mathrm{m}\) délka strany čtverce \(I = 15\,\mathrm{A}\) proud protékající vodičem \(d_1=4\,\mathrm{cm}= 0{,}04\,\mathrm{m}\) vzdálenost jedné strany čtverce od vodiče \(d_2=5\,\mathrm{cm}= 0{,}05\,\mathrm{m}\) vzdálenost druhé strany čtverce od vodiče \(\Phi = \mathrm{?}\,\mathrm{(Wb)}\) magnetický indukční tok
\[\Phi = \frac{a\mu_\mathrm{0} I}{2\pi}\ln{\frac{d_2}{d_1}} = \left({ \frac{0{,}03{\cdot} 4\cdot \pi \cdot 10^{-7}\cdot 15}{2\pi}\, \ln {\frac{5}{4}}}\right)\,\mathrm{nWb}\,\dot{=}\, 20 \,\mathrm{nWb}\]Odpověď
Magnetický indukční tok vodivým čtvercem je přibližně Φ = 20 nWb.



