Trojúhelníkový průběh proudu
Úloha číslo: 233
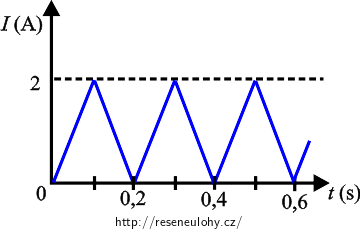
Proud tekoucí rezistorem o hodnotě odporu 100 Ω má periodický trojúhelníkový průběh. Určete:
| a) střední hodnotu proudu, |
| b) efektivní hodnotu proudu, |
| c) průměrný výkon. |
Porovnejte s hodnotami harmonického průběhu proudu se stejnou amplitudou.
Nápověda 1 - definice střední hodnoty proudu
Střední hodnotu proudu definujeme pomocí integrálu:
\[\bar{I}=\frac{1}{T} \int_{0}^\mathrm{T}{i(t)}\,dt.\]Střední hodnota proudu odpovídá výšce obdélníka s délkou strany rovnou periodě a se stejnou plochou, jako je plocha pod časovým průběhem proudu i(t) za jednu periodu.
Nápověda 2
Máme-li trojúhelníkový (= pilovitý) průběh proudu, platí mezi maximální hodnotou proudu a efektivní hodnotou proudu jiný vztah než u sinusového průběhu proudu.
Vztah mezi nimi získáme ze znalosti časového průběhu proudu (pomocí grafu).
Nápověda 3
Uvědomte si, jak vyjádříme výkon v obvodu s proměnným proudem a jak vyjádření výkonu souvisí s definicí efektivních hodnot proudu a napětí.
Rozbor úlohy
a) Střední hodnotu proudu vypočteme pomocí definičního integrálu.
b) Efektivní hodnotu proudu vyjádříme pomocí maximální hodnoty, abychom mohli výsledek porovnat s harmonickým průběhem proudu. Spočteme Jouleovo teplo pro tento průběh proudu uvolněné za jednu periodu. Efektivní hodnota je takový konstantní proud, který za stejný čas uvolní stejné teplo.
c) Výkon získáme ze vztahu pro výpočet výkonu v obvodu s proměnným proudem.
a) Řešení - střední hodnota proudu

Trojúhelníkový průběh proudu je periodický a v průběhu jedné periody je symetrický, jak je vidět z grafu. Proto je plocha pod grafem v obou polovinách periody stejná a můžeme integrál z definice pro výpočet střední hodnoty proudu přepsat na tvar:
\[\bar{I}=\frac{1}{T} \int_{0}^\mathrm{T}{i\left(t\right)}\,dt=2\, \frac{1}{T} \int_{0}^\mathrm{\frac{T}{2}}{i\left(t\right)}\,dt.\]V první půlperiodě můžeme proud i(t) vyjádřit jako:
\[i\left(t\right)=\frac{I_{\mathrm{max}}}{\frac{T}{2}}\,t= \frac{2\,I_{\mathrm{max}}}{T}\,t,\]kde Imax je označení pro maximální hodnotu proudu, která je v grafu naznačena čárkovanou čarou, a (2 Imax)/T je směrnicí přímky určující průběh proudu na první polovině periody.
Nyní dosadíme do vztahu pro výpočet střední hodnoty proudu:
\[\bar{I}=\frac{2}{T} \int_{0}^\mathrm{\frac{T}{2}}{\frac{2\,I_{\mathrm{max}}}{T}\,t}\,dt=\frac{4\,I_{\mathrm{max}}}{T^2} \int_{0}^\mathrm{\frac{T}{2}}\,t\,dt.\]Vypočítáme integrál:
\[\bar{I}=\frac{4\,I_{\mathrm{max}}}{T^2} \int_{0}^\mathrm{\frac{T}{2}}\,t\,dt=\frac{4\,I_{\mathrm{max}}}{T^2} \left[\frac{t^2}{2}\right]_0^\mathrm{\frac{T}{2}}=\frac{4\,I_{\mathrm{max}}}{T^2}\, \frac{\left({\frac{T}{2}}\right)^2}{2}.\]Po úpravě získáme vztah pro výpočet střední hodnoty proudu pro trojúhelníkový průběh:
\[\bar{I}=\frac{I_{\mathrm{max}}}{2}.\]Střední hodnota proudu je tedy rovna polovině maximální hodnoty.
trojuhelnik.page.tagged.png)
Pozn.: Z definice pro střední hodnotu proudu víme, že střední hodnota odpovídá výšce obdélníka s hranou o délce rovné jedné periodě a stejné ploše, jako je plocha pod časovým průběhem proudu. Platnost tohoto tvrzení pro zadaný průběh proudu je ukázána na následujícím obrázku.
trojuhelnik.page.tagged.png)
b) Řešení - efektivní hodnota proudu
Efektivní hodnoty proudu Ief a napětí Uef jsou definovány vztahem:
\[Q= U_\mathrm{ef}\,I_\mathrm{ef}\, t,\]kde Q je Jouleovo teplo uvolněné v obvodu za čas t.
V obvodu máme zapojen pouze rezistor, což znamená, že fázový posun mezi napětím a proudem je nulový. Vztah pro vyjádření Jouleova tepla přepíšeme pomocí Ohmova zákona do tvaru, ve kterém vystupuje pouze efektivní hodnota proudu a odpor:
\[Q=U_\mathrm{ef}\,I_\mathrm{ef}\, t= R\,{\left(I_\mathrm{ef}\right)}^2 \, t.\]Při periodickém průběhu proudu se obvykle za časový úsek t bere perioda T.
Obecně vyjádříme Jouleovo teplo uvolněné v obvodu s proměnným proudem jako:
\[Q=\int_{0}^\mathrm{T}{ui}\,\mathrm{d}t.\]V obvodu je zapojen rezistor, proto si předchozí vztah můžeme také přepsat do tvaru:
\[Q=\int_{0}^\mathrm{T}{Ri^2}\,\mathrm{d}t.\]
Stejně jako v části řešení a) si průběh proudu vyjádříme v první polovině periody jako:
\[i=\frac{2\,I_{\mathrm{max}}}{T} t.\]V druhé polovině periody průběh proudu vyjádříme pomocí vztahu:
\[i=2\,I_{\mathrm{max}}-\frac{2\,I_{\mathrm{max}}}{T} t\,.\]Dosadíme do vyjádření Jouleova tepla za proud:
\[Q=\int_{0}^\mathrm{\frac{T}{2}}{R\left(\frac{2\,I_{\mathrm{max}}}{T} t\right)^2}\,\mathrm{d}t\,+\,\int_\mathrm{\frac{T}{2}}^\mathrm{T}{R\left(\frac{-2\,I_{\mathrm{max}}}{T} t + 2\,I_{\mathrm{max}}\right)^2}\,\mathrm{d}t.\]
Pro přehlednost řešení vypočteme každý z těchto integrálů zvlášť:
A) první půlperioda:
\[\int_{0}^\mathrm{\frac{T}{2}}{R\left(\frac{2\,I_{\mathrm{max}}}{T} t\right)^2}\,\mathrm{d}t={\frac{4RI_{\mathrm{max}}^2}{T^2}}\int_{0}^\mathrm{\frac{T}{2}}t^2\,\mathrm{d}t=\frac{4RI_{\mathrm{max}}^2}{T^2}\,\left[\frac{t^3}{3}\right]_0^\mathrm{\frac{T}{2}}=\frac{4RI_{\mathrm{max}}^2}{T^2}\,\frac{\left({\frac{T}{2}}\right)^3}{3}=\frac{1}{6}\,RI_{\mathrm{max}}^2 T\tag{1}\]B) druhá půlperioda:
\[\int_\mathrm{\frac{T}{2}}^\mathrm{T}{R\left(\frac{-2\,I_{\mathrm{max}}}{T} t + 2\,I_{\mathrm{max}}\right)^2}\,\mathrm{d}t= R\,\int_\mathrm{\frac{T}{2}}^\mathrm{T}{\left(\frac{4\,I_{\mathrm{max}}^2}{T^2} t^2 - \frac{8\,I_{\mathrm{max}}^2}{T} t + 4\,I_{\mathrm{max}}^2\right)}\,\mathrm{d}t=\tag{2}\] \[=4RI_{\mathrm{max}}^2\,\int_\mathrm{\frac{T}{2}}^\mathrm{T}{\left(\frac{1}{T^2}\,t^2\,-\,\frac{2}{T}\,t\,+\,1\right)}\,\mathrm{d}t=4RI_{\mathrm{max}}^2\,\left[\frac{t^3}{3\,T^2}- \,\frac{t^2}{T}\,+\,t\right]_\mathrm{\frac{T}{2}}^\mathrm{T}\] \[=4RI_{\mathrm{max}}^2\,\left(\frac{\frac{7}{8}T^3}{3\,T^2}-\,\frac{\frac{3}{4}T^2}{T}\,+\,\frac{T}{2}\right)=4RI_{\mathrm{max}}^2\,\left(\frac{7\,T}{24}-\,\frac{3}{4}T+\,\frac{1}{2}T\right)=\frac{1}{6}\,RI_{\mathrm{max}}^2T\]
Sečtením těchto dvou integrálů získáme hledané Jouleovo teplo:
\[Q=\frac{1}{6}\,RI_{\mathrm{max}}^2 T\,+\,\frac{1}{6}\,RI_{\mathrm{max}}^2T=\frac{1}{3}\,RI_{\mathrm{max}}^2T.\]
Nyní porovnáme vyjádření pro výpočet Jouleova tepla pomocí efektivní hodnoty s vyjádřením, kde vystupuje maximální hodnota proudu a vyjádříme efektivní hodnotu:
\[R\,{\left(I_\mathrm{ef}\right)}^2 \, T=\frac{1}{3}\,RI_{\mathrm{max}}^2T\] \[{\left(I_\mathrm{ef}\right)}^2 =\frac{1}{3}\,I_{\mathrm{max}}^2\] \[I_\mathrm{ef} =\frac{I_{\mathrm{max}}}{\sqrt{3}}.\]c) Řešení - průměrný výkon
Výkon v obvodu s proměnným proudem je dán vztahem:
\[P=\frac{Q}{t}.\]V obvodu máme zařazen jen rezistor, a tak si vztah přepíšeme do tvaru, kde hodnota odporu rezistoru vystupuje.
\[P=\frac{Q}{t}=\frac{U_\mathrm{ef}\, I_\mathrm{ef}\, t}{t}=U_\mathrm{ef}\, I_\mathrm{ef}=R (I_\mathrm{ef})^2= R \left(\frac{I_{\mathrm{max}}}{\sqrt{3}}\right)^2=\frac{1}{3}RI_\mathrm{max}^2.\]Porovnání pilovitého a harmonického průběhu
Srovnání je uvedeno v následující tabulce. Pro pilovitý průběh jsou uvedeny výsledky, které byly v předchozích sekcích odvozeny.
Pilovitý průběh: Harmonický průběh: Střední hodnota proudu: \[ I=\frac{I_{\mathrm{max}}}{2} \ \,\] \[ I=0 \ \,\] Efektivní hodnota proudu: \[ I_\mathrm{ef}=\frac{I_{\mathrm{max}}}{\sqrt{3}}\ \ \,\] \[ I_\mathrm{ef}=\frac{I_{\mathrm{max}}}{\sqrt{2}}\ \ \,\] Průměrný výkon: \[ P=R\,\frac{I_{\mathrm{max}}^2}{3}\ \ \,\] \[ P=R\,\frac{I_{\mathrm{max}}^2}{2}\ \ \,\] Poznámka: Uvažujeme „běžný“ harmonický průběh, který je např. v rozvodné elektrické síti.
Zápis a číselné dosazení
R = 100 Ω odpor rezistoru Imax = 2 A maximální hodnota proudu T = 0,2 s perioda zdroje \(\bar{I}\) = ? (A) střední hodnota proudu Ief = ? (A) efektivní hodnota proudu P = ? (W) průměrný výkon
\[\bar{I}=\frac{I_{\mathrm{max}}}{2}=\frac{2}{2}\,\mathrm A=1\,\mathrm A\] \[I_{ef} =\frac{I_{\mathrm{max}}}{\sqrt{3}}=\frac{2}{\sqrt{3}}\,\mathrm A\overset{\cdot}{=}1{,}15\,\mathrm A\] \[P= R \left(\frac{I_{\mathrm{max}}}{\sqrt{3}}\right)^2=100\cdot \left(\frac{2}{\sqrt{3}}\right)^2\,\mathrm W\overset{\cdot}{=}133\,\mathrm W \]Odpověď
Střední hodnota zadaného proudu je 1 A.
Efektivní hodnota proudu má velikost přibližně 1,15 A.
Průměrná hodnota výkonu je asi 133 W.


