Pohybující se vodič v magnetickém poli
Úloha číslo: 60
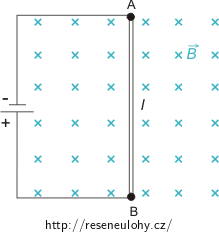
Přímý vodič délky 1 m (AB na obrázku) o odporu 2 Ω se nachází v magnetickém poli o magnetické indukci 0,1 T. Vodič je připojen ke zdroji o napětí 1 V.
a) Určete proud I procházející vodičem, jestliže:
- vodič je v klidu,
- vodič se pohybuje rychlostí 4 m·s-1 vpravo,
- vodič se pohybuje rychlostí 4 m·s-1 vlevo.
b) Kterým směrem a jakou rychlostí se vodič musí pohybovat, aby jím neprocházel žádný proud? Jakým směrem se musí vodič pohybovat, aby jím procházel stejný proud, jako kdyby byl v klidu?
Nápověda
Co musí být splněno, aby se v obvodu indukovalo elektromotorické napětí? Kdy ho budeme k napětí zdroje přičítat a kdy odečítat?
Rozbor a)
Ve smyčce znázorněné na obrázku se indukuje elektromotorické napětí, pokud se mění magnetický indukční tok plochou smyčky. Ten si můžeme představit jako „počet indukčních čar procházejících plochou smyčky“. Velmi důležité je, že nezáleží na celkovém počtu indukčních čar procházejících plochou smyčky, ale pouze na změně jejich počtu. Velikost elektromagnetického napětí a indukovaného proudu závisí na rychlosti změny tohoto počtu. Proto v prvním případě (vodič je v klidu) magnetické pole neovlivní obvod. Proud vypočítáme podle Ohmova zákona.
V druhém případě se vodič pohybuje stálou rychlostí doprava, tím se zvětšuje obsah plochy smyčky, tedy i indukční tok smyčkou. V obvodu se bude indukovat proud, který kolem sebe vytváří magnetické pole. Magnetické indukční čáry tohoto pole budou mít takový směr, aby bránily změně magnetického toku (budou se ho snažit zmenšit). Jejich směr tedy bude opačný než směr vnějšího magnetického pole, tedy k nám. Pomocí Ampérova pravidla určíme směr indukovaného proudu. Vztyčený palec bude znázorňovat směr magnetických indukčních čar a zahnuté prsty směr proudu ve vodiči, který bude mít směr proti směru hodinových ručiček. Směr indukovaného proudu a proudu od baterie je stejný, proto je můžeme sečíst. Obdobně to platí pro napětí, kde celkové napětí je součet indukovaného elektromotorického napětí a napětí baterie.
Ve třetím případě se vodič pohybuje stálou rychlostí doleva, tím se zmenšuje plocha smyčky i „počet indukčních čar smyčkou“. V obvodu se indukuje proud, který kolem sebe vytváří magnetické pole. Magnetické indukční čáry tohoto pole budou mít takový směr, aby bránily změně magnetického toku (budou ho chtít zvětšit). Pomocí Ampérova pravidla opět určíme směr indukovaného proudu, který bude tentokrát po směru hodinových ručiček. Směry indukovaného proudu a proudu od baterie jsou opačné, proto se budou odečítat. Obdobně to platí pro napětí, kde celkové napětí je rozdíl elektromotorického napětí a napětí od baterie.
Řešení a)
V prvním případě se neindukuje žádné elektromotorické napětí, proto proud vypočítáme z Ohmova zákona:
\[U=R I\hspace{15px}\Rightarrow\hspace{15px}I_{\mathrm{klid}}=\frac{U}{R}.\]V druhém případě proud vypočteme také z Ohmova zákona, kde k napětí zdroje U přičteme indukované elekromotorické napětí Ui:
\[I_{\mathrm{vpravo}}=\frac{U+U_\mathrm{i}}{R}.\]Velikost indukovaného elektromotorické napětí se rovná změně magnetického indukčního toku plochou smyčky za čas:
\[U_\mathrm{i}=\frac{\Delta \Phi}{\Delta t}.\]Pro indukční tok platí
\[\Phi =B S \cos \alpha,\]kde α je úhel mezi kolmicí k ploše smyčky a indukčními čarami, v našem případě α = 0° a cos α = 1. Za obsah plochy S dosadíme:
\[S = l v t.\]Pro indukované napětí dostáváme:
\[U_\mathrm{i} = \frac{\Delta (Blvt)}{\Delta t}.\]Využijeme, že v čitateli je až na čas vše konstantní:
\[U_\mathrm{i} = \frac{Blv\Delta t}{\Delta t}=Blv.\]Dosadíme do vzorce pro proud:
\[I_{\mathrm{vpravo}}=\frac{U+Blv}{R}.\]Ve třetím případě proud vypočteme také z Ohmova zákona, ale od napětí zdroje odečteme indukované elekromotorické napětí:
\[I_{\mathrm{vlevo}}=\frac{U-U_\mathrm{i}}{R}.\]Velikost indukovaného napětí závisí na rychlosti změny magnetického indukčního toku. Vodič se v obou situacích pohybuje stejnou rychlostí, proto je velikost elektromotorického napětí stejná jako ve druhém případě:
\[I_{\mathrm{vlevo}}=\frac{U-Blv}{R}.\]Zápis a číselné dosazení a)
\(l = 1\,\mathrm{m}\) délka vodiče \(R=2\,\mathrm{\Omega}\) odpor vodiče \(B=0{,}1\,\mathrm{T}\) magnetická indukce pole \(U=1\,\mathrm{V}\) napětí na vodiči \(I_{\mathrm{klid}}=\mathrm{?}\,\mathrm{(A)} \) proud vodičem, když je vodič v klidu \(I_{\mathrm{vpravo}}=\mathrm{?}\,\mathrm{(A)} \) proud vodičem, když se vodič pohybuje vpravo \(I_{\mathrm{vlevo}}=\mathrm{?}\,\mathrm{(A)} \) proud vodičem, když se vodič pohybuje vlevo
\[I_{\mathrm{klid}}=\frac{U}{R}=\frac{1}{2}\,\mathrm{A}=0{,}5\,\mathrm{A}\] \[I_{\mathrm{vpravo}}=\frac{U+U_\mathrm{i}}{R}=\frac{U+Blv}{R}=\frac{1+0{,}1{\cdot}1\cdot4}{2}\,\mathrm{A}=0{,}7\,\mathrm{A}\] \[I_{\mathrm{vlevo}}=\frac{U-U_\mathrm{i}}{R}=\frac{U-Blv}{R}=\frac{1-0{,}1{\cdot}1\cdot4}{2}\,\mathrm{A}=0{,}3\,\mathrm{A}\]Odpověď a)
Jestliže je vodič v klidu, prochází jím proud 0,5 A.
Jestliže se vodič pohybuje rychlostí 4 m·s-1 doprava, prochází vodičem proud 0,7 A.
A pokud se vodič pohybuje rychlostí 4 m·s-1 doleva, prochází jím proud 0,3 A.
Rozbor b)
Aby vodičem neprocházel žádný proud, musí být napětí, které se v obvodu indukuje, stejně velké jako napětí od zdroje.
Aby vodičem procházel stejný proud jako v klidu, nesmí se měnit magnetický indukční tok smyčkou, tedy „počet indukčních čar procházejících smyčkou vodiče“. Vodič se tedy může pohybovat pouze ve směru indukčních čar.
Řešení b)
Z Ohmova zákona si vyjádříme proud:
\[I=\frac{U\pm U_\mathrm{i}}{R}.\]Aby obvodem neprocházel žádný proud, musí být napětí, které se v obvodu indukuje, stejně velké jako napětí zdroje:
\[U=U_\mathrm{i}.\]Za elektromotorické napětí dosadíme vztah odvozený v předchozí části:
\[U=U_\mathrm{i}=Bvl.\]Vyjádříme neznámou rychlost v:
\[v=\frac {U}{Bl}.\]Směr pohybu smyčky určíme z řešení a), kde se při pohybu doleva proud zmenšoval, tedy se blížil nule. V našem případě se vodič bude pohybovat doleva rychlostí v.
Kdyby se vodič pohyboval rychlostí větší než rychlost v směrem doleva, indukované napětí by bylo větší než napětí od zdroje a celkový proud vodičem by byl záporný (protékal by opačným směrem).
Zápis a číselné dosazení b)
\(l = 1\,\mathrm{m}\) délka vodiče \(R=2\,\mathrm{\Omega}\) odpor vodiče \(B=0{,}1\,\mathrm{T}\) magnetická indukce pole \(U=1\,\mathrm{V}\) napětí na vodiči \(I=0 \,\mathrm{A}\) proud tekoucí vodičem \(v=\mathrm{?} \) velikost rychlosti pohybu vodiče
\[v=\frac{U}{Bl}=\frac{1}{0{,}1{\cdot} 1}\,\mathrm{m\,s}^{-1}=10\,\mathrm{m\,s}^{-1}\ \]Odpověď b)
Aby vodičem neprocházel proud, musí se pohybovat rychlostí 10 m·s-1 směrem doleva.
Aby vodičem procházel stejný proud jako v klidu, musí se pohybovat ve směru indukčních čar.



