Odpor vodiče v závislosti na teplotě

Úloha číslo: 92

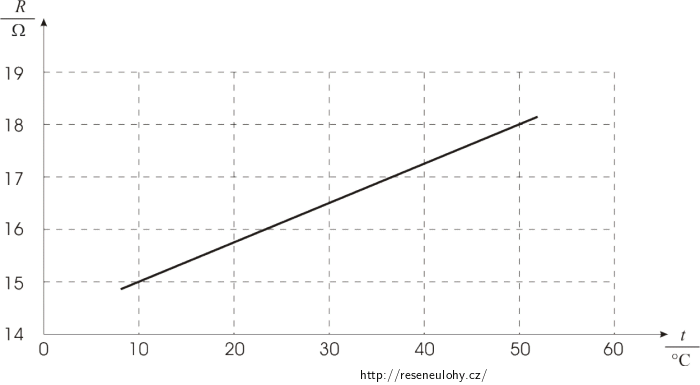
V grafu je zakreslena závislost odporu kovového vodiče na teplotě.

Jaký odpor má vodič při teplotě 20 °C a 40 °C?

Jakou teplotu má vodič, jestliže jeho odpor je 15 Ω, 16,5 Ω a 18 Ω?

Vypočtěte teplotní součinitel elektrického odporu tohoto vodiče. O jaký kov se pravděpodobně jedná?

Nápověda 1
Uvědomte si, jak vypadá závislost odporu elektrického vodiče na teplotě. Čím je tato závislost charakterizována?
Řešení nápovědy 1
Pro „běžné vodiče“ platí, že při zvyšující se teplotě roste i elektrický odpor vodiče. Tento nárůst je pro malé teplotní rozdíly prakticky lineární. Závislost elektrického odporu na teplotě udává vztah:
\[R\,=\,R_0\,\left(1\,+\,\alpha\,\mathrm{\Delta}t\right)\,,\]
kde R je odpor vodiče při teplotě t, R₀ odpor při vztažné teplotě t₀, α je teplotní součinitel elektrického odporu a Δt rozdíl teplot t - t₀.
Nápověda 2
Teplotní součinitel elektrického odporu pro různé materiály najdeme v tabulkách.
Rozbor
Elektrický odpor kovového vodiče závisí na teplotě vodiče a pro „běžné vodiče“ platí, že s rostoucí teplotou se odpor vodiče zvyšuje. Pro nepříliš velké teplotní rozdíly Δt je tento nárůst prakticky lineární.

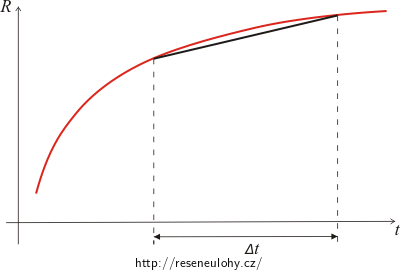
Můžeme tedy říci, že přírůstek elektrického odporu je přímo úměrný rozdílu teplot po zahřátí a před zahřátím vodiče.

Navíc změna odporu závisí i na materiálu, z kterého je vodič vyroben. Konstantu úměrnosti nazýváme teplotní součinitel elektrického odporu α. Jeho jednotkou je K^-1. Hodnoty α jsou závislé na volbě počáteční (tzv. vztažné) teploty. Vztažná teplota se obvykle volí 0 °C.

Změna velikosti teplotního součinitele elektrického odporu se však projeví až při velké změně vztažné teploty.
Odečet hodnot z grafu
Pokud známe teplotu vodiče, můžeme příslušné hodnoty elektrického odporu odečíst z grafu:

Při teplotě 20 °C je odpor vodiče 15,75 Ω

40 °C 17,25 Ω

Stejně tak známe-li hodnoty elektrického odporu, zjistíme z grafu teplotu vodiče:

Při odporu 15 Ω je teplota vodiče 10 °C

16,5 Ω 30 °C

18 Ω 50 °C
Výpočet teplotního součinitele elektrického odporu
Pro závislost elektrického odporu vodiče na teplotě platí vztah:
\[R\,=\,R_0\left(1+\alpha \Delta t\right)\,,\]
kde R je odpor vodiče při teplotě t, R₀ odpor při vztažné teplotě t₀, α je teplotní součinitel elektrického odporu a Δt rozdíl teplot Δt = t − t₀.

Z tohoto vzorce si vyjádříme teplotní součinitel elektrického odporu α:
\[\frac{R}{R_0}\,=\,1+\alpha \Delta t\] \[\alpha \Delta t\,=\,\frac{R}{R_0}-1\,=\,\frac{R-R_0}{R_0}\,.\]
Pro teplotní součinitel elektrického odporu jsme tedy získali rovnici:
\[\alpha\,=\,\frac{R-R_0}{R_0\Delta t}\,.\]
Číselné dosazení:

Z grafu jsme zjistili, že při teplotě 10 °C má vodič odpor 15 Ω a při teplotě 50 °C odpor 18 Ω. Jako vztažnou teplotu vezmeme hodnotu t₀ = 10 °C:
\[t_0\,=\,10\,^{\circ} \mathrm{C}\] \[R_0\,=\,15\,\mathrm{\Omega}\] \[t\,=\,50\,^{\circ} \mathrm{C}\] \[R\,=\,18\,\mathrm{\Omega}\,.\]
Protože stupeň Celsia není základní jednotkou SI, vyjádříme si rozdíl teplot ve stupních Kelvina.

Pro Celsiovu a termodynamickou teplotu platí:
\[\Delta t\,=\,\Delta T\] \[\Delta t\,=\,t-t_0\,=\,40\,^{\circ} \mathrm{C}\,=\,40\,\mathrm{K}\,.\]
Nyní již dosadíme do vzorce číselné hodnoty a vypočítáme teplotní součinitel elektrického odporu:
\[\alpha\,=\,\frac{R-R_0}{R_0\Delta t}\,=\,\frac{\left(18-15\right)\mathrm{\Omega}}{15\mathrm{\Omega}\cdot40\mathrm{K}}\,=\,\frac{3}{15{\cdot} 40}\,\mathrm{K^{-1}}\,=\,5{\cdot}10^{-3}\,\mathrm{K^{-1}}\,.\]
Z tabulek zjistíme, že tato hodnota dobře odpovídá oceli.
Odpověď
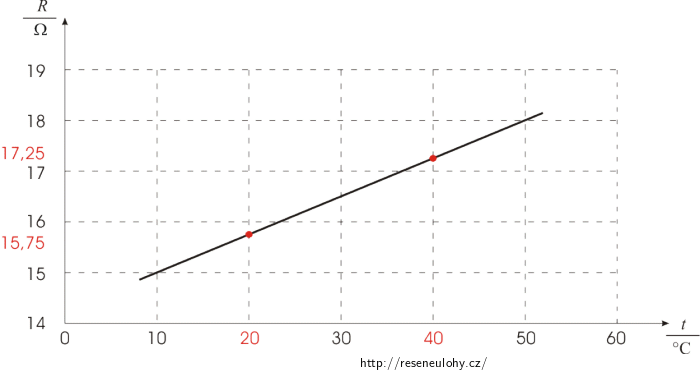
Jestliže má vodič teplotu 20 °C, pak jeho odpor je 15,75 Ω. Při teplotě 40 °C je odpor vodiče 17,25 Ω.

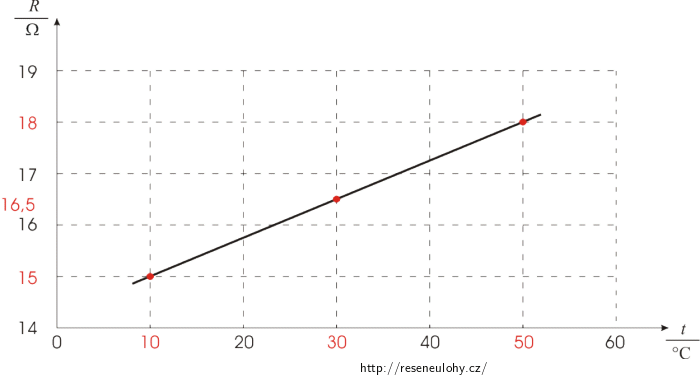
Je-li odpor vodiče 15 Ω, pak jeho teplota je 10 °C. Při odporu 16,5 Ω má vodič teplotu 30 °C a je-li odpor vodiče 18 Ω, pak je jeho teplota 50 °C.

Teplotní součinitel elektrického odporu vodiče je 5·10^-3 K^-1. To je hodnota, která odpovídá ocelovému vodiči.
Odkaz na podobnou úlohu
Podobná úloha, která řeší závislost elektrického proudu na teplotě, je úloha Termistor.