Rovnoběžné vodiče protékané proudy

Úloha číslo: 765

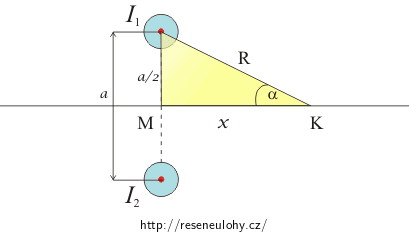
Dvěma nekonečně dlouhými přímými rovnoběžnými vodiči tečou proudy I₁ a I₂. Magnetická indukce v bodě M je rovna nule a v bodě N je orientována podle obrázku. Určete:

a) směry proudů v obou vodičích,

b) poměr velikostí těchto proudů,

c) orientaci magnetické indukce v bodě L,

d) polohu bodu na ose x, v němž je velikost magnetické indukce maximální.

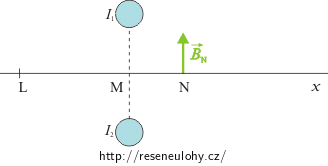
Nápověda a), c)
Při řešení úlohy využijte Ampérovo pravidlo pravé ruky, abyste určili směr indukčních čar v okolí vodiče s proudem.
Ampérovo pravidlo pravé ruky
Palec pravé ruky dáme tak, aby ukazoval směr elektrického proudu ve vodiči. Pokrčené prsty pak ukazují orientaci magnetických indukčních čar v okolí vodiče.
Řešení a) a b)
Kdyby měly proudy v obou vodičích navzájem opačný směr, měly by v souladu s Ampérovým pravidlem pravé ruky vektory magnetické indukce vyvolané těmito vodiči v bodě M stejný směr, a proto by celková indukce v tomto bodě nemohla být rovna nule. Proto musí mít proudy ve vodičích stejný směr.

Ze skutečnosti, že v bodě N je indukce orientována vzhůru, pak opět pomocí pravidla pravé ruky zjistíme, že směr proudu v obou vodičích musí mířit ven z obrázku (tj. směrem k nám). Vektory \(\vec B_1\) a \(\vec B_2\) mají směr tečen ke kružnicím, které reprezentují magnetické pole v okolí jednotlivých vodičů. To, že celková indukce v bodě N je orientována vzhůru, znamená, že magnetické indukce vyvolané oběma vodiči mají stejnou velikost, jak je vidět z obrázku.

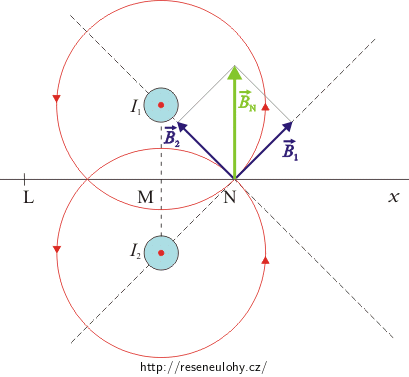
Když přihlédneme ke tvaru vzorce pro výpočet celkové magnetické indukce v okolí nekonečně dlouhého přímého vodiče \( B\,=\,\frac{\mu_{0}I}{2\pi R}\) (odvozeno v úloze Magnetické pole dlouhého přímého vodiče s proudem), je zřejmé, že i proudy v obou vodičích musí mít stejnou velikost.

Došli jsme tak k závěru, že směr proudů je ven z obrázku směrem k nám a proudy mají stejnou velikost.
Řešení c)
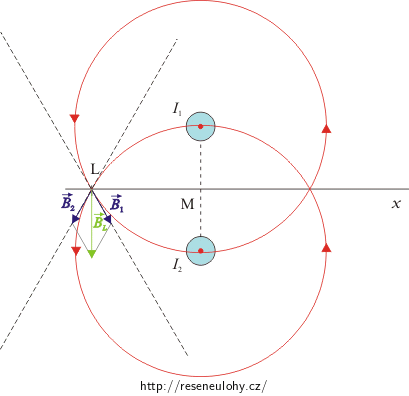
Orientaci magnetické indukce v bodě L určíme opět pomocí Ampérova pravidla pravé ruky – při určeném směru a stejné velikosti proudů ve vodičích zjistíme, že indukce v tomto bodě je orientována směrem dolů (viz obrázek).
Nápověda d)
Nakreslete si obrázek situace. Uvědomte si, že příspěvky k celkové velikosti magnetické indukce na ose x mají pro oba vodiče stejnou velikost. Cílem je vyjádřit velikost celkové magnetické indukce \(\vec B\) v obecném místě na ose x – označme si toto místo třeba jako bod K.
Řešení nápovědy d)

Pro výpočet celkové magnetické indukce v bodě K potřebujeme vyjádřit vzdálenost R bodu K od vodiče. K tomu využijeme žlutý trojúhelník na obrázku a pomocí Pythagorovy věty můžeme psát: \[R= \sqrt {\left(\frac{a}{2}\right)^2+x^2}.\] Pro úhel α platí: \[ \cos {\alpha}= \frac{x}{R}=\frac{x}{\sqrt{ \left(\frac{a}{2}\right)^2+x^2}}.\]
Řešení d)
Podle řešení a) a b) můžeme říci, že příspěvek k velikosti celkové magnetické indukce od obou vodičů bude stejný ve všech bodech na ose x. V bodě M je magnetická indukce nulová, proto ho zvolíme za počátek. Využijeme vzorec pro výpočet magnetické indukce nekonečně dlouhého přímého vodiče \( B\,=\,\frac{\mu_{0}I}{2\pi R}\) a vztahů v žlutém trojúhelníku na obrázku.
\[R= \sqrt {\left(\frac{a}{2}\right)^2+x^2}\] \[\cos {\alpha}=\frac{x}{\sqrt {\left(\frac{a}{2}\right)^2+x^2}}\]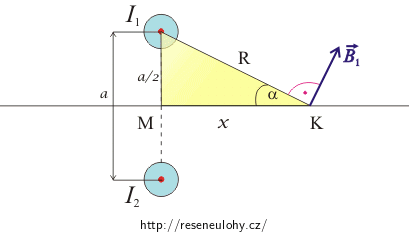

Nyní výše uvedené poznatky spojíme a pro velikosti magnetických indukcí od horního vodiče B₁ a od spodního vodiče B₂ v bodě K napíšeme:
\[ {B_1}\, = {B_2}\,=\, \frac {\mu_0 I}{2\pi\sqrt{\left(\frac{a}{2}\right)^2 + x^2}}.\]
Pomocí obrázku dojdeme ke vztahu určujícímu velikost celkové magnetické indukce B. Na obrázku máme nakreslený příspěvek pouze od jednoho vodiče, pro druhý je to analogické.

Pro velikost celkové indukce B v bodě K potom můžeme psát: \[{B}\,= B_1 \cos{\alpha}+B_2 \cos{\alpha}\,={2 B_1 \cos{\alpha}},\] což po dosazení dává \[B=2 \frac{\mu_0 I}{2 \pi \sqrt{\left(\frac{a}{2}\right)^2+x^2}} \frac{x}{\sqrt{\left(\frac{a}{2}\right)^2+x^2}}\,=\frac{4\mu_0 x I}{\pi(a^2+4 x^2)}.\]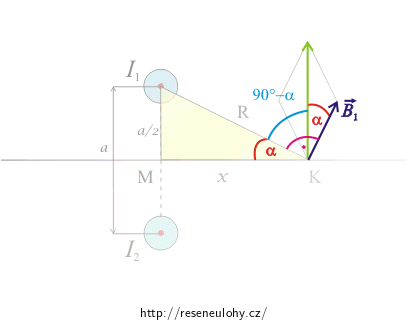
Tím jsme získali vztah udávající závislost velikosti magnetické indukce B na souřadnici x. Tato funkce je spojitá, pro x = 0 a pro x jdoucí k nekonečnu nulová, proto musí mít na tomto intervalu extrém. Pro určení extrému tuto funkci musíme derivovat a derivaci položit rovnu nule. Derivovat budeme jako podíl:
\[\frac{\mathrm{d}B}{\mathrm{d}x}=\frac{4 \mu_0 I \pi (a^2+4 x^2)-4 \mu_0 I x 8 \pi x}{\pi^2(a^2+4 x^2)^2}=\frac{4\mu_0 I\pi(a^2-4 x^2)}{\pi^2(a^2+4 x^2)^2}.\] Poté položíme derivaci rovnu nule a zjistíme polohu extrému: \[\frac{\mathrm{d}B}{\mathrm{d}x}\,=\,0\,\,\Rightarrow\, a^2-4 x^2\,=\,0\,\,\Rightarrow\, 4 x^2\,=\,a^2\,\,\Rightarrow\,x\,=\, ^+_-\frac{a}{2}.\]
Odpověď
Proudy v obou vodičích směřují ven z obrázku směrem k nám a jejich velikost je stejná.

Magnetická indukce v bodě L míří směrem dolů.

Maximální velikost indukce na ose x je ve vzdálenosti \(x =\, ^+_-\frac {a}{2}\) od bodu M.
Graf průběhu magnetické indukce podél osy x
Graf je sestrojen tak, že pokud míří magnetická indukce nahoru, považujeme ji za kladnou, pokud míří dolů, považujeme ji za zápornou.

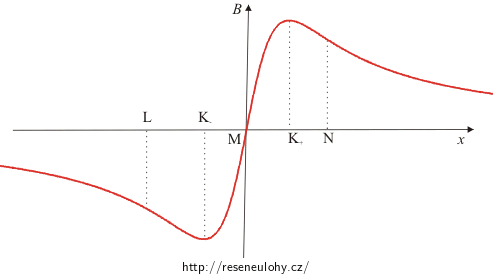
Ve velké vzdálenosti je velikost celkové magnetické indukce velmi malá, protože příspěvky od každého z vodičů jsou malé; když se přibližujeme k vodičům, roste. Zároveň se ale zvětšuje úhel mezi oběma příspěvky. Ve velké vzdálenosti jsou oba téměř rovnoběžné a sčítají se, uprostřed mezi vodiči mají opačné směry a odečítají se, proto je tam indukce nulová. Díky těmto dvěma protichůdným vlivům na velikost celkové magnetické indukce B víme, že v bodě K musí být extrém.