Tři rovnoběžné vodiče s proudem
Úloha číslo: 52
Tři dlouhé přímé vodiče a, b, c protínající kolmo nákresnu v bodech A, B, C jsou ve vzájemné vzdálenosti 10 cm. Prochází jimi stejný proud 100 A. Směry proudů ve vodičích jsou naznačeny na obrázku. Určete velikost síly, která působí na část každého vodiče o délce 1 m.
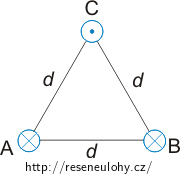
Nápověda
Rozmyslete si, kdy se dva vodiče s proudem přitahují a kdy odpuzují. Nakreslete si síly, kterými na sebe vodiče vzájemně působí.
Rozbor
Dva rovnoběžné vodiče, jimiž protéká elektrický proud, na sebe navzájem silově působí.
Vodiče se souhlasně orientovanými proudy se přitahují, vodiče s opačně orientovanými proudy se odpuzují.
Jelikož všemi vodiči prochází stejně velký proud a vzájemná vzdálenost vodičů je také stejná, působí na sebe libovolné dva vodiče silou o stejné velikosti.
Tuto sílu zjistíme ve dvou krocích:
(1) určíme velikost magnetické indukce B, kterou vytváří druhý vodič v místě prvního vodiče,
(2) určíme sílu, kterou pole o indukci B působí na první vodič.
Výsledná síla působící na vodič se rovná vektorovému součtu obou sil, kterými na tento vodič působí zbývající dva vodiče.
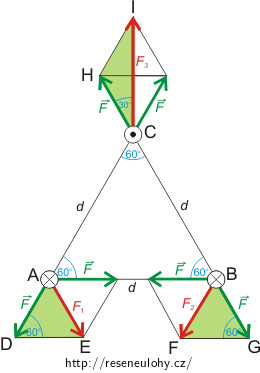
Obrázek
Řešení
Ve vzdálenosti d od vodiče A vzniká magnetické pole o magnetické indukci
\[B_{\mathrm{A}}= \mu_\mathrm{0} \frac {I_{\mathrm{A}}}{2\pi d}.\]V tomto poli se nachází vodič B kolmý na magnetickou indukci BA. Působí na něj magnetická síla FAB:
\[F_{\mathrm{AB}}=B_{\mathrm{A}} I_{\mathrm{B}}l.\]Vodič A tedy působí na vodič B silou
\[F_{\mathrm{A}} = \mu_\mathrm{0} \frac {I_{\mathrm{A}} I_{\mathrm{B}} l}{2 \pi d}.\]Stejně velkou silou působí vodič B na vodič A (3. Newtonův zákon).
Jelikož jsou proudy procházející vodiči i vzájemné vzdálenosti vodičů stejné, působí na sebe vodiče silami o stejné velikosti. Velikost síly označíme F:
\[F=\frac{\mu_\mathrm{0}}{2\pi}\frac{I^{2}}{d} l.\]Směry, ve kterých síly působí, jsou zakresleny na obrázku. Z něj vidíme, že trojúhelníky ADE a BFG jsou rovnostranné, pro velikost sil F1 a F2 vyplývá
\[F_{\mathrm{A}}=F_{\mathrm{B}}=F.\]Po dosazení vztahu pro sílu F získáme
\[F_{\mathrm{A}}=F_{\mathrm{B}}=\frac{\mu_0}{2\pi}\frac{I^{2}}{d} l.\]Vztah pro velikost síly F3 dostaneme z trojúhelníku CHI:
\[F_{\mathrm{C}}=2 F\,\cos\,30^{\mathrm{\circ}}=2F\frac{\sqrt{3}}{2}=\sqrt{3}F.\]Po dosazení vztahu pro sílu F:
\[F_{\mathrm{C}}=\frac{\sqrt{3}\mu_0}{2\pi}\frac{I^2}{d} l.\]Zápis a číselné dosazení
\(d=10 \,\mathrm{cm} = 0{,}10\,\mathrm{m}\) vzdálenost vodičů \(I_{\mathrm{A}} = I_{\mathrm{B}} = I_{\mathrm{C}} =100\,\mathrm{A}\) prod tekoucí vodiči \(l=1\,\mathrm{m}\) délka vodičů \(F_{\mathrm{A}} = ?\,\mathrm{(N)}\) síla působící na vodič A \(F_{\mathrm{B}} = ?\,\mathrm{(N)}\) síla působící na vodič B \(F_{\mathrm{C}} = ?\,\mathrm{(N)}\) síla působící na vodič C Z tabulek: \(\mu_0 = 4\pi \cdot 10^{-7}\,\mathrm{NA^{-2}} \) permeabilita vakua
\[F_{\mathrm{A}}=F_{\mathrm{B}}=\frac{\mu_0}{2\pi}\frac{I^2}{d} l=\frac{4\pi\cdot 10^{-7}}{2\pi}\,\frac{100^2}{0{,}1} 1\,\mathrm{N}=0{,}02\,\mathrm{N}=20\,\mathrm{mN}\] \[F_{\mathrm{C}}=\frac{\sqrt{3}\mu_0}{2\pi}\frac{I^2}{d} l=\frac{\sqrt{3}4\pi 10^{-7}}{2\pi}\,\frac{100^2}{0{,}1} 1\,\mathrm{N}\,\dot{=}\, 0{,}0346\,\mathrm{N} \,\dot{=}\, 35\,\mathrm{mN}\]Odpověď
Na rovnoběžné vodiče s proudem působí síly o velikostech F1 = 20 mN, F2 = 20 mN a F3 =35 mN.


