Elektron v urychlovači
Úloha číslo: 58
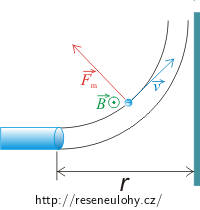
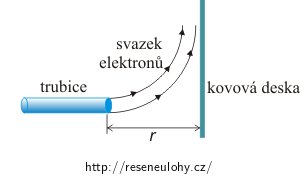
Elektrony s kinetickou energií Ek vylétají z urychlovače. Ve vzdálenosti r od urychlovače se nachází kovová destička umístěná kolmo ke svazku vylétávajících elektronů (viz obrázek). Dokažte, že můžeme zabránit tomu, aby svazek dopadl na destičku, jestliže ho odchýlíme magnetickým polem \(\vec{B}\) o velikosti
\[B=\sqrt{\frac{2mE_\mathrm{k}}{e^{2}r^{2}}},\]kde m a e jsou hmotnost a velikost náboje elektronu. Jak musí být vektor magnetické indukce orientován?
Nápověda
Paprsek elektronů odchýlí magnetická síla, která je kolmá na směr pohybu a působí tedy jako síla dostředivá.
Rozbor
Bez přítomnosti magnetického pole se budou elektrony vylétavající z urychlovače dále pohybovat rovnoměrně přímočaře a narážet na kovovou destičku. Chceme-li zabránit dopadu paprsků na destičku, musíme elektrony vychýlit z jejich původního směru.
Paprsek elektronů vychýlíme tak, že ho necháme procházet magnetickým polem. Když se nabité částice (proud částic) pohybují v magnetickém poli, působí na ně magnetická síla. Ta je kolmá na směr pohybu, působí tedy jako síla dostředivá a zakřivuje trajektorii částic. Částice se budou v magnetickém poli pohybovat po kružnici.
Velikost magnetické indukce vyjádříme ze vztahu pro magnetickou a dostředivou sílu a porovnáme se zadaným vztahem.
Při určování směru magnetické indukce využijeme tohoto poznatku: Jestliže je vektor rychlosti kolmý na vektor magnetické indukce, potom působící síla na částici je maximální a její vektor je kolmý na vektor magnetické indukce. V naší úloze z tohoto poznatku vyplývá, že vektor magnetické indukce bude kolmý k rovině obrázku (viz obrázek v dalším oddíle). Nyní stačí určit, zda bude orientován před nebo za obrázek. To určíme buď pomocí Flemingova pravidla levé ruky, nebo pomocí pravidla pravotočivého šroubu.
Řešení
Uvažujme, že v magnetickém poli o magnetické indukci \(\vec{B}\) se pohybuje částice s nábojem e rychlostí o velikosti v. Je výhodné, aby vektor rychlosti byl kolmý na vektor magnetické indukce. Potom působí na částici maximální magnetická síla \(\vec{F}_m\) a pro její velikost platí
\[F_\mathrm{m} = evB.\]Magnetická síla \(\vec{F}_\mathrm{m}\) působí kolmo na směr pohybu, působí tedy jako síla dostředivá. Díky tomu se částice v tomto magnetickém poli pohybuje po kružnici. Pro velikost dostředivé síly platí vztah:
\[F_\mathrm{d}=m\frac{v^2}{r}.\]Obě vyjádřené síly porovnáme
\[F_\mathrm{m}=F_\mathrm{d},\] \[evB=\frac{mv^2}{r}\]a vyjádříme velikost magnetické indukce B
\[B=\frac{mv}{re}.\]Jelikož neznáme velikost rychlosti elektronů v, určíme ji ze zadané kinetické energie Ek:
\[E_\mathrm{k}=\frac{1}{2} mv^2\hspace{15px}\Rightarrow \hspace{15px} v=\sqrt{\frac{2E_\mathrm{k}}{m}}.\]A dosadíme do vzorce pro velikost magnetické indukce B:
\[B=\frac{m}{re}\sqrt{\frac{2E_\mathrm{k}}{m}}.\]Upravíme a dostaneme výraz, který se shoduje s výrazem v zadání:
\[B=\sqrt{\frac{2mE_\mathrm{k}}{r^2e^2}}.\]Určování směru magnetické indukce B
Orientaci vektoru magnetické indukce můžeme určit pomocí:
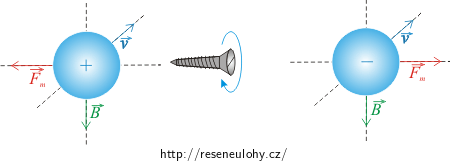
1) Flemingova pravidla levé ruky
Položíme-li k vodiči levou ruku tak, aby natažené prsty ukazovaly směr proudu a magnetické indukční čáry (respektive vektor \(\vec{B}\)) vstupovaly do dlaně, ukazuje odtažený palec směr a orientaci vektoru magnetické síly \(\vec{F}_\mathrm{m}\), která působí na vodič.
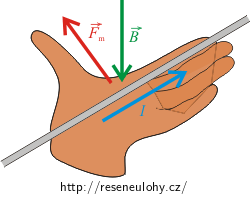
Směr proudu ve vodiči je směr pohybu kladných částic. V našem příkladě jde o proud elektronů, tedy záporných částic. Proto budeme prsty levé ruky orientovat proti směru pohybu paprsku elektronů. Podle obrázku v zadání jsou elektrony vychylovány směrem nahoru, tím směrem působí i magnetická síla. Vektor magnetické indukce musí tedy mířit před obrázek.
2) Pravidlo pravotočivého šroubu
Otáčíme-li pravotočivým šroubem od směru vektoru rychlosti \(\vec{v}\) k směru vektoru magnetické indukce \(\vec{B}\) (nutno otočit o úhel, který je menší než \(\pi\)), šroub se zavrtává ve směru síly \(\vec{F}_\mathrm{m}\) působící na kladný náboj. Pokud je náboj záporný, směr síly \(\vec{F}_\mathrm{m}\) je opačný.
Použijeme-li toto pravidlo, dostáváme stejný směr magnetické indukce \(\vec{B}\) jako výše.
Zápis a číselné dosazení
\(E_\mathrm{k}=5 \,\mathrm{keV}\) — elektron urychlený napětím 5000 VDo vyjádřeného výrazu budeme dosazovat energii v jednotkách Joule.
\(E_\mathrm{k}=8{\cdot} 10^{-16}\,\mathrm{J}\) kinetická energie elektronů \(r=5\,\mathrm{mm}=5 {\cdot} 10^{-3}\,\mathrm{m}\) vzdálenost kovové destičky od urychlovače \(B\,=\,?\,\mathrm{(T)}\) velikost magnetické indukce Z tabulek: \(m_\mathrm{e}=9{,}1 {\cdot} 10^{-31}\,\mathrm{kg}\) hmotnost elektronu \(e=1{,}6{\cdot} 10^{-19}\,\mathrm{C}\) elementární elektrický náboj
\[B=\sqrt{\frac{2mE_\mathrm{k}}{e^{2}r^{2}}}=\sqrt{\frac{2{\cdot} 9{,}1{\cdot} 10^{-31}\cdot8{\cdot} 10^{-16}}{\left(1{,}6{\cdot} 10^{-19}\right)^{2}\left(5 {\cdot} 10^{-3}\right)^{2}}}\,\,\,\mathrm{T}\,\dot{=}\,0{,}048\,\mathrm{T}\dot{=}\,48\,\mathrm{mT}\]Odpověď
Dokázali jsme, že můžeme zabránit tomu, aby svazek dopadal na destičku, pokud ho odchýlíme magnetickým polem o velikosti
\[B=\sqrt{\frac{2mE_\mathrm{k}}{e^{2}r^{2}}}.\]Pro zadané číselné hodnoty je velikost magnetického pole přibližně rovna
\[B\,\dot{=}\,48\,\mathrm{mT}.\]Směr vektoru magnetické indukce bude mířit před obrázek.
Komentář
Z válcové symetrie úlohy je patrné, že jakákoliv orientace magnetické indukce kolmo ke směru svazku elektronů je vhodná.
V naší úloze jsme si zvolili jeden ze směrů vylétávajících svazků elektronů a tedy, že elektrony jsou vychylovány směrem nahoru. Proto musí magnetická indukce, která tento svazek vychyluje, mířit před obrázek.