Dva čtvercové závity protékané proudem
Úloha číslo: 798
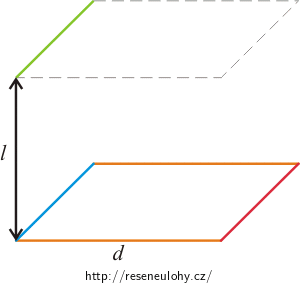
Ve dvou vodorovných rovinách, jejichž vzdálenost je 3 cm, jsou nad sebou dva stejné čtvercové závity o straně 4 cm. Oběma závity prochází proud 3 A.
Určete:
a) směry proudů v závitech, jestliže se závity odpuzují,
b) velikost síly, kterou se závity odpuzují.
Nápověda 1
Vyberte si jednu stranu jednoho ze závitů. Stačí určit, jakou silou tuto stranu odpuzuje druhý závit, síly na ostatní strany budou díky symetrii stejné a můžeme je složit.
Nápověda 2
Navzájem kolmé vodiče na sebe navzájem silově nepůsobí. Co můžeme říct o silách, které působí na vybranou stranu?
Nápověda 3
Uvědomte si, že pole podél jedné strany nebude homogenní. Návod na to, jak průběh pole podél strany spočítat, naleznete v oddíle úlohy Magnetické pole dlouhého přímého vodiče s proudem, Řešení 2.
Nápověda 4
Máme nehomogenní pole v okolí jedné strany čtverce. Díky tomu, že všechny příspěvky k síle mají stejný směr, můžeme velikost síly F spočítat integrací podél strany d \[F=\int_0 ^{d} {B(x)} I \,\mathrm dx,\] kde B(x) je závislost velikosti magnetické indukce B na vzdálenosti x od kraje strany a I je proud, který stranou protéká.
Řešení
Řešení a)
Pro vyřešení této úlohy nám stačí určit, jakou silou je odpuzována jedna ze stran uvažovaného závitu. Celková síla působící na závit se dá složit ze sil, které působí na jednotlivé strany. Díky symetrii úlohy víme, že tyto síly budou pro každou ze stran stejné.
Vybereme si tedy jednu ze stran závitu a určíme, jakou silou \(\vec{F}\) ji odpuzuje druhý závit. Pro názornost si situaci nakreslíme.
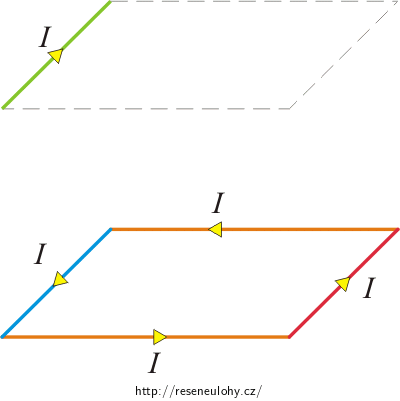
Vybraná strana prvního závitu má zelenou barvu. Ze skutečnosti, že navzájem kolmé vodiče na sebe navzájem silově nepůsobí, víme, že musíme určit, jakou silou na zelenou stranu budou působit modrá a červená strana druhého závitu. Protože se jedná o smyčku, bude jedna z těchto stran zelenou stranu odpuzovat a druhá přitahovat. Větší silou bude působit modrá strana, protože je zelené straně blíže. Závity se mají odpuzovat, proto musí modrá strana, která působí větší silou, zelenou stranu odpuzovat. Rovnoběžné vodiče se odpuzují, pokud jimi protéká proud opačným směrem. Z toho víme, že směr proudů ve smyčkách je opačný.
Řešení b)
Jde nám o to určit velikost síly, kterou se budou závity odpuzovat. Nejprve určíme velikost síly F1, kterou působí na zelenou stranu strana modrá. Situace je komplikovaná v tom, že magnetické pole není podél zelené strany homogenní. Musíme tedy nejprve určit závislost velikosti magnetické indukce B na vzdálenosti x bodu zelené úsečky od jejího kraje. Nakreslíme si obrázek.
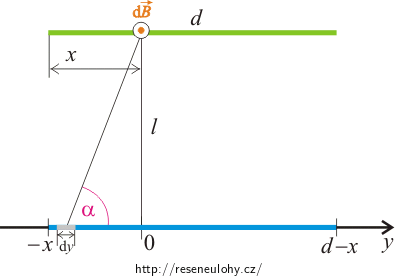
Odvození vztahu pro velikost celkové magnetické indukce v okolí úsečky s proudem nalezneme v oddíle úlohy Magnetické pole dlouhého přímého vodiče s proudem, Řešení 2:
\[ B(x)= \int_\mathrm{-x}^\mathrm{d-x}{\frac{\mu_0 I}{4\pi}\frac{l}{\left(l^2+y^2\right)^{\frac{3}{2}}}\,\mathrm dy}=\frac{\mu_0 I}{4 \pi } \left[\frac{y}{l\sqrt{y^{2}+l^{2}}}\right]_\mathrm{-x} ^\mathrm{d-x} = \frac{\mu_0 I}{4 \pi l} \left(\frac{d-x}{\sqrt{(d-x)^{2}+l^{2}}}+\frac{x}{\sqrt{x^{2}+l^{2}}}\right). \]Všechny příspěvky mají stejný směr. Na malý kousek délky dx zelené strany působí modrá strana silou dF = IB(x) dx, kde B(x) je velikost magnetické indukce v daném místě. Integrujeme přes délku zelené strany. Pro velikost síly F1 pak dostáváme
\[ F_1=\int_0 ^\mathrm{d} {B(x)} I \,\mathrm dx = \frac{\mu_0 I^{2}}{4 \pi l} \int_0 ^\mathrm{d}{\left(\frac{d-x}{\sqrt{(d-x)^{2}+l^{2}}}+\frac {x}{\sqrt{x^{2}+l^{2}}}\right)}\,\mathrm dx. \]Jedná se o součet v integrálu, proto můžeme integrál rozdělit na dva integrály a ty řešit samostatně (výsledek potom vynásobíme konstantou před závorkou). Dané integrály vyřešíme pomocí substituce:
\[\int_0^\mathrm{d}{\frac{d-x}{\sqrt{\left(d-x\right)^2+l^2}}\,\mathrm dx}=\]substituce:\(u=\left(d-x\right)^2+l^2\)\(\mathrm du= -2\left(d-x\right)\,\mathrm dx\)\[=-\frac{1}{2}\int_\mathrm{d^2+l^2}^\mathrm{l^2}{\frac{\mathrm du}{\sqrt{u}}}=-\frac{1}{2}\left[\frac{\sqrt{u}}{\frac{1}{2}}\right]_\mathrm{d^2+l^2}^\mathrm{l^2}=-l+\sqrt{d^2+l^2}.\]Teď spočítáme druhý integrál:
\[\int_0^\mathrm{d}{\frac{x}{\sqrt{x^2+l^2}}\,\mathrm dx}=\]substituce:\(z=x^2+l^2\)\(\mathrm dz=2x\,\mathrm dx\)\[=\frac{1}{2}\int_\mathrm{l^2}^\mathrm{d^2+l^2}{\frac{\mathrm dz}{\sqrt{z}}}=\frac{1}{2}\left[\frac{\sqrt{z}}{\frac{1}{2}}\right]_\mathrm{l^2}^\mathrm{d^2+l^2}=\sqrt{d^2+l^2}-l.\]Výsledky dosadíme a dopočítáme původní integrál:
\[F_1=\frac{\mu_0 I^2}{4\pi l}\left(-l+\sqrt{d^2+l^2}+\sqrt{d^2+l^2}-l\right)=\frac{\mu_0 I^2}{4\pi l}\cdot 2\cdot \left(\sqrt{d^2+l^2}-l\right) = \frac{\mu_0 I^{2}}{2\pi l}(\sqrt{l^{2}+d^{2}}-l). \]Tím jsme spočítali velikost síly, kterou na zelenou stranu působí modrá strana. Tato síla je kolmá k rovině závitu a směřuje nahoru.
Nyní se pustíme do určení velikosti síly F2, kterou na zelenou stranu působí červená strana. Výpočet je celou dobu analogický k prvnímu výpočtu. Pouze vzdálenost vodičů je tentokrát jiná.
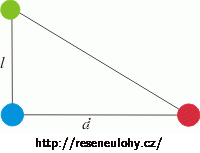
Barevné kruhy reprezentují strany, na závity se díváme ze strany. Tam, kde ve výpočtu F1 máme vzdálenost l, uvedeme teď \(\sqrt{l^2+d^2}\). Pro výsledný vztah velikosti síly F2 píšeme:
\[F_2=\frac{\mu_0 I^{2}}{2\pi \sqrt{l^2+d^2}} (\sqrt{l^2+2d^{2}}-\sqrt{l^2+d^2}).\]Červený vodič zelený přitahuje.
Máme určit velikost magnetické síly, kterou se závity odpuzují. K tomu potřebujeme složit síly, které na zelený vodič působí, a poté složit síly na všechny čtyři strany smyčky. Nakreslíme si obrázek působících magnetických sil.
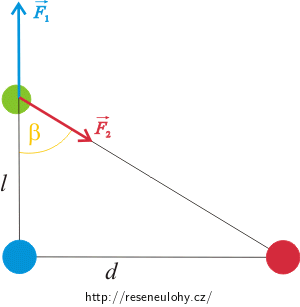
Závity se odpuzují, protože se vodorovné složky na jednotlivé strany vyruší. Pomocí obrázku určíme velikost svislé složky síly F, kterou působí druhý závit na zelenou stranu
\[F=F_1-F_2 \cos{\beta}.\]Velikost výsledné síly Fv, kterou se závity odpuzují, je čtyřnásobkem svislé složky síly F:
\[ F_\mathrm{v} = 4F = 4\left(F_1-F_2 \cos{\beta}\right)=\] \[=4\left[ \frac{\mu_0 I^{2}}{2\pi l}\cdot \left(\sqrt{l^{2}+d^{2}}-l\right)\right]-4\left[\frac{\mu_0 I^2}{2\pi \sqrt{l^2+d^2}}\cdot \left(\sqrt{l^2+2d^2}-\sqrt{l^2+d^2}\right)\cdot \frac{l}{\sqrt{l^2+d^2}}\right]=\] \[ =\frac{4\mu_0 I^2}{2\pi}\cdot\left[\frac{\sqrt{l^2+d^2}-l}{l}-\frac{l\left(\sqrt{l^2+2d^2}-\sqrt{l^2+d^2}\right)}{l^2+d^2}\right]=\] \[=\frac{2\mu_0 I^2}{\pi l}\cdot\left[\frac{\sqrt{l^2+d^2}-l}{l^2}-\frac{\sqrt{l^2+2d^2}-\sqrt{l^2+d^2}}{l^2+d^2}\right].\]Zápis a číselné dosazení
l = 3 cm = 0,03 m vzdálenost závitů d = 4 cm = 0,04 m velikost strany čtverce I = 3 A proud tekoucí závitem Fv = ? (N) výsledná síla působící na závit Z tabulek: μ0 = 4π·10-7 Hm-1 permeabilita vakua
Poznámka: Vzdálenosti do hranaté závorky můžeme dosazovat v centimetrech, protože ve výpočtu se vyskytují ve zlomku, což znamená, že jednotky se nakonec vykrátí.
\[F_\mathrm{v}=\frac{2\mu_0 I^2}{\pi l}\cdot\left[\frac{\sqrt{l^2+d^2}-l}{l^2}-\frac{\sqrt{l^2+2d^2}-\sqrt{l^2+d^2}}{l^2+d^2}\right]=\] \[=\frac{2{\cdot} 4\pi \cdot 10^{-7} \cdot 3^2}{\pi\cdot 0{,}03}\cdot\left[\frac{\sqrt{3^2+4^2}-3}{3^2}- \frac{\sqrt{3^2+2{\cdot} 4^2}-\sqrt{3^2+4^2}}{3^2+4^2}\right]\,\mathrm N\,\dot{=}\,40 {\cdot} 10^{-6}\,\mathrm N\,\dot{=}\,40\,\mathrm{\mu N}\]Odpověď
Proudy ve vodičích mají opačný směr.
Závity se odpuzují silou 40 μN.