Energie a výkon magnetického pole cívky
Úloha číslo: 65
Cívka o indukčnosti 2 H a odporu 10 Ω je náhle připojena ke zdroji bez vnitřního odporu s napětím 100 V. Určete okamžitý výkon, s nímž se za 0,1 s po připojení:
a) hromadí energie v magnetickém poli,
b) uvolňuje Joulovo teplo na cívce,
c) odebírá energie ze zdroje.
Nápověda
Jak se na průběhu proudu projeví zapojená cívka?
Určete časový průběh proudu v obvodu.
Rozbor a)
Okamžitý výkon, s nímž se po připojení hromadí energie v magnetické poli, vypočítáme jako derivaci energie cívky podle času.
Pro výpočet energie magnetického pole potřebujeme znát okamžitý proud procházející cívkou.
Kdyby v obvodu cívka nebyla, vzrostl by proud okamžitě po připojení napětí. Cívka však vytváří v obvodu indukované elektromotorické napětí. Podle Lenzova zákona toto napětí brání změně, která ho vyvolala, tedy brání růstu proudu. To znamená, že indukované napětí má opačnou polaritu než baterie a proud roste postupně. Později, v ustáleném stavu, kdy obvodem teče konstantní proud, se cívka chová již jako obyčejný vodič.
Pomocí 2. Kirchhoffova zákona sestavíme rovnici pro neznámý proud. Z této diferenciální rovnice vyjádříme proud v závislosti na čase, který dosadíme do rovnice pro energii magnetického pole.
Řešení a)
Okamžitý výkon, s nímž se po připojení hromadí energie v magnetickém poli, vypočítáme jako derivaci okamžité energie podle času:
\[P(t)=\frac{\mathrm{d}E(t)}{\mathrm{d}t}.\]Pro okamžitou energii magnetického pole platí vztah:
\[E(t)=\frac{1}{2}LI(t)^{2},\]kde L je indukčnost cívky a I proud, který jí prochází.
Časovou závislost proudu určíme z rovnice pro napětí sestavené pomocí 2. Kirchhoffova zákona. Začneme v bodě 1 a postupujeme podél obvodu ve směru otáčení hodinových ručiček. Pro vyznačený směr proudu zaznamenáváme při průchodu baterií nárůst potenciálu o +U. Na rezistoru dochází k úbytku napětí o hodnotu -IR. Bod 3 má vyšší potenciál než bod 1, protože při rostoucím proudu brání indukované napětí tomuto růstu, a proto má směr vyznačený na obrázku. Když tedy přecházíme podél cívky z bodu 3 do bodu 1, změní se potenciál o UL = -L dI / dt.
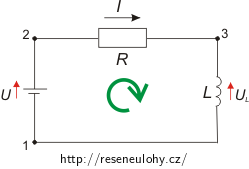
Smyčkové pravidlo tedy udává:
\[U-IR-L\frac{\mathrm{d}I}{\mathrm{d}t}=0,\]což je nehomogenní lineární diferenciální rovnice prvního řádu pro hledanou funkci I(t).
Rovnici si převedeme na tvar:
\[\frac{\mathrm{d}I}{\mathrm{d}t}+I\frac{R}{L}=\frac{U}{L}.\]Řešení nehomogenní diferenciální rovnice rozdělíme do tří kroků:
1. Vyřešíme homogenní diferenciální rovnici. To znamená, že pravá strana rovnice bude rovna nule:
\[L\frac{\mathrm{d}I}{\mathrm{d}t}+IR=0.\]Na jednu stranu rovnice převedeme neznámou v diferenciálním tvaru:
\[\frac{\mathrm{d}I}{dt}=-\frac{R}{L}I.\]Řešení homogenní diferenciální rovnice hledáme ve tvaru:
\[I_\mathrm{H} = Ce^\mathrm{\alpha t},\]kde C a α jsou konstanty.
Tento výraz dosadíme do homogenní diferenciální rovnice:
\[\frac{\mathrm{d}}{\mathrm{d}t}(Ce^\mathrm{\alpha t}) = -\frac{R}{L} C e^\mathrm{\alpha t},\] \[C e^{\alpha t} \alpha = -\frac{R}{L} C e ^{\alpha t}.\]Vyjádříme konstantu α:
\[\alpha = -\frac{R}{L}.\]Řešení homogenního diferenciálu je až na konstantu C určeno vztahem:
\[I_\mathrm{H} = Ce^{-\frac{R}{L}t}.\]2. Nalezneme alespoň jedno řešení nehomogenní diferenciální rovnice (tzv. partikulární řešení):
\[L\frac{\mathrm{d}I}{\mathrm{d}t}+IR=U.\]Řešení budeme hledat ve tvaru, který nebude závislý na čase. Po derivaci proudu IN podle času získáme tvar:
\[0+I_\mathrm{N} R =U,\] \[I_\mathrm{N}=\frac{U}{R}.\]3. Obecné řešení diferenciální rovnice se rovná součtu řešení homogenní a nehomogenní rovnice:
\[I =I_\mathrm{H} +I_\mathrm{N}=Ce^{-\frac{R}{L}t}+\frac{U}{R}.\]Konstantu C určíme z podmínky, že v čase t = 0 je proud I nulový:
\[0=Ce^{-\frac{R}{L}\cdot0}+\frac{U}{R}\] \[0=C+\frac{U}{R}\] \[C=-\frac{U}{R}.\]Řešení lineární diferenciální rovnice má tvar:
\[I = \frac{U}{R}\left(1-e^{-\frac{R}{L}t}\right).\]Po dosazení proudu I do rovnice pro energii magnetického pole E dostáváme:
\[E = \frac{1}{2}\,L\,\left(\frac{U}{R}\,\left(1-e^{-\frac{R}{L}t}\right)\right)^{2}.\]Okamžitý výkon, s nímž se v daný čas po připojení hromadí energie v magnetickém poli, vypočítáme jako derivaci energie podle času:
\[P_\mathrm{a}= \frac {\mathrm{d}}{\mathrm{d}t}\,\left(\frac{1}{2}\,L\,\frac{U^{2}}{R^{2}}\,\left(1-e^{-\frac{R}{L}t}\right)^{2}\right).\]Konstanty nezávisející na čase vytkneme před derivaci:
\[P_\mathrm{a}= \frac{1}{2}\,L\,\frac{U^{2}}{R^{2}}\,\frac {\mathrm{d}}{\mathrm{d}t}\left(1-e^{-\frac{R}{L}t}\right)^{2}.\]Funkce, kterou budeme derivovat je složená, proto budeme nejdříve derivovat vnější funkci a pak ji vynásobíme s derivací funkce vnitřní:
\[P_\mathrm{a}= \frac{1}{2}\,L\,\frac{U^{2}}{R^{2}}2 \left(1-e^{-\frac{R}{L}t}\right)\,(-e^{-\frac{R}{L}t})(-\frac{R}{L}).\]Po matematických úpravách dostáváme výraz pro velikost výkonu:
\[P_\mathrm{a}= \frac{U^{2}}{R}\,e^{-\frac{R}{L}t}\left(1-e^{-\frac{R}{L}t}\right).\]Rozbor b) a c)
Při přenesení náboje ve vnější části elektrického obvodu mezi dvěma místy, vykoná elektrické pole práci, která se rovná změně potenciální energie. Zákon zachování energie nám říká, že pokles elektrické potenciální energie musí být doprovázen přeměnou energie do jiné formy.
Reálnou cívku si můžeme představit jako rezistor a ideální cívku. Energie v cívce se bude hromadit v magnetickém poli. V rezistoru se energie bude přeměňovat na (Joulovo) teplo. Výkon P spojený s tímto přenosem se definuje jako rychlost přenosu energie za čas.
Pokud budeme chtít vyjádřit výkon, s nímž se uvolňuje Joulovo teplo, budeme uvažovat pouze energii na rezistoru. Naopak budeme-li chtít vyjádřit výkon, s nímž se odebírá energie ze zdroje, budeme brát v úvahu celou reálnou cívku.
Řešení b) a c)
Při přenesení náboje mezi místy, mezi kterými je napětí, vykoná elektrické pole a tedy i elektrický obvod práci, která se rovná změně potenciální energie:
\[\mathrm{d}E_\mathrm{p}=\mathrm{d}QU.\]Náboj dQ můžeme vyjádřit jako proud I krát malý čas dt:
\[\mathrm{d}E_\mathrm{p}=I\mathrm{d}tU.\]Výkon P definujeme jako rychlost přenosu energie za čas:
\[P=\frac{\mathrm{d}E_\mathrm{p}}{\mathrm{d}t}.\]Po zderivování potenciální energie dostáváme výraz:
\[P=UI.\]b) Reálnou cívku si můžeme představit jako rezistor a ideální cívku. Energie se bude přeměňovat v Joulovo teplo v rezistoru.
Pokud budeme chtít vyjádřit výkon, s nímž se uvolňuje Joulovo teplo, budeme uvažovat pouze rezistor. Tedy:
\[P_\mathrm{b}=U_\mathrm{R}I,\]kde UR je napětí na rezistoru, které si můžeme vyjádřit pomocí Ohmova zákona jako:
\[U_\mathrm{R}=RI.\]Po dosazení napětí rezistoru UR do rovnice pro výkon dostáváme:
\[P_\mathrm{b}=RI^{2},\]kam za proud I dosadíme proud procházející obvodem vyjádřený v části řešení a):
\[I = \frac{U}{R}\left(1-e^{-\frac{R}{L}t}\right).\]Okamžitý výkon, s nímž se po připojení uvolňuje Joulovo teplo na cívce, je:
\[P_\mathrm{b}=\frac{U^{2}}{R}\,\left(1-e^{-\frac{R}{L}t}\right)^{2}.\]c) Pokud chceme vyjádřit výkon, s nímž se odebírá energie ze zdroje, budeme brát v úvahu celou reálnou cívku. Pro tu platí
\[P_\mathrm{c}=U_\mathrm{c}I,\]kde napětí Uc je celkové napětí procházející obvodem.
Za proud I opět dosadíme celkový proud v obvodu vyjádřený v části řešení a).
Pro výkon, s nímž se po připojení odebírá energie ze zdroje, platí:
\[P_\mathrm{c}=\frac{U^{2}}{R}\,\left(1-e^{-\frac{R}{L}t}\right).\]Zápis a číselné dosazení
L = 2 H indukčnost cívky R = 10 Ω odpor cívky U = 10 V napětí zdroje t = 0,1 s doba připojení cívky ke zdroji Pa = ? (W) výkon, se kterým se hromadí energie v magnetické poli Pb = ? (W) výkon, se kterým se uvolňuje Joulovo teplo Pc = ? (W) výkon, se kterým se odebírá energie ze zdroje
\[P_\mathrm{a}=\frac{U^{2}}{R}\,e^{-\frac{R}{L}t}\left(1-e^{-\frac{R}{L}t}\right)=\frac{100^{2}}{10}\cdot\,e^{-\frac{10{\cdot}0{,}1}{2}}\left(1-e^{-\frac{10{\cdot}0{,}1}{2}}\right)\,\mathrm{W}=1000\cdot e^{-\frac{1}{2}}\,\left(1-e^{-\frac{1}{2}}\right)\,\mathrm{W}\,\dot{=}\,240\,\mathrm{W}\] \[P_\mathrm{b}=\frac{U^{2}}{R}\,\left(1-e^{-\frac{R}{L}t}\right)^{2}=\frac{10^{2}}{10}\,\left(1-e^{-\frac{10{\cdot}0{,}1}{2}}\right)^{2}\,\mathrm{W}\dot{=}150\,\mathrm{W}\] \[P_\mathrm{c}=\frac{U^{2}}{R}\,\left(1-e^{-\frac{R}{L}t}\right)=\frac{10^{2}}{10}\,\left(1-e^{-\frac{10{\cdot}0{,}1}{2}}\right)\,\mathrm{W}\,\dot{=}\,390\,\mathrm{W}\]Všiměte si, že výkon Pc, s nímž se odebírá energie ze zdroje, se rovná součtu výkonů Pa a Pb, s nimiž se hromadí energie v magnetickém poli a uvolňuje Joulovo teplo na cívce:
\[P_\mathrm{c}=P_\mathrm{b}+P_\mathrm{a}\]Odpověď
Okamžitý výkon, s nímž se po připojení zdroje hromadí energie v magnetickém poli, má velikost 240 W. Výkon, s nímž se po připojení uvolňuje Joulovo teplo, je 150 W. A výkon, s nímž se po zapnutí odebírá energie ze zdroje, má velikost 390 W.

