Sbírka řešených úloh

Nabitá úsečka 1

Úloha číslo: 274

• Nápověda: Označení veličin a obrázek

  Délku úsečky označíme písmenem l a vzdálenost konce nabité úsečky od bodu A písmenem d.

  Nyní zvolíme soustavu souřadnic a nakreslíme si obrázek. Počátek soustavy souřadnic zvolíme v bodě A.

  

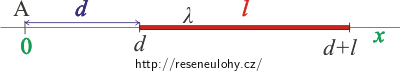
• Nápověda: Souvislost s bodovým nábojem

  Kladný bodový náboj Q vytváří ve vzdálenosti r elektrické pole o intenzitě

  \[E\,=\, \frac{1}{4 \pi \varepsilon_0}\, \frac{Q}{r^2}\,.\]

  Vektor intenzity míří od náboje.

  Zamyslete se nad tím, jak můžeme tohoto poznatku využít v této úloze.

• Řešení nápovědy

  Úsečku rozdělíme na malé kousky, které se budou chovat stejně jako bodové náboje.

  Celkovou intenzitu získáme „sečtením“ (přesněji zintegrováním) všech příspěvku od těchto malých kousků.

• Rozbor

  Nejprve zvolíme soustavu souřadnic. Celá úsečka bude ležet na ose x a bod A umístíme do počátku. V tomto případě bude vektor intenzity ležet také na ose x.

  Nabitou úsečku rozdělíme na malé části, které se budou chovat jako kladné bodové náboje. Celkovou intenzitu pak získáme zintegrováním příspěvků intenzit od jednotlivých kousků úsečky.

  Vektor intenzity má pro jednotlivé příspěvky vždy stejný směr, míří od úsečky ve směru osy x. Celková intenzita bude mít tedy také tento směr.

• Řešení

  Nejprve zvolíme soustavu souřadnic.

  Počátek zvolíme v bodě A. Nabitá úsečka bude ležet na ose x ve vzdálenosti d od bodu A (tzn. od počátku). Konce úsečky budou mít tedy souřadnice d a d + l.

  

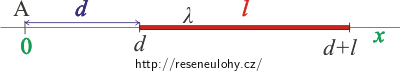
  Víme, že kladný bodový náboj o velikosti Q vytváří ve vzdálenosti r elektrické pole o intenzitě:

  \[E\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q}{r^2}\,.\]

  Vektor intenzity míří směrem od náboje.

  Rovnoměrně nabitou úsečku si tedy rozdělíme na malé části délky dx, které budou nabity nábojem dQ = λdx a které se budou chovat jako bodový náboj. λ je délková hustota náboje.

  

  Jeden takový kousek úsečky bude tedy v bodě A (který je ve vzdálenosti x) vytvářet elektrické pole s intenzitou o velikosti:

  \[\mathrm{d}E\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{\mathrm{d}Q}{r^2}\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{\lambda \mathrm{d}x}{x^2}\,.\tag{*}\]

  Vektor intenzity má pro jednotlivé příspěvky vždy stejný směr, míří od úsečky ve směru osy x. Celková intenzita bude mít tedy také tento směr.

  Celkovou intenzitu získáme integrací jednotlivých příspěvků přes celou délku úsečky:

  \[E\,=\int_\mathrm{d}^\mathrm{\small d+l} \mathrm{d}E.\]

  Za jednotlivé příspěvky dosadíme ze vzorce (*):

  \[E\,=\int_\mathrm{d}^\mathrm{\small d+l} \frac{1}{4 \pi \varepsilon_0}\, \frac{\lambda \mathrm{d}x}{x^2}\,.\]

  Konstanty vyjmeme před integrál:

  \[E\,=\,\frac{\lambda}{4 \pi \varepsilon_0}\int_\mathrm{d}^\mathrm{\small d+l} \frac{1}{x^2}\,\mathrm{d}x\]

  a určitý integrál vypočítáme:

  \[E\,=\,\frac{\lambda}{4 \pi \varepsilon_0}\,\left[ -\frac{1}{x}\right]_\mathrm{d}^\mathrm{\small d+l}\,=\,\frac{\lambda}{4 \pi \varepsilon_0}\,\left(-\,\frac{1}{d+l}\,+\, \frac{1}{d}\right). \]

  Výraz v závorce převedeme na společného jmenovatele:

  \[E\,=\,\frac{\lambda}{4 \pi \varepsilon_0}\,\frac{-d+d+l}{d \left( d+l\right)} \,=\,\frac{\lambda}{4 \pi \varepsilon_0}\,\frac{l}{d \left( d+l\right)}.\]

  Nyní zbývá už jen vyjádřit nábojovou hustotu λ pomocí celkového náboje Q a délky úsečky l

  \[\lambda\,=\,\frac{Q}{l}\]

  a dosadit do vzorce:

  \[E\,=\,\frac{Q}{4 \pi \varepsilon_0 l}\,\frac{l}{d \left( d+l\right)}\,=\,\frac{Q}{4 \pi \varepsilon_0 }\,\frac{1}{d \left( d+l\right)}\,.\]

  Získali jsme velikost intenzity elektrického pole ve vzdálenosti d od konce úsečky.

• Zápis a číselný výpočet

  Q = 0,2 nC = 2 · 10⁻¹⁰ C

  l = 60 cm = 0,6 m

  d = 10 cm = 0,1 m

  E = ? (V m⁻¹)

  Z tabulek:

  ε₀ = 8,85 · 10⁻¹² C² N⁻¹ m⁻²

  ---

  \[ \begin{eqnarray} E\,& =& \,\frac{Q}{4 \pi \varepsilon_0 }\,\frac{1}{d \left( d+l\right)}\,=\,\frac{2\cdot\,10^{-10}}{4 \pi 8{,}85{\cdot}10^{-12} }\,\frac{1}{0{,}1 \left( 0{,}1\,+\,0{,}6\right)}\,\mathrm{V\,m^{-1}}\\ E\,& \dot=& \,25{,}69\,\mathrm{V\,m^{-1}} \end{eqnarray}\]

• Odpověď

  Intenzita elektrického pole ve vzdálenosti d = 10 cm od konce nabité úsečky má velikost

  \[E\,=\,\frac{Q}{4 \pi \varepsilon_0 }\,\frac{1}{d \left( d+l\right)}\,\dot=\,25{,}69\,\mathrm{V\,m^{-1}}\,.\]

  Vektor elektrické intenzity míří od úsečky.

• Odkaz

  Velikost intenzity v místech mimo přímku, na které leží nabitá úsečka, je spočtena v úloze Nabitá úsečka 2.