Sbírka řešených úloh

Dva rovnoběžné vodiče s proudem

Úloha číslo: 53

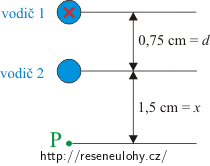
Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm jsou kolmé k rovině obrázku. Vodičem 1 protéká proud o velikosti 6,5 A směrem od nás. Jaký musí téci proud (velikost a směr) vodičem 2, aby výsledné magnetické pole v bodě P bylo nulové?

• Nápověda

  Uvědomte si, jaké magnetické pole vytváří přímý vodič s proudem.

  Jak musí být vzájemně orientovány magnetické indukce od obou vodičů, aby výsledné magnetické pole v bodě P bylo nulové?

• Rozbor

  Jelikož vodiči protéká elektrický proud, vytvářejí ve svém okolí magnetická pole. Magnetická indukce je největší u vodiče. Čím více se od něj vzdalujeme, tím je magnetická indukce menší.

  Magnetické pole znázorňujeme indukčními čarami, což jsou orientované čáry, jejichž tečny mají směr magnetické indukce B v daném bodě. Orientaci magnetické indukční čáry určíme severním pólem magnetky. V okolí vodiče s proudem mají indukční čáry tvar soustředných kružnic se středy v počátku. Orientace záleží na směru protékajícího proudu ve vodiči. Směřuje-li proud k nám (tedy před obrázek), mají křivky podle Ampérova pravidla pravé ruky směr proti směru hodinových ručiček a naopak.

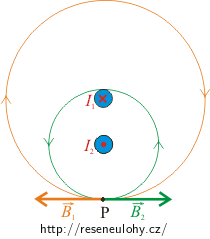
  V našem příkladě má být v bodě P magnetická indukce nulová. To znamená, že magnetická indukce od vodiče 1 musí být opačná než magnetická indukce od vodiče 2, a tedy proud ve vodiči 2 musí mít opačný směr než proud ve vodiči 1, tedy směrem k nám.

  Velikosti magnetických indukcí od obou vodičů se musí rovnat. Odtud určíme velikost proudu ve druhém vodiči.

   

  

• Řešení

  Jak již bylo uvedeno v rozboru, aby v daném bodě P byla celková magnetická indukce nulová, musí se velikosti magnetických indukcí od obou vodičů v daném bodě P rovnat a mít opačný směr. To znamená, že proud ve vodiči 2 poteče směrem k nám. Pro velikosti obou příspěvků platí:

  \[B_1=B_2.\]

  Velikost magnetické indukce ve vzdálenosti r od vodiče s proudem je dána vztahem

  \[B\,=\,\mu_\mathrm{0} \frac{I}{2\pi r},\]

  kde μ₀ je permeabilita vakua, I je proud protékající vodičem.

  Vzdálenost bodu P od vodiče 1 se rovná součtu \(r = d + x\):

  \[B_1= \mu_\mathrm{0}\frac{I_1}{2\pi(d+x)}.\]

  Vzdálenost bodu P od vodiče 2 je x:

  \[B_2=\mu_\mathrm{0}\frac{I_2}{2\pi x}.\]

  Velikosti magnetických indukcí B₁ a B₂ se mají rovnat:

  \[\mu_\mathrm{0}\frac{I_1}{2\pi(d+x)}=\mu_\mathrm{0}\frac{I_2}{2\pi x}.\] Vyjádříme neznámý proud I₂: \[I_2=\frac{I_1x}{d+x}.\]

• Zápis a číselné dosazení

  \(x\,=\,1{,}5\,\mathrm{cm}\)	vzdálenost bodu P od bližšího vodiče
  \(d\,=\,0{,}75\,\mathrm{cm}\)	vzdálenost vodičů
  \(I_1 \,=\,6{,}5\,\mathrm{A}\)	proud tekoucí prvním vodičem
  \(I_2\,=\,?\,\mathrm{(A)}\)	proud tekoucí druhým vodičem

  Není potřeba převádět vzdálenost z centimetrů na metry, jelikož rozměr délky máme v čitateli i jmenovateli zlomku a jednotka se tak „vykrátí“.

  ---

  \[I_2=\frac{I_1x}{d+x}=\frac{6{,}5\,\cdot\,1{,}5}{0{,}75+1{,}5}\,\mathrm{A}=4{,}3\,\mathrm{A}\]

• Odpověď

  Proud ve vodiči 2 má velikost

  \[I_2=4{,}3\,\mathrm{A}\]

  a opačný směr než proud ve vodiči 1, to znamená, že teče směrem k nám.