Přímý vodič v magnetickém poli
Úloha číslo: 2128
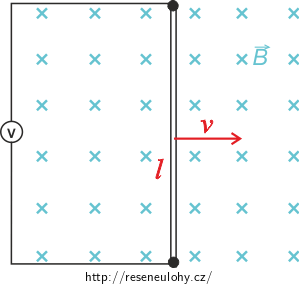
Přímý vodič délky 1 m se nachází v homogenním magnetickém poli o magnetické indukci 2 mT. Je umístěn kolmo k magnetickým indukčním čarám, jak ukazuje obrázek. Jakou rychlostí \(v\) se musí vodič pohybovat, aby indukované napětí mělo velikost 3 mV?
Nápověda
Ve vodiči se bude indukovat napětí. Vyhledejte si, jak zní Faradayův zákon elektromagnetické indukce a v něm použitý magnetický indukční tok.
O elektromagnetické indukci si můžete přečíst například zde: Elektromagnetická indukce
.
Rozbor
Podle Faradayova zákona se ve smyčce znázorněné na obrázku indukuje elektromotorické napětí, pokud se mění magnetický indukční tok plochou smyčky. Ten si můžeme představit jako „počet indukčních čar procházejících plochou smyčky“. Velmi důležité je si uvědomit, že nezáleží na celkovém počtu indukčních čar procházejících plochou smyčky, ale opravdu pouze na změně „jejich počtu“. Velikost elektromagnetického napětí a indukovaného proudu závisí na rychlosti změny „tohoto počtu“. Pohybuje-li se vodič stálou rychlostí doleva nebo doprava, zvětšuje se nebo zmenšuje obsah plochy smyčky, tedy i indukční tok smyčkou. V obvodu se bude v takovém případě indukovat napětí.
Řešení

Jak jsme si již v nápovědě řekli, zákon elektromagnetické indukce má tvar
\[U_\mathrm{i} = -\frac {\Delta \Phi}{\Delta t},\tag{1}\]kde \(\Phi\) je magnetický indukční tok, který je definován vztahem
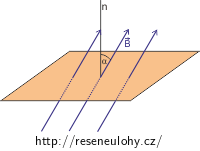
\[\Phi = B S \cos \alpha.\]Úhel \(\alpha\) je úhel, který svírá normála plochy \(S\) s vektorem magnetické indukce \(\vec{B}\). V našem případě je smyčka (její plocha) kolmá na vektor magnetické indukce a i během pohybu kolmá zůstává. Úhel, který svírá normála smyčky s vektorem magnetické indukce, je \(\alpha = 0^\circ.\) Můžeme tedy napsat
\[\Phi = B S.\tag{2}\]Pohybuje-li se vodič doprava nebo doleva rychlostí v, mění se plocha smyčky.
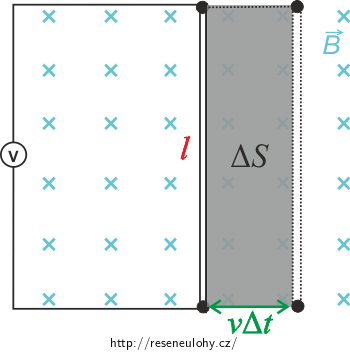
Za čas \(\Delta t\) se vodič posune o vzdálenost
\[\Delta s = v\Delta t\]a plocha se tedy změní o
\[\Delta S = lv\Delta t.\tag{3}\]Spojením (1), (2) a (3), dostaneme
\[U_\mathrm{i} = -\frac {B lv\Delta t }{\Delta t} = -{B lv}.\]Z rovnice vyjádříme rychlost v:
\[v = -\frac {U_\mathrm{i}}{B l}. \]Znaménko minus nám objasní Lenzův zákon, jenž hovoří o tom, že indukovaný proud v uzavřeném obvodu má takový směr, aby svým magnetickým polem působil proti změně indukčního toku, která je jeho příčinou.
Budou-li konce vodiče vodivě spojeny, aby vznikl elektrický obvod, bude obvodem procházet proud, jehož velikost bychom mohli dopočítat, pokud bychom znali celkový odpor obvodu.
Komentář – směr pohybu vodiče
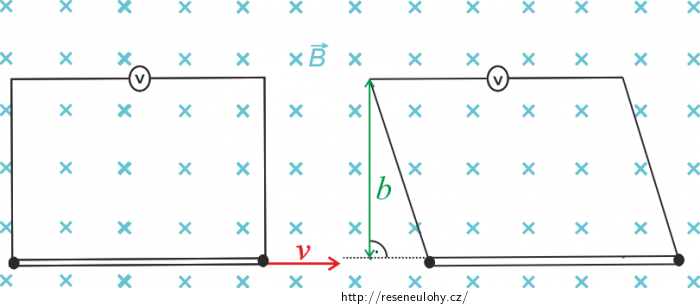
Zamysleme se nad případem, kdy je poloha vodiče taková, jak ukazuje následující obrázek.
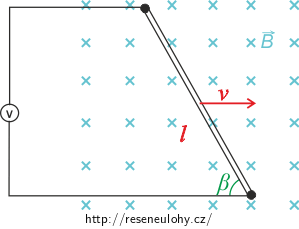
Stejně jako v případě ze zadání, mění se magnetický indukční tok. A stejně jako v předchozím případě použijeme Faradayův zákon magnetické indukce:
\[U_\mathrm{i} = - \frac {\Delta \Phi}{\Delta t}=-\frac {\Delta(BS\cos\alpha)}{\Delta t} = -\frac {\Delta(BS)}{\Delta t}.\]Stejně jako v předchozím případě je \(\cos \alpha = 1,\) jelikož normála plochy (smyčky) svírá s vektorem magnetické indukce \(0^\circ.\)
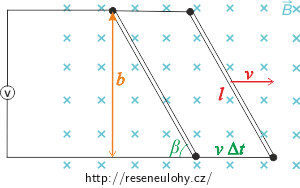
Pohybuje-li se vodič doprava nebo doleva rychlostí v, mění se plocha smyčky.
Za čas \(\Delta t\) se vodič posune o vzdálenost
\[\Delta s = v \Delta t.\]Když uvažujeme o tom, o kolik se změní plocha smyčky, je důležité si uvědomit, obsah jakého rovinného útvaru počítáme. Obrázek nám zcela správně ilustruje, že se jedná o rovnoběžník. Pro připomenutí — obsah rovnoběžníku se počítá podle vzorce \(S= a v_\mathrm{a}\), kde \(v_\mathrm{a}\) je výška strany a.
V našem výpočtu bude straně a odpovídat vzdálenost mezi dvěma naznačenými vodiči (v obrázku označeno jako \(v\Delta t\)), výšku na tuto stranu označíme b a dopočítáme pomocí goniometrických funkcí:
\[b = l \sin \beta,\] \[S = v\Delta t l \sin \beta.\]Vrátíme-li se k Faradayovu zákonu elektromagnetické indukce, dostaneme
\[U_\mathrm{i}=-\frac {Bl v\Delta t \sin \beta}{\Delta \ t} = - Bl v \sin \beta.\]Volíme-li \(\beta = 90^\circ\), pak se mění plocha smyčky a jedná se o případ, který jsme počítali původně. Po dosazení vyjde stejný výsledek jako v předchozím výpočtu, což nás utvrzuje ve správnosti výpočtu.
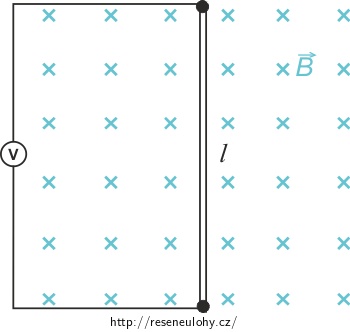
Pro \(\beta = 0^\circ\) naopak dostáváme nulové indukované napětí. I tento výsledek je zcela správný. Pokud je \(\beta = 0^\circ\), pak se vodič sice pohybuje kolmo k vektoru magnetické indukce, ale plocha smyčky zůstává stejná (viz obrázek).
Zápis a číselné dosazení
\(l = 1\,\mathrm{m}\) délka vodiče \(B=2\,\mathrm{mT}\) magnetická indukce pole \(U_\mathrm{i}=3\,\mathrm{mV}\) indukované napětí na vodiči \(v=\mathrm{?}\,\mathrm{m s^{-1}} \) rychlost pohybu vodiče
\[v = \frac {U_\mathrm{i}}{B l} = \frac {3{\cdot} 10^{-3}}{2{\cdot} 10^{-3} \cdot 1}\ \mathrm{m s}^{-1} = 1{,}5\ \mathrm{m s}^{-1}.\]Odpověď
Vodič se musí pohybovat rychlostí \(1{,}5\ \mathrm{m\ s^{-1}}\) .
Dynamický prvek
Následující aplet zobrazuje indukované napětí na přímém vodiči v magnetickém poli. Vodič je zobrazen zelenou úsečkou a indukované napětí se zobrazuje pouze tehdy, pokud se vodič pohybuje (animace je zapnutá).
Úlohy pro práci a apletem
- Nastavte hodnoty dle zadání a výsledku. Zkontrolujte, zda hodnota indukovaného napětí jim odpovídá.
- Nastavte všechny parametry na maximum, zapněte animaci a poznamenejte si indukované napětí. Poté nastavte úhel natočení na takovou hodnotu, aby indukované napětí bylo poloviční než v předchozím případě. Zdůvodněte, proč je to zrovna tento úhel?
- Zmáčkněte RESET, abyste aplet uvedli do základního nastavení. Spusťte animaci, poznamenejte si indukované napětí a poté animaci vypněte. Hodnotu magnetické indukce nyní nastavte na \(4 \space \mu \mathrm{T}\). Změnte libovolný jiný parametr tak, aby indukované napětí bylo stejné jako na začátku. Svoje řešení si ověřte spuštěním animace.