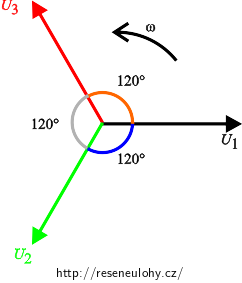
Spotřebič zapojený do trojúhelníka
Úloha číslo: 782
Symetrický spotřebič o impedanci jedné fáze Z = j50 Ω je zapojen do trojúhelníka podle obrázku a připojen na síť 230/400 V. Stanovte proudy I1, I2 a I3.
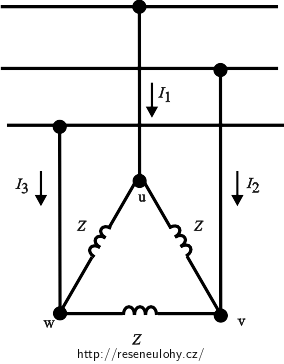
Zápis a značení
Z = j50 Ω hodnota impedance jedné fáze U = 230/400 V napětí sítě I1 = ? (A) fázový proud I2 = ? (A) fázový proud I3 = ? (A) fázový proud Obvykle se pro označení komplexních veličin používá označení s pruhem nad jejich značkou. Zde toto označení používat nebudeme, protože by vzorce byli méně přehledné. Všechny zde uvedené veličiny jsou brány komplexně, až na napětí sítě U.
Nápověda 1
Do obrázku ze zadání vyznačte jednotlivá fázová a sdružená napětí.
Nápověda 2
Zapojení spotřebiče ze zadání si můžeme představit jako zapojení tří jednoduchých spotřebičů a tří zdrojů. Jaké zákony se používají pro řešení obvodů stejnosměrného proudu, pokud je v obvodu zapojeno více zdrojů? Mohli bychom stejné zákony aplikovat i v tomto případě, kdy máme střídavý proud?
Nápověda 3
Odvoďte vztahy pro výpočet fázových napětí v obvodu pomocí symbolicko–komplexní metody.
Rozbor
Rovnice potřebné k nalezení velikosti proudů tekoucích spotřebičem sestavíme na základě obou Kirchhoffových zákonů. Abychom však tyto zákony mohli použít, nesmíme zapomenout, že musíme pracovat s komplexními amplitudami proudů a napětí.
V obvodu si vyznačíme jednotlivá fázová a sdružená napětí a vyjádříme si jejich komplexní amplitudy. Poté si zvolíme vhodné smyčky a uzly, sestavíme pro ně rovnice a vyřešíme je.
Stačí nám vypočítat jeden z proudů. Ostatní dva proudy získáme pomocí symetrie zapojení.
Řešení – proud I1
Úlohu vyřešíme pomocí Kirchoffových zákonů. Nejprve do obrázku ze zadání vyznačíme jednotlivá fázová a sdružená napětí:
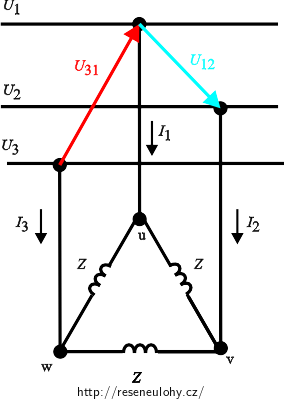
Zvolíme dvě smyčky:
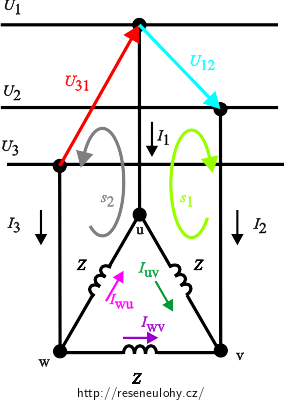
Aplikujeme Kirchhoffovy zákony: Druhý Kirchhoffův zákon pro smyčku s1 říká, že:
\[ -I_\mathrm{uv} \,Z + U_{12} = 0. \]Pro smyčku s2 platí:
\[ I_\mathrm{wu} \,Z - U_{31} = 0. \]Z prvního Kirchhoffova zákona pro uzel u lze vyjádřit rovnici:
\[ I_1 + I_\mathrm{wu} = I_\mathrm{uv}. \]
Získali jsme tři rovnice pro tři neznámé: Iuv, Iwu a I1. Tuto soustavu vyřešíme, resp. vyjádříme z ní hledaný proud I1:
\[ -I_\mathrm{uv} \,Z + U_{12} = 0, \tag{1}\] \[ I_\mathrm{wu} \,Z - U_{31} = 0, \tag{2}\] \[ I_1 + I_\mathrm{wu} = I_\mathrm{uv}. \tag{3}\]Z první a druhé rovnice vyjádříme proudy Iuv a Iwu a dosadíme do rovnice třetí:
\[ I_\mathrm{uv}=\frac{U_{12}}{Z}, \] \[ I_\mathrm{wu}= \frac{U_{31}}{Z}, \] \[ I_1 + \frac{U_{31}}{Z} = \frac{U_{12}}{Z}. \]Vyjádříme proud I1:
\[ I_1 = \frac{U_{12}-U_{31}}{Z}. \]Dosadíme za sdružená napětí U12 a U31 jejich vyjádření pomocí fázových napětí:
\[ I_1 = \frac{(U_1 - U_2)- (U_3 - U_1)}{Z}=\frac{2U_1 - U_2 - U_3}{Z}. \]Fázová napětí U1, U2 a U3 můžeme vyjádřit pomocí komplexní symboliky ve tvaru:
\[ U_1 = U,\] \[ U_2 = (-\frac{1}{2}-\mathrm{j}\frac{\sqrt{3}}{2})U,\] \[ U_3 = (-\frac{1}{2}+\mathrm{j}\frac{\sqrt{3}}{2})U.\]Dosadíme do vztahu pro proud I1:
\[ I_1 = \frac{2U_1 - U_2 - U_3}{Z} = \frac{2U - (-\frac{1}{2}-\mathrm{j}\frac{\sqrt{3}}{2})U - (-\frac{1}{2}+\mathrm{j}\frac{\sqrt{3}}{2})U}{Z} = \frac{(2+ \frac{1}{2}+ \mathrm{j}\frac{\sqrt{3}}{2} + \frac{1}{2} - \mathrm{j}\frac{\sqrt{3}}{2})U}{Z}= \frac{3U}{Z}.\]
\[ I_1 = \frac{3U}{Z}= \frac{3{\cdot} 230}{\mathrm{j}\,50}\,\dot=\, - \mathrm{j}\, 14\,\mathrm A \,\dot=\, 14\,\mathrm A. \]Řešení – proudy I2 a I3
Proudy I2 a I3 získáme díky poznatku, že zapojení spotřebiče je symetrické. Proudy tedy budou vůči sobě fázově posunuty, a to o 120°:
\[ I_1 = \frac{3U}{Z},\] \[ I_2 = \frac{3U}{Z}( -\frac{1}{2}-\mathrm{j}\frac{\sqrt{3}}{2}),\] \[ I_3 = \frac{3U}{Z} (-\frac{1}{2}+\mathrm{j}\frac{\sqrt{3}}{2}).\]
Odvození velikostí proudů I2 a I3 provedeme pomocí cyklické záměny indexů ve vztahu, ze kterého jsme odvodili proud I1 v předchozím oddíle. Tuto záměnu můžeme provést, protože zapojení spotřebiče je symetrické:
\[ I_1 = \frac{2U_1 - U_2 - U_3}{Z} = \frac{3U}{Z} \] \[ \Rightarrow I_2 = \frac{2U_2 - U_3 - U_1}{Z} ,\] \[ \Rightarrow I_3 = \frac{2U_3 - U_1 - U_2}{Z} .\]Do vztahů dosadíme výrazy pro sdružená napětí:
\[ U_3 = (-\frac{1}{2}+\mathrm{j}\frac{\sqrt{3}}{2})U,\] \[ U_2 = (-\frac{1}{2}-\mathrm{j}\frac{\sqrt{3}}{2})U.\] \[ U_1 = U.\]Dosadíme:
\[ I_2 = \frac{2U_2 - U_3 - U_1}{Z}= \frac{2[(-\frac{1}{2}-\mathrm{j}\frac{\sqrt{3}}{2})U] - [(-\frac{1}{2}+\mathrm{j}\frac{\sqrt{3}}{2})U] - U}{Z}= \frac{3U}{Z}(-\frac{1}{2}- \mathrm{j} \frac{\sqrt{3}}{2}),\] \[ I_3 = \frac{2U_3 - U_1 - U_2}{Z} = \frac{2[(-\frac{1}{2}+\mathrm{j}\frac{\sqrt{3}}{2})U] - U - [(-\frac{1}{2}-\mathrm{j}\frac{\sqrt{3}}{2})U]}{Z}= \frac{3U}{Z}(-\frac{1}{2}+ \mathrm{j} \frac{\sqrt{3}}{2}).\]Z obecného vyjádření velikostí proudů I1, I2 a I3 je možné vyčíst fázový posun mezi jednotlivými proudy, který je 120°. Symetrii zapojení a tedy i symetrii fázových proudů je možné ověřit také pomocí fázorového diagramu:
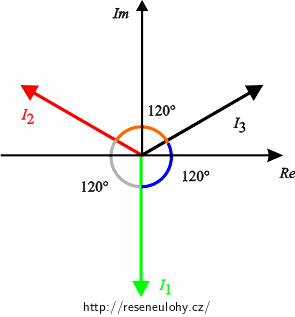
\[ I_2 = \frac{3U}{Z}( -\frac{1}{2}-\mathrm{j}\frac{\sqrt{3}}{2})= \frac{3{\cdot} 230}{\mathrm{j}\,50}( -\frac{1}{2}-\mathrm{j}\frac{\sqrt{3}}{2})\dot= (6{,}9 - \mathrm{j}\,12)\,\mathrm A. \] \[| I_2|\, \dot=\, 14 \,\mathrm A. \] \[ I_3 = \frac{3U}{Z} (-\frac{1}{2}+\mathrm{j}\frac{\sqrt{3}}{2})= \frac{3{\cdot} 230}{\mathrm{j}\,50} (-\frac{1}{2}+\mathrm{j}\frac{\sqrt{3}}{2})\dot= (6{,}9 + \mathrm{j}\,12)\,\mathrm A. \] \[| I_3|\,\dot=\, 14 \,\mathrm A. \]Odpověď
Velikosti hledaných proudů můžeme odvodit pomocí následujících rovnic:
\[ I_1 =\frac{2U_1 - U_2 - U_3}{Z} = \frac{3U}{Z},\] \[ I_2= \frac{2U_2 - U_3 - U_1}{Z} = \frac{3U}{Z}( -\frac{1}{2}-\mathrm{j}\frac{\sqrt{3}}{2}),\] \[ I_3 = \frac{2U_3 - U_1 - U_2}{Z} = \frac{3U}{Z} (-\frac{1}{2}+\mathrm{j}\frac{\sqrt{3}}{2}).\]A jejich číselné hodnoty jsou přibližně:
\[ |I_1| \,\dot=\, |I_2| \,\dot=\, |I_3| \,\dot=\, 14\,\mathrm A. \]