Bohrův model atomu vodíku
Úloha číslo: 324
Podle Bohrova modelu atomu vodíku se elektron pohybuje kolem jádra po kružnicové trajektorii o poloměru 52,9 pm se středem v jádru. Určete:
a) proud, který představuje pohybující se elektron,
b) magnetický moment, který je spojen s pohybem elektronu po této kružnici (tzv. orbitální magnetický moment elektronu),
c) určete velikost magnetické indukce pole buzeného pohybem elektronu ve středu atomu.
Nápověda
Při určování velikosti elektrického proudu, který představuje pohybující se elektron, vyjděte z definice pro elektrický proud: elektrický proud = náboj, který projde daným místem, dělený potřebným časem. Za časový interval můžete zvolit například periodu jednoho oběhu elektronu kolem nehybného jádra.
Pro výpočet velikosti magnetické indukce využijte Biotova-Savartova zákona.
Rozbor
Velikost elektrického proudu
V Bohrově modelu atomu vodíku elektron obíhá po kružnicové trajektorii kolem mnohem těžšího jádra. V rámci tohoto modelu obíhající elektron se záporným nábojem představuje malou proudovou smyčku. Na obrázku je znázorněn elektron obíhající určitou rychlostí kolem nehybného jádra.
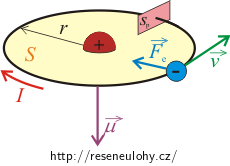
(Průměrný) elektrický proud určíme z toho, že náboj odpovídající náboji elektronu projde daným místem trajektorie jednou za periodu, tedy za čas jednoho oběhu elektronu kolem jádra. Abychom určili periodu oběhu elektronu kolem jádra, potřebujeme znát velikost rychlosti, s jakou se elektron pohybuje. Tu určíme z toho, že elektrická síla, která zakřivuje trajektorii elektronu, zde vystupuje jako síla dostředivá, má stejnou velikost i směr.
Určení orbitálního magnetického momentu
V Bohrově modelu vodíku obíhající elektron představuje malou proudovou smyčku, kterou můžeme charakterizovat magnetickým dipólovým momentem \(\vec{\mu}\). Směr magnetického dipólového momentu \(\vec{\mu}\) je dán pravidlem pravé ruky, kde zahnuté prsty ukazují směr proudu a vztyčený palec směr magnetického dipólového momentu. Velikost magnetického dipólového momentu závisí přímo úměrně na velikosti proudu, která smyčkou prochází, a na ploše smyčky.
Velikost magnetické indukce
Velikost magnetické indukce ve středu proudové smyčky určíme pomocí Biotova-Savartova zákona, viz úloha Magnetická indukce na ose kruhového závitu.
Řešení a) Velikost elektrického proudu
Velikost proudu I ve vodiči je definována jako množství náboje Q, které projde průřezem vodiče za čas Δt:
\[I=\frac{Q}{\,\mathrm{\Delta}t}.\]V našem případě obíhá kolem jádra vodíku pouze jeden elektron s nábojem o velikosti e. Pokud nás zajímá elektrický proud, který představuje tento obíhající elektron kolem jádra, budeme za časový úsek brát periodu T jednoho oběhu elektronu kolem jádra:
\[I=\frac{e}{T}.\]Pro určení periody T potřebujeme znát rychlost v, kterou elektron obíhá kolem jádra. Pro velikost rychlosti platí:
\[v=\frac{s}{T},\]kde s je délka trajektorie, kterou představuje kružnice o poloměru r. Můžeme psát, že
\[v=\frac{2\pi r}{T}.\]Pro periodu T platí:
\[T=\frac{2\pi r}{v}.\]Obíhající elektron vytvoří elektrický proud o velikosti:
\[I=\frac{ev}{2\pi r}.\tag{1}\]Velikost rychlosti v, se kterou se elektron pohybuje kolem atomového jádra, určíme z velikosti elektrické síly, která zakřivuje trajektorii elektronu, a působí tedy jako síla dostředivá:
\[F_\mathrm{e}=F_\mathrm{d}.\]Podle Coulombova zákona pro velikost elektrické síly platí:
\[F_\mathrm{e}=\frac{1}{4\pi \epsilon_\mathrm{0}}\frac{|Q_1||Q_2|}{l^2}.\]V našem případě jsou velikosti obou nábojů rovny náboji elektronu e a náboji protonu e. Veličina l značí vzdálenost mezi elektricky nabitými tělesy. V našem případě je rovna poloměru kružnice r, po které obíhá elektron atomové jádro. Dostáváme tedy:
\[F_\mathrm{e}=\frac{1}{4\pi \epsilon}\frac{e^2}{r^2}.\tag{2}\]Pro velikost dostředivé síly Fd, která působí na elektron, platí:
\[F_\mathrm{d}=\frac{m_\mathrm{e}v^2}{r}.\tag{3}\]Porovnáme vyjádření pro velikosti obou sil (2) a (3) a dostáváme vztah:
\[\frac{1}{4\pi \epsilon_0}\frac{e^2}{r^2}=\frac{m_\mathrm{e}v^2}{r},\]ze kterého vyjádříme velikost rychlosti v:
\[v^2=\frac{e^2}{4\pi \epsilon_0 m_\mathrm{e} r}\,\,\,\,\Rightarrow\,\,\,\,v=\frac{e}{\sqrt{4\pi \epsilon_0 m_\mathrm{e} r}}.\]Velikost rychlosti v dosadíme do vztahu (1) pro elektrický proud:
\[I=\frac{e^2}{4\sqrt{\pi^3r^3 \epsilon_0 m_\mathrm{e}}}.\]Získali jsme vyjádření pro velikost elektrického proudu, který vytvoří obíhající elektron kolem atomového jádra.
Řešení b) Určení orbitálního magnetického momentu
Magnetický moment, který je spojen s proudovou smyčkou tvořenou obíhajícím elektronem, se nazývá orbitální magnetický moment elektronu.
Směr magnetického dipólového momentu \(\vec{\mu}\) je dán pravidlem pravé ruky, kde zahnuté prsty ukazují směr proudu a vztyčený palec směr magnetického dipólového momentu \(\vec{\mu}\). Směr proudu je daný dohodou a je to směr kladně nabitých částic. Směr proudu je tedy opačný než směr obíhajícího elektronu kolem atomového jádra.
Výsledný směr magnetického momentu je znázorněn na obrázku.
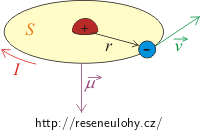
Pro velikost magnetického momentu proudové smyčky platí vztah:
\[\mu=IS,\tag{4}\]kde I je proud procházející smyčkou a S je obsah plochy rovinné smyčky.
Za velikost proudu dosadíme výraz vyjádřený v předchozím oddíle:
\[I=\frac{e^2}{4\sqrt{\pi^3r^3 \epsilon_0 m_\mathrm{e}}}.\]Obsah plochy smyčky S je roven obsahu kružnice s poloměrem r:
\[S=\pi r^2.\]Po dosazení těchto vztahů do rovnice (4) získáváme vztah pro velikost orbitálního magnetického momentu elektronu \(\mu\):
\[\mu=\frac{e^2}{4} \sqrt{\frac{r}{\pi \epsilon_0 m_\mathrm{e} }}.\]Řešení c) Velikost magnetické indukce
Pro velikost magnetické indukce B v libovolném bodě ležícím na ose závitu o poloměru r ve vzdálenosti x od středu smyčky platí podle úlohy Magnetická indukce na ose kruhového závitu :
\[B=\frac{\mu_0}{2}\, \frac{I r^2}{\left({r^2+x^2}\right)^{\frac{3}{2}}}.\]Pro velikost magnetické indukce Bs ve středu proudové smyčky dosadíme vzdálenost bodu P od středu smyčky x = 0:
\[B_\mathrm{s}=\frac{\mu_0}{2}\, \frac{I r^2}{\left({r^2+0}\right)^{\frac{3}{2}}},\] \[B_\mathrm{s}=\frac{\mu_0}{2}\, \frac{I }{r}.\] Pro velikost elektrického proudu I procházejícího smyčkou platí: \[I=\frac{e^2}{4\sqrt{\pi^3r^3 \epsilon_0 m_\mathrm{e}}}.\]Velikost magnetické indukce Bs ve středu proudové smyčky je dána vztahem:
\[B_\mathrm{s}=\frac{\mu_0}{8}\, \frac{e^2 }{\sqrt{\pi^3r^5 \epsilon_0 m_\mathrm{e}}}.\]Zápis a číselné dosazení
\(r=52{,}9\,\mathrm{pm}=52{,}9{\cdot} 10^{-12}\,\mathrm{m}\) poloměr kružnicové trajektorie \(I=?\,\mathrm{(A)}\) proud, který představuje pohybující se elektron \(\mu=?\,\mathrm{(Am^2)}\) orbitální magnetický moment elektronu \(B_\mathrm{s}=?\,\mathrm{(T)}\) velikost magnetické indukce pole buzeného pohybem elektronu ve středu atomu Z tabulek: \(m_\mathrm{e} \approx9{,}1 {\cdot} 10^{-31}\,\mathrm{kg}\) hmotnost elektronu \(e \approx1{,}6{\cdot} 10^{-19}\,\mathrm{C}\) elementární náboj \(\epsilon_0=8{,}85{\cdot} 10^{-12}\,\mathrm{F\cdot m^{-1}}\) permitivita vakua \(\mu_0 = 4 \pi\cdot 10^{-7}\,\mathrm{Hm^{-1}}\) permeabilita vakua
a)
\[I=\frac{e^2}{4\sqrt{\pi^3r^3 \epsilon_0 m_\mathrm{e}}}=\frac{\left( 1{,}6{\cdot} 10^{-19}\right)^2}{4\cdot\sqrt{\pi^3 \cdot(52{,}9{\cdot} 10^{-12})^3{\cdot} 8{,}85{\cdot} 10^{-12} \cdot 9{,}1 {\cdot} 10^{-31}}}\,\mathrm{A}\,\dot{=\,}1{,}1{\cdot} 10^{-3}\,\mathrm{A}=1{,}1\,\mathrm{mA}\]b)
\[\mu=\frac{e^2}{4}\, \sqrt{\frac{r}{\pi \epsilon_0 m_\mathrm{e} }}=\frac{\left(1{,}6{\cdot} 10^{-19}\right)^2}{4}\cdot{\sqrt{\frac{52{,}9{\cdot} 10^{-12}}{\pi \cdot 8{,}85{\cdot} 10^{-12} \cdot 9{,}1 {\cdot} 10^{-31} }}}\,\mathrm{Am^2}\,\dot{=}\,9{,}3{\cdot} 10^{-24}\,\mathrm{Am^2}\]c)
\[B_\mathrm{s}=\frac{\mu_0}{8}\, \frac{e^2}{\sqrt{\pi^3r^5 \epsilon_0 m_\mathrm{e}}}=\frac{4 \pi\cdot 10^{-7}}{8}\, \frac{\left( 1{,}6{\cdot} 10^{-19}\right)^2}{\sqrt{\pi^3\cdot(52{,}9{\cdot} 10^{-12})^5{\cdot} 8{,}85{\cdot} 10^{-12} \cdot 9{,}1 {\cdot} 10^{-31}}}\,\mathrm{T}\,\dot{=}\,12\,\mathrm{T}\]Odpověď
Pohybující se elektron představuje elektrický proud o velikosti přibližně:
\[I\dot{=}1{,}1\,\mathrm{mA}.\]Velikost orbitálního magnetického momentu spojeného s pohybem elektronu kolem jádra je přibližně:
\[\mu\dot{=}9{,}3{\cdot} 10^{-24}\,\mathrm{Am^2}.\]Magnetická indukce ve středu proudové smyčky má přibližně velikost:
\[B\dot{=}12\,\mathrm{T}.\]


