Netradiční obvody 3
Úloha číslo: 2153
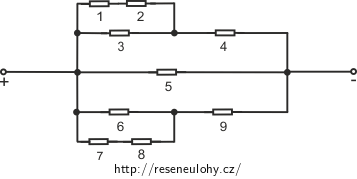
Určete celkový odpor zapojení na obrázku. Všechny rezistory mají stejný odpor R. Určete také napětí a proudy procházející jednotlivými rezistory.
Nápověda
Pokud si nejste jisti, jak se obvody s rezistory řeší, projděte si úlohu Řešení obvodu s rezistory.
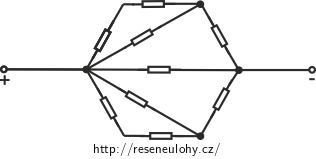
Klíčem k úspěchu je překreslit si celý obvod do „obvyklejšího tvaru“ tak, aby zapojení zůstalo stejné, ale bylo lépe vidět, který rezistor je s kterým zapojen paralelně, resp. sériově.
Pokud si s překreslením nevíte rady, pomůžou vám úlohy Netradiční obvody 1 a Netradiční obvody 2.
Dynamický prvek – překreslení obvodu
Následující aplet zobrazuje animaci překreslení obvodu.
Řešení – celkový odpor
Schéma rezistorů si překreslíme do obvyklejší formy a vyznačíme jednotlivé části, po kterých budeme obvod řešit.
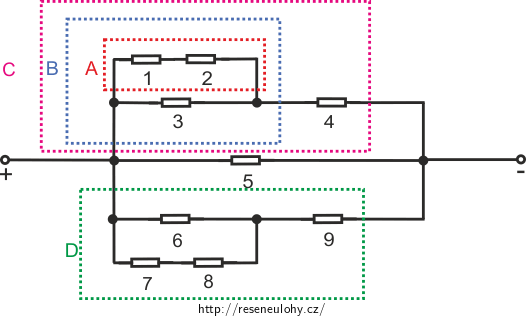
V této úloze volíme analogický postup jako v Spojování kondenzátorů I. Je-li tato úloha pro vás náročná, projděte si nejprve Spojování kondenzátorů I, kde je postup vysvětlen detailněji.
Nyní budeme skupiny rezistorů nahrazovat jedním rezistorem. Využijeme k tomu vztahy pro paralelní a sériové zapojení (viz Spojování kondenzátorů I, Řešení nápovědy – kapacita a Spojování kondenzátorů I, Řešení nápovědy – napětí a náboj). Využijeme také symetrii obvodu, abychom některé výpočty nemuseli provádět dvakrát. Všechny rezistory mají stejný odpor \(R\).
Rezistory 1 a 2 jsou zapojeny sériově:
\[R_\mathrm{A}=R + R=2R.\]Rezistory A a 3 jsou zapojeny paralelně:
\[\frac{1}{R_\mathrm{B}}=\frac {1}{R_\mathrm{A}} + \frac {1}{R}=\frac {1}{2R} + \frac {1}{R},\] \[{R_\mathrm{B}}=\frac {2}{3}R.\]Rezistory B a 4 jsou zapojeny sériově:
\[R_\mathrm{C} = R_\mathrm{B} + R=\frac{2}{3}R+R = \frac {5}{3} R. \]Díky symetrii obvodu můžeme vyjádřit odpor spodní části rezistorů D:
\[R_\mathrm{D} = R_\mathrm{C} = \frac {5}{3} R. \]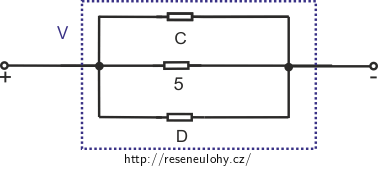
Rezistory C, D a 5 jsou zapojeny paralelně:
\[\frac {1}{R_\mathrm{V}} = \frac {1}{R_\mathrm{C}} + \frac {1} {R_\mathrm{D}} + \frac {1}{R}=\frac{1}{\frac{5}{3}R} + \frac{1}{\frac{5}{3}R} + \frac {1}{R} ,\] \[R_\mathrm{V}= \frac {5}{11} R.\]Výsledný odpor zapojení je \(R_\mathrm{V}= \frac {5}{11} R.\)
Nápověda – napětí a proud jednotlivými rezistory
Připomeňme si, co platí pro proud v sériovém a paralelním zapojení:
1. Při sériovém zapojení je celkový proud procházející obvodem roven proudům procházejícím jednotlivými spotřebiči. Napětí na rezistorech zapojených do série se sčítají.
2. Při paralelním zapojení platí, že součet proudů procházejících jednotlivými větvemi se rovná celkovému proudu. Napětí je na všech větvích stejné.
Díky těmto dvěma podmínkám si vyjádříme proudy procházející jednotlivými rezistory v obvodu v závislosti na celkovém proudu. Tentokrát budeme ale postupovat obráceně než v první části úlohy. Začneme od obvodu „s jediným rezistorem“ a budeme postupně „přidávat rezistory“, až dostaneme původní zapojení.
Řešení – napětí a proud
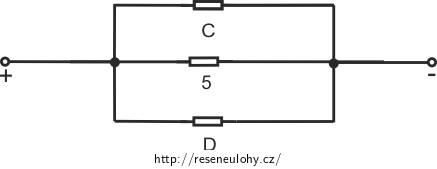
Nyní se vraťme k obvodu s rezistory C, D a 5, napětí na těchto rezistorech je stejné (viz nápověda) a je stejné jako napětí U na celém zapojení:
\[U_\mathrm{C} = U_\mathrm{D} = U_5 = U.\]Z předchozích výpočtů známe hodnoty odporů jednotlivých rezistorů:
\[R_\mathrm{C} = R_\mathrm{D}=\frac {5}{3}R \qquad R_5 = R.\]Proudy jednotlivými rezistory vyjádříme z Ohmova zákona \(R=\frac{U}{I}\):
\[I_\mathrm{C} = I_\mathrm{D} = \frac {3} {5} \frac {U}{R},\] \[ I_5 = \frac {U}{R}. \]Dále budeme úlohu řešit pouze pro horní část obvodu, ve spodní části obvodu budou díky symetrii zapojení stejné hodnoty.
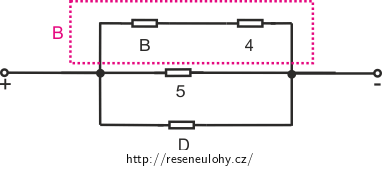
Rezistor C vzniknul nahrazením sériově zapojených rezistorů B a 4. Těmito rezistory musí procházet stejný proud jako nahrazujícím rezistorem C:
\[I_\mathrm{B} = I_4 = I_\mathrm{C} = \frac {3}{5} \frac {U}{R}.\]Napětí vyjádříme z Ohmova zákona \( U=RI\):
\[U_\mathrm{B}=R_\mathrm{B} I_\mathrm{B}=\frac {2}{3} R \frac{3}{5} \frac{U}{R}=\frac {2}{5}U, \] \[U_4=R_4 I_4 = R \frac{3}{5} \frac{U}{R}=\frac {3}{5}U. \]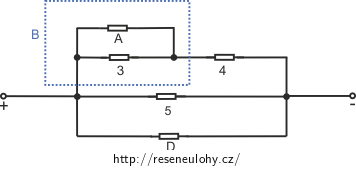
Rezistor B vzniknul nahrazením paraleleně zapojených rezistorů A a 3. Napětí na těchto rezistorech je tedy stejné a je stejné jako napětí na rezistoru B:
\[U_\mathrm{A}=U_3 = U_\mathrm{B}=\frac {2}{5}U.\]Proud vyjádříme z Ohmova zákona:
\[I_\mathrm{A} =\frac{U_\mathrm{A}}{R_\mathrm{A}} = \frac {\frac {2}{5}U}{2R} = \frac {1}{5}\frac {U}{R}, \] \[I_3 = \frac{U_3}{R_3} = \frac {\frac {2}{5}U}{R} =\frac {2}{5}\frac {U}{R}. \]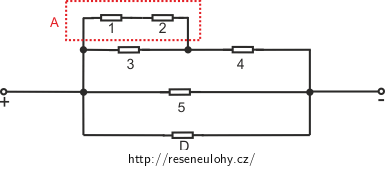
Rezistor A vzniknul nahrazením sériově zapojených rezistorů 1 a 2, tedy proud procházející těmito rezistory je stejný jako proud procházející rezistorem A:
\[I_1=I_2=I_\mathrm{A}=\frac {1}{5} \frac {U}{R}.\]Napětí vyjádříme z Ohmova zákona a zároveň využijeme toho, že se jedná o dva zcela identické rezistory:
\[U_1=U_2 =R I_1= R \frac {1}{5} \frac {U}{R} = \frac {1}{5} U. \]Jelikož je obvod souměrný (a rezistory mají stejný odpor), nemusíme již dopočítávat proudy a napětí na rezistorech 6, 7, 8 a 9. Hodnoty budou odpovídat hodnotám rezistorů souměrných podle osy. Tedy například napětí a proud na rezistoru 1 jsou stejné jako na rezistoru 7.
Odpověď
Celkový odpor zapojení \(R_\mathrm{V} = \frac {5} {11}R.\)
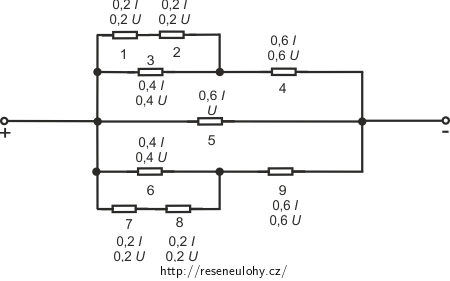
Proudy a napětí na jednotlivých rezistorech:
\[I_1 = I_7= \frac {1} {5} \frac {U}{R} \quad I_2=I_8 = \frac {1} {5}\frac {U}{R} \qquad I_3=I_6 =\frac{2}{5} \frac {U}{R} \qquad I_4=I_9 =\frac {3} {5} \frac {U}{R} \qquad I_5 = \frac {3}{5}\frac{U}{R} \] \[U_1=U_7= \frac {1} {5}U \qquad U_2=U_8 = \frac {1} {5}U \qquad U_3=U_6 = \frac {2}{5}U \qquad U_4=U_9 = \frac {3} {5} U \qquad U_5 = U. \]V následujícím schématu je použito označení \(I=\frac {U}{R}\), kde U je napětí na obvodu a R je odpor každého z rezistorů.