Odpor drátěné krychle

Úloha číslo: 37

Určete odpor drátěné krychle mezi různými dvojicemi vrcholů.

a) mezi vrcholy na tělesové úhlopříčce	b) mezi vrcholy na stěnové úhlopříčce	c) mezi vrcholy na jedné hraně

Odpor jedné hrany si označíme R.

Nápověda 1
Co se stane, když propojíte vrcholy se stejným potenciálem?

Které vrcholy mají stejný potenciál?
Řešení nápovědy 1
Mezi vrcholy se stejným potenciálem je nulové napětí. Tyto vrcholy tedy můžeme propojit (sloučit do jednoho uzlu), anižbychom tím změnili vlastnosti obvodu.

Vrcholy se stejným potenciálem najdeme díky symetrii jednotlivých obvodů.
Nápověda 2
Obvod si překreslete do roviny tak, že propojíte vrcholy se stejným potenciálem.
Rozbor
Napětí na rezistoru se rovná rozdílu potenciálů na obou svorkách spotřebiče (tj. „před“ a „za“ spotřebičem). Ve vrcholu A má potenciál nějakou danou hodnotu. V tomto bodě se náš obvod větví. Díky symetrii krychle víme, že některými větvemi (hranami vycházejícími z A) poteče stejný proud. To znamená, že na nich bude stejné napětí (mají stejný odpor), a tedy na koncích těchto hran bude stejný potenciál (potenciál v bodě A se změní o stejné napětí).

Vrcholy se stejným potenciálem můžeme sloučit do jednoho uzlu, protože by takovým spojovacím vodičem netekl žádný proud (stejný potenciál = nulové napětí). Touto úpravou obvodu nezměníme jeho vlastnosti, a tedy ani celkový odpor.

Najdeme si na krychli vrcholy se stejným potenciálem, které spojíme do jednoho uzlu. Zapojení si překreslíme do roviny a na každý drát doplníme rezistor o odporu hrany R.

Pomocí pravidel pro počítání odporů při sériovém a paralelním zapojení vypočítáme celkový odpor krychle.
Řešení části a) - odpor krychle mezi vrcholy H, B

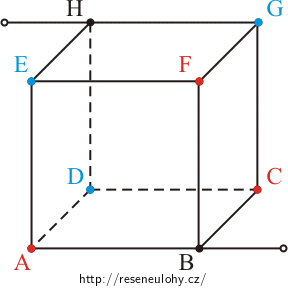
V tomto obvodu jsou hrany BA, BC a BF rovnocenné, protéká jimi stejný proud, a proto vrcholy A, C, F mají stejný potenciál. Propojením těchto bodů se celkový odpor krychle nezmění.

Stejně tomu je i u vrcholů D, E, G.

Vrcholy A, C, F, resp. D, E, G sloučíme do jednoho uzlu. Obvod si překreslíme do roviny a doplníme rezistory. Hodnota odporu každého rezistoru je R.

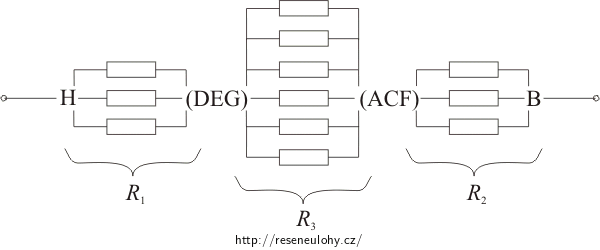
Odpor R₁ mezi uzly H, (DEG) a odpor R₂ mezi uzly (ACF), B se rovnají celkovému odporu tří paralelně zapojených rezistorů R:
\[\frac{1}{R_1}\,=\,\frac{1}{R_2}\,=\,\frac{1}{R}+\frac{1}{R}+\frac{1}{R}\] \[R_1\,=\,R_2\,=\,\frac{R}{3}.\]
Odpor R₃ mezi uzly (DEG), (ACF) je celkovým odporem šesti paralelně zapojených rezistorů R:
\[\frac{1}{R_3}\,=\,\frac{6}{R}\] \[R_3\,=\,\frac{R}{6}.\]
Odpory R₁, R₂ a R₃ jsou zapojeny sériově. Celkový odpor krychle mezi body H, B je tedy
\[R_\mathrm{HB}\,=\,R_1+R_2+R_3\,=\,2\frac{R}{3}+\frac{R}{6}\] \[R_\mathrm{HB}\,=\,\frac{5}{6}R\,.\]
Řešení části b) - odpor krychle mezi vrcholy E, B

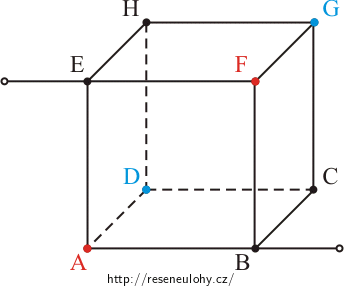
Při tomto zapojení jsou vrcholy A a F, resp. D a G rovnocenné a budou tedy mít stejný potenciál. Propojením těchto bodů celkový odpor krychle nezměníme.

Vrcholy A, F a vrcholy D, G spojíme do jednoho uzlu. Obvod si překreslíme a na obrázek doplníme rezistory o odporu R:

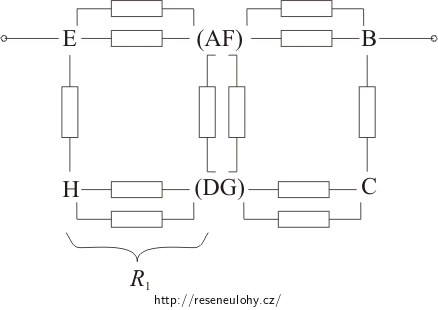
Všechny větve se dvěma paralelně zapojenými rezistory R nahradíme rezistory o odporu R₁, pro které platí:
\[\frac{1}{R_1}\,=\,\frac{1}{R}+\frac{1}{R}\] \[R_1\,=\,\frac{R}{2}\,.\]
Schéma obvodu si zjednodušíme:

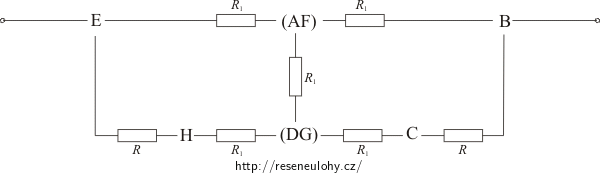
Rezistorem mezi body (AF) a (DG) díky symetrii obvodu nepoteče žádný proud. Uzly (AF) a (DG) mají stejný potenciál. Proto tento rezistor můžeme z obvodu úplně vynechat.

Pozn.: Podrobnější vysvětlení je uvedeno u úlohy Drátěný čtverec.

Sériově zapojené rezistory u vrcholů H a C nahradíme rezistory R₂:
\[R_2\,=\,R_1+R\,=\,\frac{R}{2}+R\,=\,\frac{3}{2}R\,.\]
Obvod si ještě jednou překreslíme:

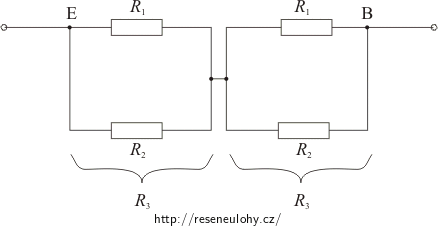
Nyní máme obvod se dvěma sériově spojenými rezistory R₃. Ty jsou tvořeny paralelně zapojenými rezistory R₁ a R₂.

Připomeňme, že \(R_1\,=\,\frac{R}{2}\), \(\hspace{10px} R_2\,=\,\frac{3}{2}R\).

Spočítejme odpor R₃:
\[\frac{1}{R_3}\,=\,\frac{1}{R_1}+\frac{1}{R_2}\,=\,\frac{R_1+R_2}{R_1R_2} \] \[\frac{1}{R_3}\,=\,\frac{\frac{R}{2}+\frac{3}{2}R}{\frac{R}{2}\cdot \frac{3}{2}R} \,=\,\frac{\frac{4}{2}R}{\frac{3}{4}R^2}\,=\,\frac{2}{\frac{3}{4}R}\,=\,\frac{8}{3R}\] \[R_3\,=\,\frac{3}{8}R\,.\]
Pro celkový odpor krychle tedy platí:
\[R_\mathrm{EB}\,=\,R_3+R_3\,=\,2R_3\,=\,2\frac{3}{8}R\] \[R_\mathrm{EB}\,=\,\frac{3}{4}R\,.\]
Řešení části c) - odpor krychle mezi vrcholy A, B

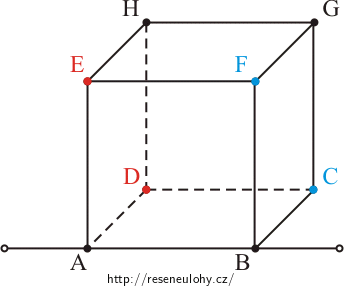
Vrcholy E, D a vrcholy F, C mají stejný potenciál. Propojením těchto bodů se celkový odpor krychle nezmění. Takže body E, D a body F, C spojíme do jednoho uzlu. Obvod si překreslíme do roviny a doplníme rezistory R:

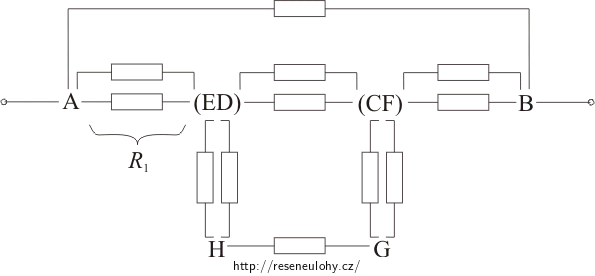
Větve se dvěma paralelně zapojenými rezistory R nahradíme odpory R₁, pro které platí:
\[\frac{1}{R_1}\,=\,\frac{1}{R}+\frac{1}{R}\] \[R_1\,=\,\frac{R}{2}\,.\]
Obvod si ještě jednou překreslíme:

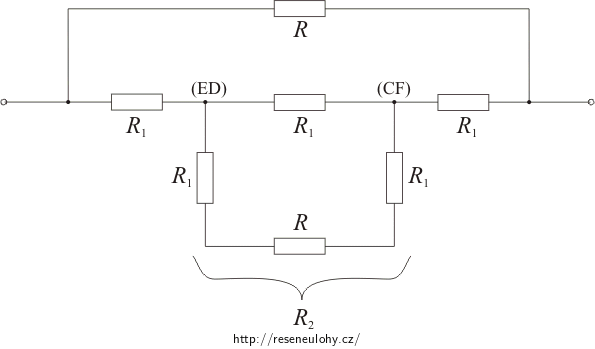
Pro odpor R₂ mezi uzly (ED) a (CF) platí:
\[\frac{1}{R_2}\,=\,\frac{1}{R_1}+\frac{1}{\left(R_1+R+R_1\right)}\] \[\frac{1}{R_2}\,=\,\frac{1}{\frac{R}{2}}+\frac{1}{2\frac{R}{2}+R}\,=\,\frac{2}{R}+\frac{1}{2R}\,=\,\frac{5}{2R}\] \[R_2\,=\,\frac{2}{5}R\,.\]
Pro celkový odpor krychle platí:
\[\frac{1}{R_\mathrm{AB}}\,=\,\frac{1}{R}+\frac{1}{R_1+R_2+R_1}\,.\]
Dosadíme \(R_1\,=\,\frac{R}{2}\), \(R_2\,=\,\frac{2}{5}R\) a vyjádříme R_AB
\[ \frac{1}{R_\mathrm{AB}}\,=\,\frac{1}{R}+\frac{1}{2\frac{R}{2}+\frac{2}{5}R}\,=\, \frac{1}{R}+\frac{1}{R+\frac{2}{5}R}\,=\,\frac{1}{R}+\frac{1}{\frac{7}{5}R} \] \[\frac{1}{R_\mathrm{AB}}\,=\,\frac{1}{R}+\frac{5}{7R}\,=\,\frac{12}{7R}\] \[R_\mathrm{AB}\,=\,\frac{7}{12}R\,.\]
Odpověď
Odpor drátěné krychle mezi vrcholy tělesové úhlopříčky je \(\frac{5}{6}R\).

Odpor drátěné krychle mezi vrcholy stěnové úhlopříčky je \(\frac{3}{4}R\).

Odpor drátěné krychle mezi vrcholy jedné hrany je \(\frac{7}{12}R\).
Odkaz na podobnou úlohu
Podobná úloha na řešení celkového odporu obvodu je úloha Drátěný čtverec. Tato úloha je řešena pomocí větví, kterými neteče žádný proud.