Vzájemná indukčnost cívek
Úloha číslo: 68
Dvě cívky mají vůči sobě pevnou polohu. Jestliže 1. cívkou proud neteče a proud 2. cívkou roste rychlostí 15,0 A/s, na 1. cívce vzniká elektromagnetické napětí 25,0 mV. Určete:
a) Jaká je vzájemná indukčnost cívek?
b) Když poteče 2. cívkou nulový proud a 1. cívkou proud 3,60 A, jaký je celkový magnetický tok 2. cívkou?
Nápověda 1
Vzájemná indukce je založena na následujícím jevu: Jestliže jednou z cívek prochází proměnný proud, vzniká v jejím okolí proměnné magnetické pole. Toto pole indukuje v druhé cívce napětí.
Nápověda 2
Když 1. cívkou neteče proud, je magnetický indukční tok procházející 1. cívkou přímo úměrný proudu v 2. cívce. Konstantu úměrnosti nazýváme vzájemná indukčnost a značíme ji M.
Rozbor
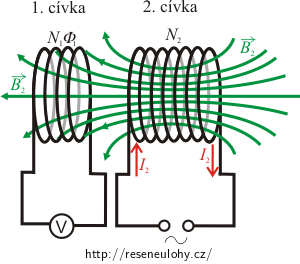
Obrázek ukazuje dvě cívky umístěné blízko sebe. Jestliže cívkou protéká elektrický proud, vytváří ve svém okolí magnetické pole. Měníme-li proud v jedné cívce, vzniká proměnné magnetické pole i v druhé cívce a indukuje se v ní elektromagnetické napětí dané Faradayovým zákonem. Mluvíme o vzájemné indukci, protože jde o vzájemné působení cívek, narozdíl od vlastní indukce, která se týká jedné cívky.
Podle zadání teče v 2. cívce proměnný proud. Tento proud vytváří proměnné magnetické pole, jehož okamžitá velikost je úměrná okamžité hodnotě proudu. Závity 1. cívky prochází magnetický indukční tok vyvolaný proudem 2. cívky. Magnetický indukční tok je úměrný velikosti magnetického pole. V cívce se indukuje elektromagnetické napětí, které můžeme změřit připojeným měřidlem.
Řešení a) Určení vzájemné indukčnosti
Jestliže se v 2. cívce mění proud, vzniká v jejím okolí proměnné magnetické pole, které prochází 1. cívkou a indukuje v ní elektromagnetické napětí. Magnetický indukční tok Φ1 procházející 1. cívkou je přímo úměrný proudu I2 v 2. cívce:
\[\Phi_{1} \sim I_2.\]Můžeme napsat:
\[\Phi_{1}=M I_2,\]kde konstanta úměrnosti M se nazývá vzájemná indukčnost 1. cívky vzhledem k 2. cívce.
Změníme-li vnějším zásahem proud I2, pak se změní i tok Φ1 (předchozí rovnici zderivujeme):
\[\frac{\mathrm{d} \Phi_{1}}{\mathrm{d}t} = M\frac{\mathrm{d}I_2}{\mathrm{d}t}.\]Levá strana této rovnice je podle Faradayova zákona rovna záporné hodnotě indukovaného napětí U1:
\[U_1=- \frac{\mathrm{d} \Phi_{1}}{\mathrm{d}t}=-M\frac{\mathrm{d}I_2}{\mathrm{d}t}.\]Ze vztahu vyjádříme vzájemnou indukčnost M:
\[\left|M\right|=\frac{U_1}{\frac{\mathrm{d}I_2}{\mathrm{d}t}}.\]Protože nás zajímá velikost vzájemné indukčnosti, bereme v úvahu absolutní hodnotu M.
Řešení b) Určení celkového magnetického indukčního toku 2. cívkou
Celkový magnetický tok procházející 2. cívkou si můžeme vyjádřit jako součet toků:
\[\Phi=\Phi_\mathrm{vl}+\Phi_\mathrm{vz},\]kde \(\Phi_\mathrm{vl}\) je magnetický tok 2. cívkou, který vznikne díky proudu, který prochází 2. cívkou. A platí pro něj:
\[\Phi_\mathrm{vl}=LI_2.\]Tok \(\Phi_\mathrm{vz}\) je tok, který bude 2. cívkou procházet díky přítomnosti 1. cívky s proudem. Jeho velikost je dána vztahem:
\[\Phi_\mathrm{vz}=MI_1.\]Konstanta úměrnosti M vyjadřuje vzájemnou indukčnost cívek. Má tedy stejnou hodnotu pro případ, kdy 1. cívkou prochází proud a ve 2. cívce se indukuje elektromotorické napětí, i pro případ, kdy 2. cívkou prochází proud a v 1. cívce se indukuje elektromotorické napětí.
Celkový magnetický tok procházející 2. cívkou je tedy:
\[\Phi=LI_2+MI_1.\]V naší úloze proud 2. cívkou neprochází, tedy se v ní nebude ani indukovat tok \(\Phi_\mathrm{vl}\). Výraz pro celkový tok se redukuje na tvar:
\[\Phi=MI_1.\]Za vzájemnou indukčnost cívek dosadíme vztah vyjádřený v předchozím oddíle Řešení a):
\[\left|M\right|=\frac{U_1}{\frac{\mathrm{d}I_2}{\mathrm{d}t}}.\]Výraz pro celkový magnetický tok procházející druhou cívkou je tedy dán vztahem:
\[\Phi=\frac{U_1I_1}{\frac{\mathrm{d}I_2}{\mathrm{d}t}}.\]Zápis a číselné dosazení
a)
\(I_1=0\,\mathrm{A}\) proud tekoucí první cívkou \(\frac{\mathrm{d}I_2}{\mathrm{d}t}=15\,\mathrm{As^{-1}}\) rychlost, kterou roste proud druhou cívkou \(U_1=25\,\mathrm{mV}\) napětí, které vzniká na první cívce \(M=\mathrm{?}\,\mathrm{(H)}\) vzájemná indukčnost cívek b)
\(I_1=3{,}6\,\mathrm{A}\) proud tekoucí první cívkou \(I_2=0\,\mathrm{A}\) proud tekoucí druhou cívou \(\Phi=\mathrm{?}\,\mathrm{(Wb)}\) celkový tok druhou cívkou
\[M=\frac{U_1}{\frac{\mathrm{d}I_2}{\mathrm{d}t}}=\frac{25{\cdot} 10^{-3}}{15}\,\mathrm{H} \,\dot{=}\, 1{,}67\,\mathrm{mH}\] \[\Phi=\frac{U_1I_1}{\frac{dI_2}{dt}}=\frac{25{\cdot} 10^{-3}\cdot3{,}6}{15}\,\mathrm{Wb}=6{\cdot} 10^{-3}\mathrm{Wb}=6{,}00\,\mathrm{mWb}\]Odpověď
Vzájemná indukčnost cívek má přibližně hodnotu \(1{,}67\,\mathrm{mH}.\)
Celkový magnetický tok 2. cívkou je \(6{,}00\,\mathrm{mWb}.\)