Sbírka řešených úloh

Použití Kirchhoffových zákonů pro řešení obvodu se dvěma zdroji

Úloha číslo: 21

Na obrázku je znázorněno zapojení se dvěma stejnými zdroji, které mají elektromotorické napětí 10 V, a dvěma stejnými rezistory, jejichž odpor je 20 Ω.

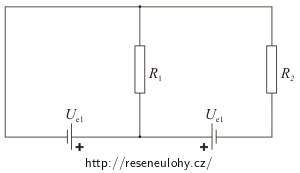
Určete proudy procházející jednotlivými rezistory. Vnitřní odpor zdrojů neuvažujte.

• Nápověda - znění Kirchhoffových zákonů

  Tento příklad budeme řešit pomocí Kirchhoffových zákonů. Uvědomte si, co tyto zákony říkají, nebo si je vyhledejte.

• Řešení nápovědy

  První Kirchhoffův zákon popisuje zákon zachování elektrického náboje. V každém bodě (uzlu) elektrického obvodu platí: Součet proudů vstupujících do uzlu se rovná součtu proudů z uzlu vystupujících.

  Druhý Kirchhoffův zákon formuluje pro elektrický obvod zákon zachování energie: Součet úbytků napětí na spotřebičích se v uzavřené části obvodu (smyčce) rovná součtu elektromotorických napětí zdrojů v této části obvodu (smyčce).

• Nápověda - „kuchařka“ pro použití Kirchhoffových zákonů

  

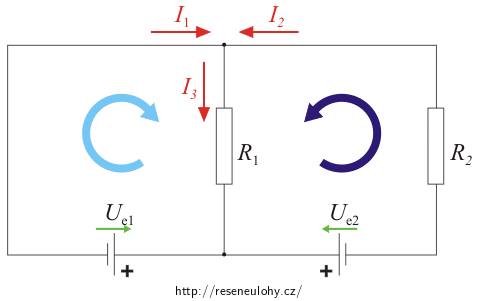
  1. Směr elektromotorického napětí zdroje si vyznačíme šipkou orientovanou ve směru působení neelektrostatických sil na kladnou částici, tedy „od - k +“ (v obrázku jsou tyto šipky znázorněny zelenou barvou).

  2. K uzlům sítě si nakreslíme směry proudů (červené šipky).

  3. Dále zvolíme uzavřené smyčky a jejich směr (modré šipky).

  Elektrická smyčka je uzavřená část obvodu, která se nerozdvojuje (tvoří cyklus).

  !!!POZOR!!! Volba směru proudů a smyček na začátku je libovolná, potom se však už musí dodržovat!

  4. Pomocí I. Kirchhoffova zákona napíšeme rovnice pro proudy v jednotlivých uzlech.

  5. Použijeme II. Kirchhoffův zákon a pro každou smyčku získáme další rovnici.

  Při psaní rovnic si musíme dávat pozor na znaménka. Jestliže má smyčka stejný směr jako proud, který prochází rezistorem (spotřebičem), pak úbytek napětí na rezistoru započítáme s kladným znaménkem. Pokud je smyčka orientovaná opačně než směr proudu, potom má úbytek napětí na rezistoru záporné znaménko. Je-li smyčka orientovaná stejně jako zdroj, pak má elektromotorické napětí zdroje kladné znaménko. Je-li smyčka orientovaná opačně, pak má elektromotorické napětí zdroje znaménko záporné.

  6. Z Kirchhoffových zákonů získáme rovnice (soustavu lineárních rovnic), jejichž řešením vyjádříme hledané hodnoty proudů.

  Pokud nám vyjde záporná hodnota proudu, znamená to, že jeho skutečný směr je opačný než směr, který jsme si zvolili na začátku.

• Řešení

  I. Kirchhoffův zákon: \[ I_1+I_2\,=\,I_3\,. \]

  II. Kirchhoffův zákon aplikujeme na smyčky (světle a tmavě modrá):

  \[ R_1I_3\,=\,-U_{e1} \tag{světlá}\] \[ R_2I_2+R_1I_3\,=\,-U_{e2} \tag{tmavá}\]

  Ze zadání příkladu víme, že \( R_1\,=\,R_2 \), \( \hspace{10px}U_{e1}\,=\,U_{e2} \). Odečteme-li tedy první rovnici od druhé, získáme vztah pro I₂:

  \[ R_2I_2\,=\,U_{e1}-U_{e2}\,=\,0\] \[I_2\,=\,0\,.\]

  Z prvního Kirchhoffova zákona nyní dostaneme \(I_3\,=\,I_1\).

  Z druhého Kirchhoffova zákona pro světle modrou smyčku si vyjádříme I₃:

  \[ R_1I_3\,=\,-U_{e1}\] \[I_3\,=\,-\,\frac{U_{e1}}{R_1}\,.\]

• Číselné dosazení

  Řešením Kirchhoffových zákonů jsme dostali rovnice pro proudy I₂, I₃:

  \[I_2\,=\,0\,\mathrm{A}\] \[I_3\,=\,-\frac{U_{e1}}{R_1}\,.\]

  Nyní dopočítáme hodnotu proudu I₃:

  \[I_3\,=\,-\frac{10}{20}\,\mathrm{A}\,=\,-0{,}5\,\mathrm{A}\,.\]

  Záporný výsledek znamená, že skutečný směr proudu I₃ je opačný než námi vyznačený směr v obrázku.

• Odpověď

  Rezistorem R₁ prochází proud 0,5 A, rezistorem R₂ proud 0 A.

• Odkaz na podobnou úlohu

  Zkuste také obtížnější úlohu na řešení Kirchhoffových zákonů: Využití Kirchhoffových zákonů pro výpočet celkového odporu zapojení