Sbírka řešených úloh

Napětí na voltmetru v RLC obvodu v rezonanci.

Úloha číslo: 778

V obvodu sestaveném podle schématu na obrázku je efektivní hodnota napětí 120 V a na kondenzátoru 160 V. Stanovte efektivní hodnotu napětí naměřenou na voltmetru V₂, jestliže je obvod v rezonanci.

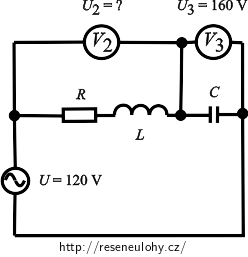
Pozn.: Všechny voltmetry považujte za ideální.

• Nápověda

  Uvědomte si, čemu se rovná celková impedance sériového RLC obvodu v případě rezonance.

  Jaké vztahy platí v takovém případě mezi napětími na jednotlivých prvcích a celkovým napětím?

• Řešení nápovědy

  Sériový RLC obvod je v rezonanci právě tehdy, když dojde k vyrovnání kapacitance kondenzátoru a induktance cívky. To také znamená, že celková impedance obvodu je rovna rezistanci rezistoru.

  V rezonanci je efektivní napětí na kondenzátoru a na cívce stejné. Napětí na obou prvcích jsou vždy v protifázi, a proto se díky stejné velikosti v rezonanci zcela odečtou. Efektivní napětí na zdroji se tedy rovná efektivnímu napětí na rezistoru.

• Rozbor

  Nakreslíme si fázorový diagram pro sériové zapojení RLC obvodu v rezonanci.

  Fázor napětí na rezistoru se rovná fázoru celkového napětí a fázor napětí na cívce je stejně dlouhý jako fázor napětí na kondenzátoru. Hledané napětí získáme součtem fázorů napětí na rezistoru a cívce.

• Řešení

  Z poznatku, že je sériový RLC obvod v rezonanci, vyplývá:

  \[ U_\mathrm{L} = U_\mathrm{C}, \]

  kde U_L je efektivní napětí na cívce a U_C efektivní napětí na kondenzátoru.

  Ze schématu zapojení obvodu v zadání vidíme, že:

  \[ U_\mathrm{C} = U_3, \]

  kde U₃ je napětí měřené na kondenzátoru voltmetrem V₃.

  Dále platí, že v rezonanci je celková impedance obvodu Z rovna velikosti rezistance (odporu) rezistoru R. Proto lze pomocí Ohmova zákona psát:

  \[ U = Z I = R I = U_\mathrm{R}, \] \[ U = U_\mathrm{R}, \]

  kde U_R je efektivní napětí na rezistoru a U je efektivní napětí dodávané zdrojem.

  Nakreslíme fázorový diagram:

  

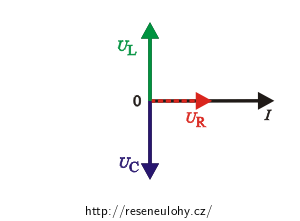
  Do fázorového diagramu si naznačíme rovnosti napětí popsané výše:

  

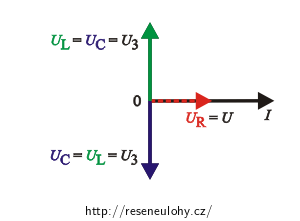
  Napětí na cívce a rezistoru U₂ získáme pomocí fázorového diagramu jako součet fázoru napětí na cívce U_L a fázoru napětí na rezistoru U_R.

  

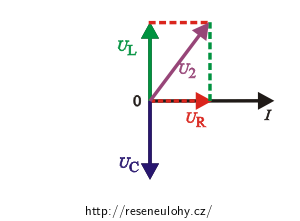
  Z fázorového diagramu plyne:

  \[ U_2 = \sqrt{U_\mathrm{R}^2 + {U_\mathrm{L}}^2} = \sqrt{U^2 + {U_3}^2}\ . \]

• Zápis a číselné dosazení

  U = 120 V	efektivní hodnota napětí zdroje
  U3 = 160 V	hodnota napětí na kondenzátoru
  U2 = ? (V)	hodnota napětí na cívce a rezistoru

  ---

  \[U_2=\sqrt{ U^2+{U_3}^2}=\sqrt{ 120^2+{160}^2}\,\mathrm V= 200 \,\mathrm V\]

• Odpověď

  Efektivní hodnota napětí na voltmetru V₂ je 200 V.