Sbírka řešených úloh

Toroid se vzduchovou mezerou

Úloha číslo: 248

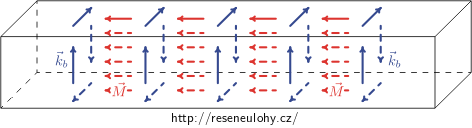
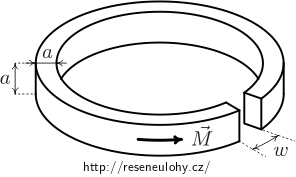
Ocelová tyč délky L a čtvercového průřezu o straně a byla homogenně zmagnetována (s magnetizací \(\vec M\) kolmou na průřez tyče) a poté ohnuta do tvaru toroidu s maličkou mezerou šířky w. Najděte magnetické pole v centru mezery; předpokládejte, že \(w \ll a\ll L\).

Návod: Představte si celou situaci jako superpozici celého toroidu a smyčky s opačnou orientací proudu, která bude simulovat mezeru.

• Nápověda 1

  Zatím ponechte tyč rovnou. Z magnetizace určete vázané proudy uvnitř a na povrchu tyče. V jaké elektrické součástce teče takový proud?

• Řešení nápovědy 1

  Magnetizaci tyče můžeme popsat pomocí objemového a plošného (vázaného) proudu — tyto dva proudy vytvářejí stejné magnetické pole jako zmagnetované těleso.

  Protože magnetizace je rovnoměrná (tj. vektor magnetizace \(\vec M\) je konstantní), libovolná parciální derivace podle libovolné souřadnice je nulová a tedy hustota objemového (vázaného) proudu \(\vec j_\mathrm{b}\) je též ve všech místech nulová, neboť pro ni platí

  \[\vec j_\mathrm{b} = \nabla\times\vec M.\]

  Pro hustotu povrchového (vázaného) proudu \(\vec k_\mathrm{b}\) platí

  \[\vec k_\mathrm{b} = \vec M\times\vec n_0,\]

  kde vektor \(\vec n_0\) je jednotkový vektor vnější normály k povrchu. Podle pravidla pravé ruky můžeme usoudit, že plošný proud jakoby obtéká tyč kolem dokola (rotuje kolem vektoru magnetizace). To je situace analogická hustě vinutému solenoidu.

  

  Na obrázku červené vektory vyjadřují vektor magnetizace, modré vektory znázorňují vektor hustoty plošného proudu.

• Nápověda 2

  Určete magnetické pole uvnitř zmagnetované tyče. Využijte faktu, že se chová jako solenoid, kterým na povrchu teče proud o plošné hustotě k_b.

• Řešení nápovědy 2

  Zmagnetovanou tyč si můžeme představit jako hustě vinutý solenoid s hustotou povrchového proudu o velikosti

  \[k_\mathrm{b} = |\vec M\times\vec n_0| = M.\]

  Pro magnetickou indukci pole uvnitř solenoidu pak platí

  \[B_1 = \frac{\mu_0NI}{l} = \mu_0k_\mathrm{b} = \mu_0M.\]

  Poznámka: Ve vztahu je správně μ₀, nikoliv μ. Ve chvíli, kdy nahrazujeme magnetizaci vázanými proudy, zároveň musíme materiál uvnitř tyče nahradit vakuem. Není to tak zvláštní, pokud si uvědomíme, že „materiál uvnitř tyče“ je vlastně přímo započítán do velikosti vázaných proudů. Ty totiž závisí na magnetizaci tyče.

• Nápověda 3

  Najděte pole ve středu čtvercového závitu jako superpozici polí čtyř drátů konečné délky.

  Pro velikost magnetické indukce pole drátu konečné délky, kterým teče proud I, platí vztah

  \[B = \frac{\mu_0I}{4\pi s}(\sin\,\theta_1-\sin\,\theta_2),\]

  kde s je kolmá vzdálenost daného místa od přímky drátu a θ_1,2 jsou úhly měřené od kolmice z daného místa k přímce drátu, pod kterými vidíme z daného místa konce drátu.

  

• Rozbor

  Využijeme možnosti nahradit magnetizaci tyče vázanými proudy, které budí stejné magnetické pole. Výpočet vázaných proudů — přesněji jejich plošné a objemové hustoty — můžeme provést přímo z magnetizace pomocí explicitních vztahů. Navíc, protože je magnetizace rovnoměrná, hustota objemového vázaného proudu bude nulová a plošná hustota v každém místě povrchu stejná.

  V takovém případě můžeme zmagnetovanou tyč nahradit solenoidem (uvnitř něhož je vakuum) s čtvercovým průřezem, jehož povrch obtéká plošný proud s výše vypočtenou hustotou. Jak spočítat magnetické pole uvnitř takového solenoidu, víme.

  Zde poznamenejme, že ohnutím tyče se nezmění její magnetizace, a tedy ani magnetické pole uvnitř ní.

  Magnetické pole v mezeře nyní vypočteme tak, že od pole uvnitř tyče odečteme pole, které vznikne „v jednom závitu“ (tj. mezeru si představíme jako „chybějící“ závit), tedy ve středu čtvercové smyčky. Proud v této smyčce odpovídá proudu, který teče po pásku solenoidu o šířce mezery. Pole ve středu čtvercové smyčky pak spočteme jako superpozici polí čtyř tenkých drátů konečné délky.

• Řešení

  Zmagnetování tyče můžeme nahradit vázanými proudy. Protože magnetizace je rovnoměrná (tj. vektor magnetizace \(\vec M\) je konstantní), libovolná parciální derivace podle libovolné souřadnice je nulová, a tedy objemové (vázané) proudy jsou nulové (viz Nápověda 1). Pro povrchový (vázaný) proud \(\vec k_\mathrm{b}\) platí

  \[\vec k_\mathrm{b} = \vec M\times\vec n_0,\]

  kde \(\vec n_0\) je jednotkový normálový vektor, z čehož vyplývá, že si zmagnetovanou tyč můžeme představit jako hustě vinutý solenoid s povrchovou hustotou proudu o velikosti k_b = M (viz nápověda 2).

  Pro magnetickou indukci pole uvnitř solenoidu pak platí

  \[B_1 = \frac{\mu_0NI}{l} = \mu_0k = \mu_0M\]

  Poznamenejme, že při výpočtu pole uvnitř solenoidu neuvažujeme materiál tyče, ale vakuum, což vyplývá z definice vázaných proudů, které „informaci o materiálu“ (přesněji jeho zmagnetování) obsahují. Proto ve vztahu vystupuje permeabilita vakua μ₀, nikoliv permeabilita daného materiálu μ.

  Máme najít magnetickou indukci v mezeře. Mezeru v tyči si představíme jako superpozici celého toroidu bez mezery a jednoho čtvercového závitu (o šířce w), ve kterém teče proud opačným směrem.

  Proto nyní spočítáme magnetickou indukci \(\vec B_2\) ve středu čtvercového závitu o straně a, kterým protéká proud o velikosti I = kw = Mw.

  Pole ve středu čtvercové proudové smyčky najdeme superpozicí polí čtyř drátů konečné délky. Uvažujeme-li drát konečné délky, pak magnetická indukce cirkuluje kolem drátu (stejně jako v nekonečném případě) a její velikost je

  \[B = \frac{\mu_0I}{4\pi s}(\sin\theta_1-\sin\theta_2),\]

  kde I je proud tekoucí drátem, s vzdálenost daného místa od přímky drátem určené a θ_1,2 úhly sevřené kolmicí z daného místa k přímce určené drátem a spojnicemi daného místa s konci drátu.

  

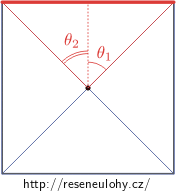
  V případě středu čtvercové smyčky jsou velikosti úhlů ±45° a vzdálenost s je rovna polovině straně čtverce, tj. s = a/2. Čtverec má čtyři strany, ze symetrie vyplývá, že všechny přispívají stejně velkou indukcí a příspěvky mají stejný směr a stejnou orientaci. Pro proud odpovídající mezeře o šířce w platí I = kw = Mw, takže

  \[B_2 = 4\,\cdot\, \frac{\mu_0I}{4\pi a/2}\left(\frac{\sqrt 2}{2}-\left(-\frac{\sqrt 2}{2}\right)\right) = \frac{2\sqrt 2\mu_0Mw}{\pi a}.\]

  Superpozicí pole toroidu a pole smyčky dostaneme velikost magnetické indukce v mezeře

  \[B = B_1-B_2 = \mu_0M\left(1-\frac{2\sqrt 2w}{\pi a}\right)\]

  a pro úzkou mezeru má směr magnetizace \(\vec M\).

• Odpověď

  Magnetické indukce v mezeře má velikost

  \[B = \mu_0M\left(1-\frac{2\sqrt 2w}{\pi a}\right)\]

  a má směr magnetizace \(\vec M\).

• Komentář – proč se ohnutím nepokazí pole

  Zbývá zodpovědět poslední otázku, kterou jsme se při řešení úlohy nezabývali: Proč se stočením tyče do toroidu nezmění uvnitř ní magnetické pole? Otázku rozdělíme na dvě části.

  Za prvé: Můžeme počítat uvnitř toroidu magnetické pole podle stejného vztahu jako u nekonečného solenoidu?

  Pro magnetickou indukci uvnitř hustě vinuté toroidální cívky skutečně platí obdobný vztah jako pro nekonečně dlouhý solenoid, a to \[B = \frac{\mu_0NI}{2\pi r},\] kde I je proud procházející solenoidem a r vzdálenost místa od centrální osy toroidu (přímky procházející středem toroidu). V případě, že pole určujeme ve středu průřezu, pak 2πr je vlastně délka tyče a vztah je formálně stejný jako u nekonečného solenoidu.

  Poznámka: Podrobný výpočet lze nalézt v úloze Magnetická indukce uvnitř toroidu, kde ale N označuje hustotu závitů, nikoli počet závitů.

  Za druhé: Nezmění se stočením tyče do toroidu její magnetizace? Přesněji, bude stále v každém průřezu tyče mít kolmý směr na jeho průřez?

  Jako určitý argument můžeme nabídnout, že jednou možnou definicí magnetizace je „hustota magnetických dipólů“ (přesněji hustota magnetického dipólového momentu) v materiálu. Tyto dipóly jsou pevně svázané s atomy (či molekulami) v mřížce, nebudou se tedy měnit prostým pohybem tyče.

  Pokud tedy uvnitř tyče jejím ohnutím nezpůsobíme nějaké drastické změny v atomové mřížce, potom není důvod, proč by se magnetické dipóly, pevně vázané na jednotlivé atomy v látce, měly přeorientovat. V jejich nejbližším okolí se ohnutí totiž prakticky neprojeví — pokud bychom uvažovali vliv okolních řádově tisíce až desetitisíce atomů, pak zde mluvíme o vzdálenostech řádově maximálně mikrometrů. Na této vzdálenosti tyč zůstává prakticky rovná.