Sbírka řešených úloh

Osm nábojů ve vrcholech osmiúhelníku

Úloha číslo: 267

• Poznámka: Znaménka nábojů

  Aby byly obrázky v řešení přehledné, náboje Q si zvolíme záporné (zakreslené modře) a náboj q kladný (zakreslený červeně). Pokud bychom znaménka nábojů zvolili jinak, bude postup řešení stejný, pouze se může změnit směr působících sil.

• a) Nápověda

  Nakreslete si obrázek sil, které působí na náboj q.

  1. způsob řešení:

  Využijte toho, že nábojů Q je sudý počet. Jaká je výsledná síla, kterou působí náboje Q umístěné v protilehlých vrcholech?

  2. způsob řešení:

  Zkuste vektory sil sečíst graficky.

• a) Řešení s využitím symetrie

  Síla, kterou působí každý náboj Q na náboj q, závisí na velikosti obou nábojů a na jejich vzájemné vzdálenosti. Protože mají všechny náboje Q stejnou velikost a zároveň jsou všechny stejně daleko od náboje q, působí na náboj q stejně velkými silami. Liší se pouze směry (viz obrázek).

  

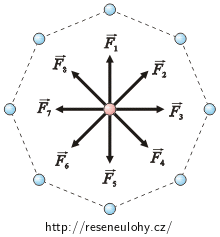
  Na obrázku vidíme, že náboje, které jsou v protilehlých vrcholech, působí na náboj q silami opačného směru. Protože mají tyto síly stejnou velikost, je jejich výslednice rovna nule. Tuto úvahu můžeme provést se všemi protilehlými dvojicemi nábojů. Výsledná síla, která působí na náboj q, je tedy rovna nule.

• a) Řešení: Obecnější postup

  Všechny náboje ve vrcholech osmiúhelníka mají stejnou velikost a od náboje q jsou stejně vzdálené. Síly, kterými jednotlivé náboje působí na náboj ve středu osmiúhelníka, jsou tedy stejně velké. Síly si zakreslíme do obrázku.

  

  Nyní vektory geometricky sečteme. Jeden ze způsobu je poskládat jeden vektor za druhý tak, aby každý vektor měl začátek tam, kde předchozí má konec. Výslednou sílu získáme, pokud spojíme počátek prvního vektoru s koncem posledního.

  Všechny vektory tedy postupně poskládáme za sebe. Začneme například vektorem označeným na obrázku jako \(\vec{F}_1\) a postupně po směru hodinových ručiček bereme další vektory.

  

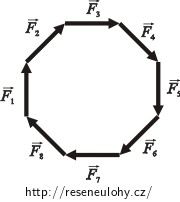
  Jak vidíme na obrázku, všechny vektory nám vytvoří pravidelný osmiúhelník. Umístíme-li poslední vektor, dostaneme se zpět do počátečního bodu. Výslednice sil, které působí na náboj q, je tedy rovna nule.

• b) Nápověda

  1. způsob řešení:

  Opět si nakreslete obrázek. Postupujte podobně jako v řešení časti a).

  Jak je to s výslednou silou, když v protilehlém vrcholu jednoho náboje je prázdné místo?

  2. způsob řešení:

  K řešení využijte předchozího výsledku: Síla, kterou působí osm nábojů na náboj ve středu, je rovna nule.

  Zkuste vymyslet, jaký náboj a kam musíme přidat, aby výsledná situace byla stejná, jak když jeden náboj odebereme.

• b) Řešení s využitím symetrie

  Budeme postupovat podobně jako v řešení části a). Náboje, které jsou v protilehlých vrcholech, působí na náboj q stejně velkými silami opačného směru. Oba vektory sil se tedy odečtou. Tuto úvahu můžeme provést se všemi náboji kromě jednoho, který v protilehlém vrcholu žádný náboj nemá (viz obrázek vlevo).

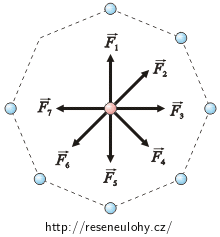
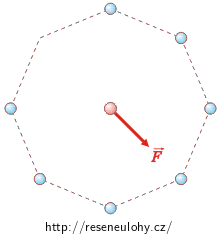
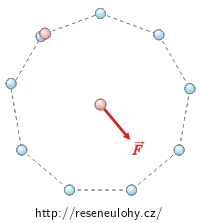
  Výsledná síla působící na náboj q se tedy rovná síle, která je způsobena nábojem Q, jenž má naproti sobě prázdné místo (viz obrázek vpravo). Její velikost spočítáme z Coulombova zákona:

  \[F\,=\, \frac{1}{4 \pi \varepsilon_0} \frac{Qq}{r^2}\,,\]

  kde r je vzdálenost nábojů.

• b) Řešení pomocí malého triku

  Abychom mohli při řešení využít výsledku z předchozího oddílu, použijeme menší trik a zadání úlohy trochu pozměníme. Víme, že pokud je v každém vrcholu osmiúhelníku jeden náboj Q, pak výslednice sil, které působí na náboj q, je rovna nule. Nyní bychom měli jeden náboj Q odebrat. Situace ale bude úplně stejná, pokud do jednoho vrcholu přidáme stejně velký náboj opačného znaménka. Na obrázku vlevo je vidět, že se vektory \(\vec{F}_8\) a \(\vec{F}_9\) odečtou.

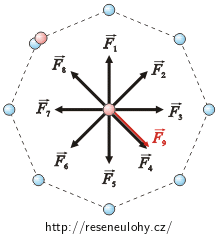
  V jednom z osmi vrcholů jsou tedy nyní dva náboje, které jsou stejně velké, ale mají opačné znaménko. Působení těchto nábojů na náboj q se vzájemně vyruší, a proto je situace stejná, jako by v tomto vrcholu nebyl náboj žádný.

  Nyní se můžeme pustit do výpočtu výsledné síly, která působí na náboj q.

  Výslednice sil, kterými působí osm stejných záporných nábojů, je rovna nule (viz část a). Celková síla, která tedy působí na náboj q, je rovna síle, kterou na něj působí kladný náboj Q. Velikost této síly spočítáme z Coulombova zákona:

  \[F_\mathrm{e}\,=\, \frac{1}{4 \pi \varepsilon_0} \frac{Qq}{r^2}\,,\]

  kde r je vzdálenost nábojů.

• c) Nápověda

  Tuto část úlohy řešte podobným postupem jako osmiúhelník. Tentokrát ale nemůžeme využít symetrie jako u osmiúhelníku, ale musíme použít skládání vektorů a malý trik s přidáním opačného náboje.

• c) Řešení

  Postup řešení bude stejný jako v případě osmi nábojů. Jediný rozdíl je v tom, že zde nemůžeme využít symetrie. Úlohu lze tedy řešit pouze jedním způsobem.

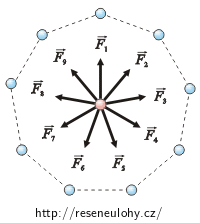
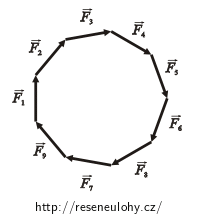
  Všechny náboje Q mají stejnou velikost a jsou od náboje q ve stejné vzdálenosti. Síly, kterými působí na náboj q, jsou tedy stejně velké. Výslednici sil získáme vektorovým součtem. Pokud naskládáme jeden vektor za druhý, vytvoří nám pravidelný devítiúhelník. Výsledná síla je tedy rovna nule.

  Místo abychom jeden náboj odebrali, můžeme do jednoho vrcholu přidat stejně velký náboj, ale s opačným znaménkem. Síly, kterými působí devět stejných nábojů, se navzájem ruší. Výslednice je tedy rovna síle, kterou na náboj q působí kladný náboj Q.

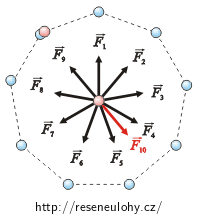
  Její velikost vypočítáme z Coulombova zákona:

  \[F\,=\, \frac{1}{4 \pi \varepsilon_0} \frac{Qq}{r^2}\,.\]

• Odpověď

  Výsledná síla, která působí na náboj q uprostřed osmiúhelníka i devítiúhelníka, je rovna nule.

  Pokud jeden náboj z vrcholu osmiúhelníka nebo devítiúhelníka odebereme, bude na náboj q působit síla o velikosti:

  \[F\,=\, \frac{1}{4 \pi \varepsilon_0} \frac{Qq}{r^2}\,.\]

• Jak by to bylo pro pravidelný n-úhelník

  Všimněte si, že postup řešení u devítiúhelníku byl stejný jako pro osmiúhelník. Pokud bychom měli jakýkoliv pravidelný n-úhelník, budeme opět postupovat úplně stejně.

  Je-li v každém vrcholu jeden náboj, je výslednice sil působících na náboj ve středu rovna nule. Chybí-li jeden náboj, je výsledná síla stejná jako síla, kterou by působil náboj opačného znaménka umístěný v jednom z vrcholů.

  Pokud je navíc n sudé, můžeme využít symetrie a vyřešit úlohu stejně jako v případě osmiúhelníka.

• Dynamický prvek

  Následující aplet zobrazuje n-úhelník se stejně velkými zápornými náboji ve vrcholech. Uprostřed n-úhelníku je kladný náboj. Aplet zobrazuje síly na kladný náboj uprostřed — od jednotlivých záporných nábojů jsou nakresleny černě, jejich výslednice potom červeně (je-li nulová, naznačuje to červený bod uprostřed n-úhelníku).

  Dále je možné odstranit náboj z jednoho vrcholu.

  Úkoly, které pomohou při řešení zadané úlohy (pokud již máte úlohu vyřešenou, můžete aplet využít ke kontrole řešení a rozšíření řešení na další pravidelné n-úhelníky):

  Úlohy pro práci s apletem

  1. Nastavte počet vrcholů na 4, vypněte zobrazování výslednice a odstraňte náboj z jednoho vrcholu. Rozmyslete si, kam bude mířit výslednice. Správnost ověřte pomocí apletu (zapněte zobrazování výslednice). Vyzkoušejte i pro další sudé počty vrcholů.
  2. Nastavte počet vrcholů na 3, vypněte zobrazování výslednice a odstraňte náboj z jednoho vrcholu. Rozmyslete si, kam bude mířit výslednice. Správnost ověřte pomocí apletu (zapněte zobrazování výslednice). Vyzkoušejte i pro další liché počty vrcholů.
  3. V obou případech porovnejte výslednici sil se silou, kterou by na náboj uprostřed působil náboj, který jsme odebrali. Dalo by se toho nějak využít při řešení úlohy?
  4. Na základě předchozích otázek rozmyslete, jaký směr a velikost má výslednice po odstranění jednoho náboje z vrcholu.

• Odpověď

  Po odstranění náboje z jednoho vrcholu má výsledná síla stejnou velikost, jako velikost síly mezi středovým a odstraněným nábojem, směr výsledné síly je opačný než směr této síly.