Sbírka řešených úloh

Dielektrický výtah

Úloha číslo: 242

Dvě dlouhé koaxiální válcové trubky (o vnitřním poloměru a a vnějším poloměru b) jsou svisle postaveny do nádoby s olejem (relativní permitivita ε_r, hustota ρ). Vnitřní trubka je udržována na potenciálu U, druhá je uzemněna. Do jaké výšky h mezi trubkami vystoupí olej?

Použijte následující vztah: válcový kondenzátor délky l o vnějším poloměru b a vnitřním poloměru a vyplněný dielektrikem o permitivitě ε má kapacitu C

\[C = \frac{2\pi\varepsilon l}{\ln (b/a)}.\]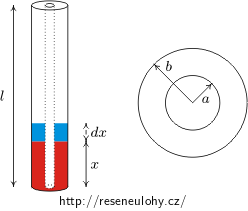

• Nápověda 1

  Olej vtahují dovnitř kondenzátoru síly elektrické povahy. Proti nim působí síla tíhová. Olej vystoupí do takové výšky, aby se tyto dvě síly vyrovnaly.

• Nápověda 2

  Změna energie kondenzátoru je rovna vykonané práci na vynesení dielektrika o výšku dx. Síla je potom derivací práce podle dráhy.

  Vypočtěte za tím účelem změnu kapacity kondenzátoru dC, jestliže dielektrikum stoupne z výšky x do výšky x+dx.

  Určete, k jaké změně energie kondenzátoru dojde, jestliže se kapacita změní o dC (změnou výšky kapaliny o dx). Přitom si uvědomte, že kondenzátor je připojený ke zdroji, a tudíž má mezi elektrodami stálé napětí.

• Nápověda 3

  Abyste mohli vypočítat změnu kapacity kondenzátoru, určete nejprve kapacitu kondenzátoru, pokud dielektrikum zabírá část délky x z celkové délky l válcového kondenzátoru. Užijte vztah v zadání a uvědomte si, že jde vlastně o dva paralelně spojené kondenzátory (jeden vyplněný vzduchem a druhý dielektrikem — olejem).

  Poté do určeného vztahu pro kapacitu dosaďte x+dx namísto x a oba vztahy od sebe odečtěte. Získáte tak závislost změny kapacity kondenzátoru dC na malém posunutí hladiny kapaliny dx.

• Rozbor

  Zdroj, ke kterému je válcový kondenzátor připojen, může konat práci. Tato práce se spotřebovává na vytahování dielektrika do prostoru mezi trubičkami. Vykonaná práce se projeví zvýšením energie kondenzátoru.

  Síly, které dielektrikum vtahují mezi trubičky, jsou elektrické povahy. Mechanismus jejich působení je složitý, nespočítáme je tedy přímo ze znalosti elektrického pole.

  Namísto toho použijeme úvahy, že síla je rovná derivaci vykonané práce na dielektrikum podle posunutí. Práce vykonaná na dielektriku se totiž projeví změnou elektrické energie kondenzátoru a tuto změnu jsme schopni spočítat podle známých vztahů.

  Strategie řešení úlohy je tedy následující: vypočteme, o jakou hodnotu dE se změní energie kondenzátoru při malém posunutí dx dielektrika vzhůru. Energie dE se rovná práci vykonané elektrickými silami, a tudíž podíl dE/dx určuje velikost působících elektrických sil.

  Pokud by nebyla přítomna gravitace, pak by olej vyplnil celý kondenzátor. Proti elektrickým silám však působí síla tíhová. Olej vystoupí do takové výše, kde se tyto dvě síly vyrovnají.

• Řešení

  Jestliže l je celková výška trubek, potom trubky společně s mezerou vyplněnou zčásti vzduchem a zčásti olejem (do výšky x) tvoří válcový kondenzátor o kapacitě:

  \[C = C_\mathrm{olej} + C_\mathrm{vzduch} = 2\pi\varepsilon\,\frac{x}{\ln (b/a)}+ 2\pi\varepsilon_0\,\frac{l-x}{\ln (b/a)} = 2\pi\varepsilon_0\,\frac{\varepsilon_r x}{\ln (b/a)} + 2\pi\varepsilon_0\,\frac{l-x}{\ln (b/a)} = 2\pi\varepsilon_0\,\frac{(\varepsilon_r-1)x+l}{\ln (b/a)}\ .\]

  Vztah vyplývá z faktu, že jde vlastně o paralelní spojení dvou kondenzátorů (jednoho délky x vyplněného olejem a druhého délky l-x vyplněného vzduchem).

  Jestliže nyní hladina oleje v kondenzátoru stoupne o výšku dx, pak se kapacita změní o hodnotu:

  \[{\rm d}C = 2\pi\varepsilon_0\,\frac{(\varepsilon_r-1)(x+{\rm d}x)+l}{\ln (b/a)} - 2\pi\varepsilon_0\,\frac{(\varepsilon_r-1)x+l}{\ln (b/a)} = 2\pi\varepsilon_0\,\frac{(\varepsilon_r-1){\rm d}x}{\ln (b/a)}.\]

  Tato změna má za následek změnu energie kondenzátoru:

  \[{\rm d}E = \frac{1}{2}U^2\,{\rm d}C,\]

  která odpovídá vykonání práce

  \[{\rm d}E = {\rm d}W = F\,{\rm d}x,\]

  kterou vykonala síla F působící na dielektrikum. Dostáváme tak

  \[F = \frac{{\rm d}W}{{\rm d}x} = \frac{{\rm d}E}{{\rm d}x} = \frac{1}{2}U^2\frac{{\rm d}C}{{\rm d}x} = \frac{1}{2}U^22\pi\varepsilon_0\frac{\varepsilon_r-1}{\ln (b/a)}.\]

  Tím jsme spočetli, jak na dielektrikum působí elektrické síly. Tyto síly dielektrikum vtahují dovnitř kondenzátoru až do chvíle, než je tíhová síla vykompenzuje. V tu chvíli platí

  \[F = F_\mathrm{G} = mg = \varrho\pi(b^2-a^2)gh,\]

  odkud vyplývá

  \[h = \frac{\varepsilon_0(\varepsilon_r-1)U^2}{\varrho(b^2-a^2)g\ln (b/a)}.\]

• Komentář

  Elektrické síly působící na dielektrikum jsou způsobené nehomogenitou pole na rozhraní, což je obtížné exaktně spočítat, ale díky úvaze s energií jsme se bez toho obešli.

• Odpověď

  Olej vystoupí do výšky

  \[h=\frac{\varepsilon_0(\varepsilon_\mathrm{r}-1)U^2}{\varrho(b^2-a^2)g\ln{(b/a)}}.\]

• Odkaz na podobnou úlohu

  Jiný způsob řešení naleznete v podobné úloze Kondenzátor s olejem, ve které je místo válcového kondenzátoru kondenzátor deskový.