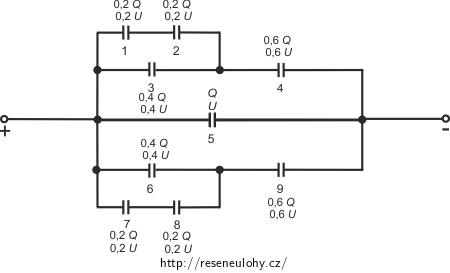
Spojování kondenzátorů II
Úloha číslo: 2015
Kondenzátory o téže kapacitě C jsou zapojeny podle obrázku. Určete výslednou kapacitu. Dále určete napětí a náboje na deskách jednotlivých kondenzátorů, jestliže na celém zapojení je napětí U.
Nápověda
Pokud si nejste jisti, jak se obvody s kondenzátory řeší, projděte si úlohu Spojování kondenzátorů I.
Klíčem k úspěchu je překreslení celého obvodu do „obvyklejšího tvaru“ tak, aby se zapojení nezměnilo, ale bylo lépe vidět, který kondenzátor je s kterým zapojen paralelně, resp. sériově.
Pokud si s překreslením nevíte rady, pomůžou vám úlohy Netradiční obvody 1 a Netradiční obvody 2.
Řešení – kapacita
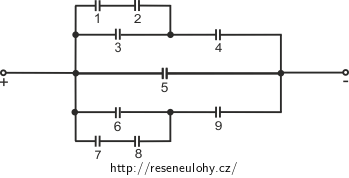
Schéma kondenzátorů překreslíme do obvyklejšího tvaru a pro přehlednost výpočtu si je očíslujeme.
V této úloze volíme analogický postup jako ve Spojování kondenzátorů I. Je-li tato úloha pro vás náročná, projděte si nejprve Spojování kondenzátorů I, kde je postup vysvětlen detailněji.
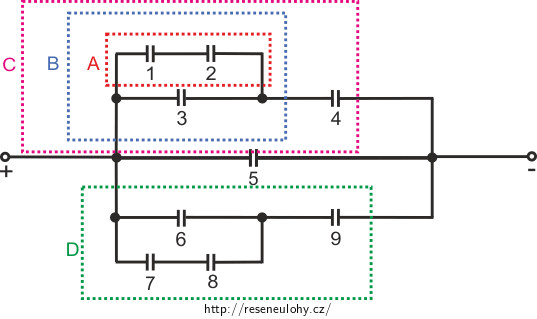
Nyní budeme kondenzátory postupně spojovat využitím vztahů pro paralelní a sériové zapojení (viz Spojování kondenzátorů I, Řešení nápovědy – kapacita a Spojování kondenzátorů I, Řešení nápovědy – napětí a náboj). Využijeme také symetrii obvodu, abychom některé výpočty nemuseli provádět dvakrát (všechny kondenzátory mají stejnou kapacitu C).
Kondenzátory 1 a 2 jsou zapojeny sériově:
\[\frac {1} {C_{1{,}2}} = \frac {1} {C} + \frac {1} {C},\] \[C_\mathrm{A}={C_{1{,}2}} = \frac {C} {2}.\]Kondenzátory A a 3 jsou zapojeny paralelně:
\[C_\mathrm{A,3} = C_\mathrm{A} + C,\] \[C_\mathrm{B}=C_\mathrm{A,3} = \frac {3}{2}C.\]Kondenzátory B a 4 jsou zapojeny sériově:
\[\frac {1}{C_\mathrm{B,4}}= \frac {1}{C_\mathrm{B}} + \frac {1} {C_4} = \frac {2} {3C} +\frac {1}{C},\] \[C_\mathrm{C} = C_\mathrm{B,4} = \frac {3} {5} C.\]Díky tomu, že je obvod symetrický, můžeme napsat:
\[C_\mathrm{D} = C_\mathrm{C}= \frac {3} {5} C.\]Nyní si můžeme obvod opět překreslit.
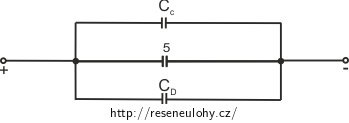
Kondenzátory \(C_\mathrm{C}, C_\mathrm{D}\) a 5 jsou zapojeny paralelně:
\[C_\mathrm{C, D, 5} = C_\mathrm{C} + C_\mathrm{D} + C_5=\frac{3}{5}C + \frac{3}{5}C +C ,\] \[C_\mathrm{V} = C_\mathrm{C, D, 5} = \frac {11}{5}C.\]Výsledná kapacita zapojení \(C_\mathrm{V} = \frac {11} {5} C.\)
Nápověda – vztahy pro napětí a náboj na kondenzátorech
Mezi kapacitou, nábojem a napětím kondenzátoru platí vztah (zavedení kapacity kondenzátoru)
\[Q = UC.\]Při sériovém zapojení kondenzátorů je na všech kondenzátorech stejný náboj. Napětí se v tomto případě sčítají:
\[Q = Q_1 = Q_2,\] \[U = U_1 + U_2.\]Při paralelním zapojení se náboje na jednotlivých kondenzátorech sčítají. Napětí je na všech kondenzátorech stejné:
\[Q = Q_1 + Q_2,\] \[U = U_1 = U_2.\]Při výpočtu napětí a nábojů budeme postupovat opačně než při výpočtu celkové kapacity. Začneme obvodem, kde jsou všechny kondenzátory nahrazeny jedním, a postupně se budeme vracet k „původnímu“ zapojení.
Řešení – napětí a náboj

Nyní se vraťme k obvodu s kondenzátory C, D a 5. Napětí na těchto kondenzátorech je stejné (viz nápověda) a je stejné jako napětí U na celém zapojení:
\[U_\mathrm{C} = U_\mathrm{D} = U_5 = U.\]Abychom spočítali náboje, využijeme obecný vztah
\[Q = U C.\tag{1}\]Takže dostáváme
\[Q_\mathrm{C}=C_C U=\frac {3} {5} C U,\] \[Q_\mathrm{D}=C_D U=\frac {3} {5} C U,\] \[Q_5= C U.\]
Kondenzátor C vznikl spojením sériově zapojených kondenzátorů 4 a B. Náboje na sériově zapojených kondenzátorech jsou stejné:
\[Q_4 = Q_B = Q_C=\frac {3} {5} C U. \]Napětí spočítáme ze vztahu (1)
\[U_4 = \frac {Q_4}{C_4} = \frac {3}{5}U,\] \[U_\mathrm{B} = \frac {Q_4}{C_B} = \frac {2}{5}U.\]Kondenzátor B vznikl spojením paralelně zapojených kondenzátorů 3 a A. Napětí na paralelně zapojených kondenzátorech jsou stejná:
\[U_3 = U_\mathrm{A} = U_\mathrm{B} = \frac {2} {5}U.\]Náboje spočítáme ze vztahu (1)
\[Q_3 = C_3 U_3 = \frac {2} {5}CU,\] \[Q_\mathrm{A} = C_\mathrm{A} U_\mathrm{A} = \frac {1} {5}CU.\]Kondenzátor A vznikl spojením sériově zapojených kondenzátorů 1 a 2. Náboje na sériově zapojených kondenzátorech jsou stejné:
\[Q_1 = Q_2 = Q_\mathrm{A} = \frac {1} {5} CU.\]Napětí spočítáme ze vztahu (1)
\[U_1 = \frac {Q_1}{C_1} = \frac {1} {5} U,\] \[U_2 = \frac {Q_2}{C_2} = \frac {1} {5} U.\]Jelikož je obvod souměrný (a kondenzátory mají stejnou kapacitu), nemusíme již dopočítávat náboje a napětí na kondenzátorech 6, 7, 8 a 9. Hodnoty budou odpovídat hodnotám kondenzátorů souměrných podle osy. Tedy například napětí a náboj na kondenzátoru 1 je stejný jako na kondenzátoru 7.
Odpověď
Celková kapacita zapojení \(C_\mathrm{V} = \frac {11} {5}C.\)
Náboje a napětí na jednotlivých kondenzátorech:
\[Q_1 = Q_7= \frac {1} {5}CU \quad Q_2=Q_8 = \frac {1} {5}CU \qquad Q_3=Q_6 =\frac{2}{5}CU \qquad Q_4=Q_9 =\frac {3} {5} CU \qquad Q_5 = CU \] \[U_1=U_7= \frac {1} {5}U \qquad U_2=U_8 = \frac {1} {5}U \qquad U_3=U_6 = \frac {2}{5}U \qquad U_4=U_9 = \frac {3} {5} U \qquad U_5 = U. \]V následujícím schématu je použito označení \(Q=UC\), kde U je napětí zdroje a C je kapacita každého z kondenzátorů.