Sbírka řešených úloh

Netradiční obvody 1

Úloha číslo: 276

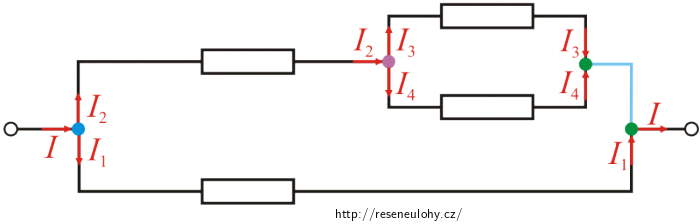
Jaký je výsledný elektrický odpor níže překreslených obvodů, jestliže všechny zapojené rezistory mají odpor R?

a)

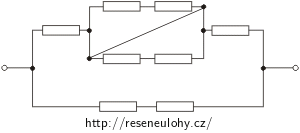
b)

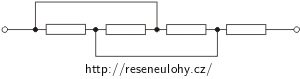
c)

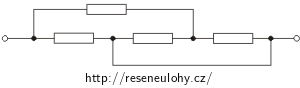
• Nápověda 1

  Základem úspěchu při řešení je překreslit si obvod do „přehlednější“ či obvyklejší podoby. Tedy tak, aby bylo jasné, zda se jedná o sériové nebo paralelní zapojení rezistorů.

• Nápověda 2

  „Ohýbání“ vodičů při překreslování obvodů nijak nemění vlastnosti obvodu a tedy ani celkový odpor.

  Pokud je rezistor zkratován vodičem, neteče jím proud. Rezistory, kterými neteče proud, můžeme z obvodu vynechat.

• Rozbor

  Při výpočtu celkových odporů daných zapojení je důležité si vše správně překreslit do „názornější“ podoby. Na to neexistuje obecný návod, který by bylo možné použít pro různé obvody. Proto zde uvedeme dva triky, které lze často využít.

  1. Pokud vodič propojuje dva uzly a není na něm umístěn žádný spotřebič (rezistor), můžeme oba uzly sloučit do jediného. Tedy např. pro schéma a znázorňují následující dva obrázky stejné zapojení:

  

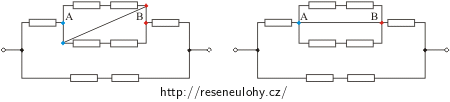
  2. V druhém obrázku nyní řešíme následující problém: máme zde část obvodu spojenou paralelně a jedna z paralelních větví není zatížená žádným spotřebičem, a tudíž nemá žádný odpor (část obvodu je tímto vodičem zkratována). Touto větví bude protékat všechen proud, který vstupuje do uzlu A. Dalšími dvěma větvemi tedy neprotéká žádný proud a nebudou tak mít vliv na celkový odpor paralelní části – odpor paralelní části je proto nulový. (Pozn.: Ke stejné úvaze bychom došli i kdybychom se řídili předchozím pravidlem a uzly A a B jsme sjednotili.)

  Pomocí podobných úvah budeme řešit i zbývající zapojení.

  Při výpočtu celkového odporu zapojení využijeme tato pravidla:

  1. Pro sériově zapojené rezistory (zapojení za sebou) je celkový odpor roven součtu odporů jednotlivých rezistorů.
  2. Pro paralelně spojené rezistory platí, že převrácenou hodnotu celkového odporu získáme jako součet převrácených hodnot jednotlivých rezistorů.

• Řešení části a)

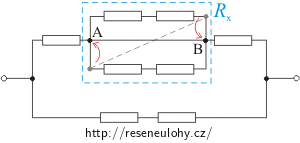
  Obvod si díky následujícím poznatkům překreslíme do vhodnější podoby:

  Uzly vodiče, který v paralelní části obvodu R_x tvoří úhlopříčku, můžeme ztotožnit s uzly A, B paralelní části obvodu (uzly leží na stejném vodiči a není mezi nimi připojen žádný spotřebič).

  

  Nyní se blíže podíváme na paralelní část obvodu označenou R_x. Z obrázku je patrné, že tuto část tvoří tři paralelní větve. Jedna z těchto větví není zatížena žádným rezistorem. Má tedy nulový odpor a protéká jí celý proud, který vstupuje do uzlu A. Dalšími dvěma větvemi neprotéká žádný proud (jsou vodičem „vyzkratované“), a nemají tedy vliv na celkový odpor paralelní části R_x:

  \[R_\mathrm{x}\,=\,0\,\mathrm{\Omega}.\]

  Protože část R_x má nulový odpor, bude celkový odpor schématu stejný jako pro dvě paralelní větve, kde na každé větvi jsou sériově zapojeny dva rezistory. Pro tyto paralelní větve tedy platí:

  \[R_\mathrm{h}\,=\,R+R\,=\,2R\tag{horní větev}\] \[R_\mathrm{d}\,=\,R_\mathrm{h}\,=\,2R\,.\tag{dolní větev}\]

  A pro celkový odpor schématu:

  \[\frac{1}{R_\mathrm{celk}}\,=\,\frac{1}{R_\mathrm{h}}+\frac{1}{R_\mathrm{d}}\,=\,\frac{1}{2R}+\frac{1}{2R}\,=\,\frac{2}{2R}\,=\,\frac{1}{R}\] \[R_\mathrm{celk}\,=\,R\,.\]

• Dynamický prvek – překreslení obvodu a)

  Následující aplet zobrazuje animaci překreslení obvodu.

• Řešení části b)

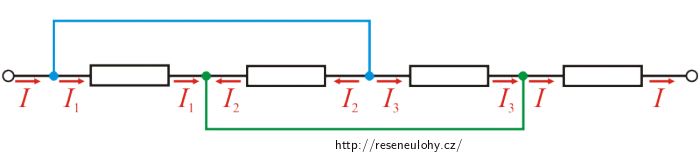
  Stejně jako v minulém oddíle můžeme i u tohoto zapojení sloučit některé uzly (v obrázku jsou vyznačeny barevně). Dále si do obrázku dopíšeme proudy vstupující a vystupující z jednotlivých uzlů.

  

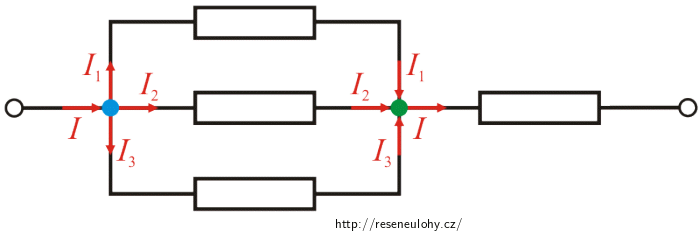
  Nyní si schéma ještě jednou překreslíme. Na obrázku vidíme, že v modrém uzlu se proud I dělí na tři části I₁, I₂, I₃. Ty se pak opět sloučí v zeleném uzlu. Tedy:

  

  Nyní již můžeme vypočítat celkový odpor zapojení jako součet odporu rezistoru R a odporu paralelní části.

  Pro odpor paralelní části R_p platí:

  \[\frac{1}{R_\mathrm{p}}\,=\,\frac{1}{R}+\frac{1}{R}+\frac{1}{R}\,=\,\frac{3}{R}\] \[R_\mathrm{p}\,=\,\frac{R}{3}\,.\]

  Celkový odpor zapojení:

  \[R_\mathrm{celk}\,=\,R_\mathrm{p}\,+\,R\,=\,\frac{R}{3}\,+\,R\] \[R_\mathrm{celk}\,=\,\frac{4R}{3}\,.\]

• Dynamický prvek – překreslení obvodu b)

  Následující aplet zobrazuje animaci překreslení obvodu.

• Řešení části c)

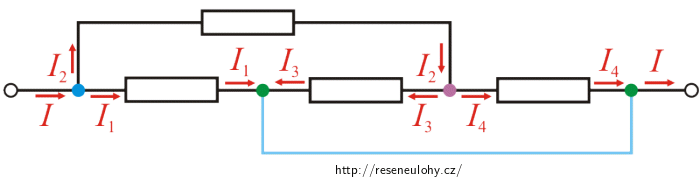
  I v tomto zapojení do obrázku barevně označíme jednotlivé uzly a dopíšeme proudy. Uzly, ze kterých vychází větev bez připojeného rezistoru (na obrázku označena modře), označíme jednou barvou. Jedná se totiž o „stejné“ uzly a oba bychom mohli spojit do jediného.

  

  Nyní si toto zapojení ještě jednou překreslíme. Na obrázku vidíme, že v modrém uzlu se proud I dělí na proudy I₁ a I₂. Proud I₂ se dále ve fialovém uzlu dělí na proud I₃ a I₄.

  

  Nyní vypočítáme celkový odpor zapojení. Připomeňme, že všechny rezistory v zapojení mají odpor R.

  V horní větvi schématu jsou tři rezistory. Dva jsou zapojeny paralelně a třetí je k nim připojen do série. Pro celkový odpor R_p dvou paralelně zapojených rezistorů platí:

  \[ \frac{1}{R_\mathrm{p}}\,=\,\frac{1}{R}\,+\,\frac{1}{R}\,=\,\frac{2}{R} \] \[ R_\mathrm{p}\,=\,\frac{R}{2}\,. \]

  Celkový odpor R_h horní větve zapojení se rovná součtu odporu jednoho rezistoru a odporu paralelní části:

  \[ R_\mathrm{h}\,=\,R\,+\,R_\mathrm{p}\,=\,R\,+\,\frac{R}{2} \] \[ R_\mathrm{h}\,=\,\frac{3R}{2}\,. \tag{horní větev}\]

  Dolní větev zapojení je tvořena jediným rezistorem. Její odpor se tedy rovná odporu tohoto rezistoru:

  \[ R_\mathrm{d}\,=\,R\,. \tag{dolní větev}\]

  Celkový odpor schématu:

  \[ \frac{1}{R_\mathrm{celk}}\,=\,\frac{1}{R_\mathrm{h}}\,+\,\frac{1}{R_\mathrm{d}}\,=\,\frac{2}{3R}\,+\,\frac{1}{R}\,=\,\frac{5}{3R} \] \[ R_\mathrm{celk}\,=\,\frac{3R}{5}\,. \]

• Dynamický prvek – překreslení obvodu c)

  Následující aplet zobrazuje animaci překreslení obvodu.

• Odpověď

  Celkové odpory jednotlivých zapojení jsou: a) \(R\), b) \(\frac{4R}{3}\), c) \(\frac{3R}{5}\).

• Odkaz na podobnou úlohu

  V úloze Netradiční obvody 2 zkuste vypočítat celkový odpor dalších tří obvodů.