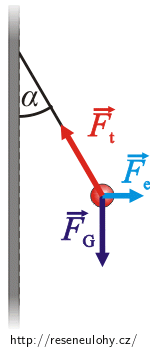
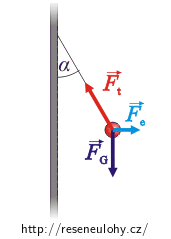
Zavěšená kulička v poli nabité desky
Úloha číslo: 760
Nekonečně velká svislá deska je nabita rovnoměrně nábojem o plošné hustotě 3·10−5 C m−2. V jednom bodě desky je upevněno hedvábné vlákno, na němž je zavěšena kulička o hmotnosti 1 g.
Jaký náboj nese kulička, svírá-li vlákno s rovinou desky úhel 30°?
Nápověda: Elektrické pole v okolí nabité desky
Nabitá deska kolem sebe vytváří homogenní elektrické pole o intenzitě \(E\,=\, \frac{\sigma}{2\varepsilon_0}\). Vektor intenzity míří od desky.
Pole v okolí nekonečné nabité desky se řeší v úloze Pole rovnoměrně nabité roviny.
Nápověda
Nakreslete si obrázek celé situace a působících sil.
Co platí pro síly, jestliže je kulička v klidu?
Rozbor
Nabitá deska kolem sebe vytváří homogenní elektrické pole, které působí na nabitou kuličku odpudivou elektrickou silou. Tato síla míří od desky.
Na kuličku na vlákně tedy působí tíhová síla, tahová síla vlákna a elektrická síla. Protože je kulička v klidu, musí být výslednice těchto sil rovna nule.
Velikost náboje vyjádříme z poměru elektrické a tíhové síly.
Řešení
Nabitá deska kolem sebe vytváří homogenní elektrické pole o intenzitě:
\[E\,=\,\frac{\sigma}{2 \varepsilon_0}\,.\tag{1}\]Toto pole působí na nabitou kuličku elektrickou silou, která míří od desky (podrobnější odvození naleznete v úloze Pole rovnoměrně nabité roviny).
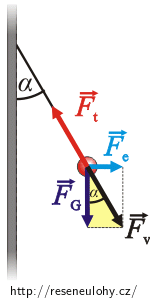
Na kuličku zavěšenou na vlákně tedy působí tíhová síla \( \vec{F}_\mathrm{G}\), tahová síla vlákna \(\vec{F}_\mathrm{t}\) a elektrická síla \( \vec{F}_\mathrm{e}\).
Protože je kulička v klidu, musí být výslednice těchto sil rovna nule. Tahová síla vlákna je tedy stejně velká jako výslednice elektrické a tíhové síly a má opačný směr (viz obrázek).
Ze žlutého trojúhelníka vyjádříme poměr elektrické a tíhové síly:
\[\mathrm{tg}\,\,\alpha\,=\,\frac{F_\mathrm{e}}{F_\mathrm{G}}.\]Velikost sil vypočítáme ze vztahů Fe = EQ a FG = mg.
Nakonec vyjádříme hledaný náboj Q:
\[\mathrm{tg}\,\,\alpha\,=\,\frac{EQ}{mg}.\]Za intenzitu elektrického pole dosadíme ze vztahu (1) a zlomek upravíme:
\[\mathrm{tg}\,\,\alpha\,=\,\frac{\frac{\sigma}{2\varepsilon_0}Q}{mg}\,=\,\frac{\sigma Q}{2\varepsilon_0 mg},\] \[Q\,=\,\frac{2\varepsilon_0 mg\, \mathrm{tg}\,\alpha}{\sigma}.\]Zápis a číselný výpočet
σ = 3·10−5 C m−2 plošná hustota náboje na desce m = 1 g = 10−3 kg hmotnost kuličky α = 30° úhel, který svírá vlákno s rovinou desky Z tabulek g = 9,81 m s−2 tíhové zrychlení ε0 = 8,85·10−12 C2N−1m−2 permitivita vakua
\[ \begin{eqnarray} Q\,&=&\,\frac{2\varepsilon_0 mg\, \mathrm{tg}\,\alpha}{\sigma}\,=\,\frac{2\,\cdot \,8{,}85 {\cdot} 10^{-12}\, \cdot \,10^{-3}\cdot 9{,}81\, \cdot \mathrm{tg}\,30^\circ}{3{\cdot}10^{-5}}\,\mathrm{C}\\ Q\,&\dot=&\,3{,}3{\cdot} 10^{-9}\,\mathrm{C}\dot=\,3{,}3\,\mathrm{nC} \end{eqnarray}\]Odpověď
Kulička je nabita nábojem 3,3 nC.