Pole nabité přímky
Úloha číslo: 534
Nekonečně dlouhá přímka je rovnoměrně nabita nábojem s délkovou hustotou λ.
1) Najděte vztah pro intenzitu elektrického pole ve vzdálenosti z od přímky.
2) Určete také potenciál ve vzdálenosti z od přímky.
Nápověda: Intenzita elektrického pole
Protože k řešení úlohy se vzhledem k její symetrii hodí využít Gaussovu větu, je třeba si rozmyslet, jak zvolit vhodnou Gaussovu plochu.
Nápověda: Potenciál
Potenciál je roven potenciální energii vztažené na jednotkový náboj:
\[\varphi\,=\, \frac{E_\mathrm{p}}{Q}\]a potenciální energie je rovna záporně vzaté práci, kterou musí vykonat elektrická síla, aby přenesla náboj z místa s nulovou potenciální energií (v našem případě si toto místo zvolíme ve vzdálenosti a od přímky) do daného místa:
\[E_\mathrm{p}(z)\,=\, - \int^\mathrm{z}_\mathrm{a} \vec{F} \cdot \mathrm{d}\vec{z}.\]Pozn.: Pokud bychom volili nulový potenciál v nekonečnu jako u většiny úloh, nemohli bychom integrál dopočítat. Podobně jako v úloze Pole rovnoměrně nabité roviny, viz její oddíl Potenciál.
Obě strany rovnice vydělíme nábojem Q a dostaneme:
\[\varphi\,=\, - \int^\mathrm{z}_\mathrm{a} \frac{\vec{F}} {Q}\cdot \mathrm{d}\vec{z}\,.\]Podíl síly \(\vec{F}\) a náboje Q je roven intenzitě elektrického pole \(\vec{E}\):
\[\varphi\,=\, - \int^\mathrm{z}_\mathrm{a} \vec{E}\cdot \mathrm{d}\vec{z}.\]Rozbor
Vzhledem k symetrickému rozložení náboje je nejjednodušším způsobem nalezení intenzity elektrického pole v tomto případě využití Gaussovy věty. Gaussova věta vyjadřuje vztah mezi tokem elektrické intenzity uzavřenou plochou a celkovým nábojem, který se nachází uvnitř této plochy.
Ze symetrie rozložení náboje plyne, že vektor elektrické intenzity míří ve všech místech od přímky a jeho velikost závisí pouze na vzdálenosti od přímky. Důvodem je symetrické rozložení náboje na přímce.
Jako Gaussovu plochu zvolíme povrch válce, jehož osa splývá s nabitou přímkou. V tomto případě má vektor elektrické intenzity na celé ploše pláště válce stejnou velikost a je na ni kolmý. Naopak s podstavami válce je vektor intenzity rovnoběžný, proto je tok intenzity podstavami roven nule. Tím se nám zjednoduší výpočet celkového toku intenzity. Uvnitř Gaussovy plochy je uzavřena část přímky, a tím i odpovídající část náboje.
Potenciál vypočítáme z elektrické intenzity. Potenciál v daném místě se až na znaménko rovná integrálu intenzity z místa s nulovým potenciálem do tohoto místa. Nulový potenciál zvolíme ve vzdálenosti a od přímky. (Podrobnější vysvětlení je uvedeno v nápovědě.)
Řešení: Intenzita
V tomto oddíle určíme intenzitu ve vzdálenosti z od přímky.
Využijeme Gaussovu větu:
\[\oint_\mathrm{S} \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0},\] \[\oint_\mathrm{S} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}.\tag{*}\]Náboj je na přímce rozložen rovnoměrně, proto je elektrické pole vytvořené přímkou symetrické. Vektor elektrické intenzity míří ve všech místech od přímky (tj. je na ni kolmý) a jeho velikost závisí pouze na vzdálenosti od přímky.
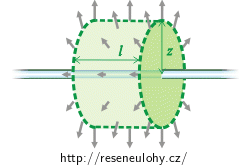
Jako Gaussovu plochu volíme povrch válce (na obrázcích vyznačen zeleně), jehož osa splývá s přímkou. Celkový tok intenzity plochou získáme sečtením toku podstavami a pláštěm válce.
Tok podstavami:Vektor elektrické intenzity je rovnoběžný s podstavami Gaussova válce a tok elektrické intenzity podstavami je tedy nulový. Celkový tok intenzity Gaussovou plochou se rovná pouze toku pláštěm válce.
Tok pláštěm:Vektor elektrické intenzity je kolmý k povrchu pláště válce, a proto platí \(\vec{E} \cdot \vec{n}\,=\,En\,=\,E\) (pozn. \(\vec{n}\) je jednotkový vektor).
S využitím tohoto poznatku můžeme vyjádřit tok intenzity pláštěm a upravit integrál na levé straně Gaussovy věty:
\[\oint_\mathrm{pl} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,\oint_\mathrm{pl} E n\mathrm{d}S\,=\, \oint_\mathrm{pl} E\mathrm{d}S\,.\]Velikost vektoru elektrické intenzity E je ve všech místech pláště Gaussova válce stejná, a proto ji můžeme vyjmout před integrál jako konstantu. Dostáváme tedy vztah
\[\oint_\mathrm{pl} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E \oint_\mathrm{pl} \mathrm{d}S\,=\,E S_\mathrm{pl}\,,\]kde Spl = 2πzl je obsah pláště Gaussova válce (l je délka válce):
\[\oint_\mathrm{pl} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E\, 2 \pi z l.\]Výsledný vztah dosadíme zpět do Gaussovy věty (*):
\[E 2 \pi z l\,=\, \frac{Q}{\varepsilon_0}.\]Vyjádříme velikost intenzity:
\[E \,=\, \frac{Q}{2 \pi \varepsilon_0 z l}.\tag{**}\]Zbývá vyjádřit náboj Q uvnitř zvolené Gaussovy plochy pomocí zadaných veličin.
Uvnitř plochy je část přímky o délce l, náboj tedy můžeme vyjádřit pomocí její délky a délkové hustoty náboje λ:
\[Q\,=\,\lambda l.\]Dosadíme do vzorce (**):
\[E \,=\, \frac{\lambda l}{2 \pi \varepsilon_0 z l}\]a upravíme. Ve vzdálenosti z má elektrické pole nabité přímky intenzitu:
\[E \,=\, \frac{ \lambda }{2 \pi \varepsilon_0\,z }\,.\]Vidíme, že velikost intenzity E nabité přímky tedy lineárně klesá se vzdáleností z od přímky.
Řešení: Potenciál
Potenciál v daném místě se až na znaménko rovná integrálu intenzity z místa s nulovým potenciálem do daného bodu. Nulový potenciál zvolíme ve vzdálenosti a od přímky (podrobnější vysvětlení je uvedeno v nápovědě):
\[\varphi (z)\,=\, - \int_\mathrm{a}^\mathrm{z} \vec{E} \cdot \mathrm{d}\vec{z}.\]Pozn.: Pokud bychom volili nulový potenciál v nekonečnu jako u většiny úloh, nemohli bychom integrál dopočítat. Podobně jako v úloze Pole rovnoměrně nabité roviny, viz její oddíl Potenciál.
Potenciál nezávisí na volbě integrační cesty, proto ji můžeme volit libovolně. V této úloze jako integrační cestu zvolíme část přímky, která je kolmá na nabitou přímku.
Vektor elektrické intenzity \(\vec{E}\) je rovnoběžný s vektorem \(\vec{z}\), proto můžeme integrál zjednodušit:
\[ \varphi (z)\,=\, - \int^\mathrm{z}_\mathrm{a} E \mathrm{d}z. \]Do integrálu dosadíme velikost intenzity, kterou jsme si vyjádřili v předchozím oddíle, a vytkneme před integrál všechny konstanty:
\[\varphi (z)\,=\, - \int^\mathrm{z}_\mathrm{a} \frac{\lambda}{2 \pi \varepsilon_0}\,\frac{1}{z}\, \mathrm{d}z \,=\, - \frac{\lambda}{2\pi \varepsilon_0} \int^\mathrm{z}_\mathrm{a}\frac{1}{z}\, \mathrm{d}z\,.\]Vypočítáme integrál:
\[\varphi (z)\,=\,- \,\frac{\lambda}{2\pi\varepsilon_0}\left[\ln z\right]^z_{a}\,.\]Dosadíme meze integrálu a vytkneme konstanty:
\[\varphi (z)\,=\,-\frac{\lambda}{2\pi\varepsilon_0}\, \ln z\,+\,\frac{\lambda}{2\pi\varepsilon_0}\, \ln a\,=\,\frac{\lambda}{2\pi\varepsilon_0}\, \left(\ln a\,-\, \ln z\right)\,.\]Rozdíl logaritmů je logaritmus podílu:
\[\varphi (z)\,=\,\frac{\lambda}{2\pi\varepsilon_0}\, \ln \frac{a}{z}.\]Získali jsme velikost potenciálu vně válce ve vzdálenosti z.
Odpověď
Pro velikost intenzity ve vzdálenosti z od přímky platí vztah
\[E \,=\, \frac{\lambda}{2 \pi \varepsilon_0 \,z}\,.\]Vektor elektrické intenzity míří od přímky (jestliže je náboj přímky kladný).
Elektrický potenciál pole nabité přímky je dán vztahem
\[\varphi (z)\,=\,\frac{\lambda}{2\pi\varepsilon_0}\, \ln \frac{a}{z}\,.\]Grafy
Při kreslení grafů uvažujeme, že je přímka nabita kladným nábojem.
Graf závislosti velikosti el. intenzity na vzdálenosti od osy válce
Ve vzdálenosti z od přímky míří vektor směrem od přímky a má velikost
\[E \,=\, \frac{ \lambda}{ 2\pi \varepsilon_0\,z}\,.\]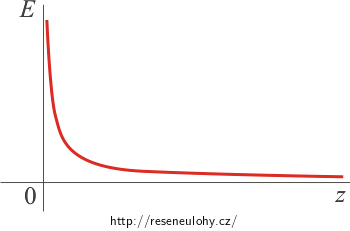
Graf funkce je spojitý. Jedná se o nepřímou úměrnost, tj. grafem je jedna větev hyperboly.
Pozn.: Intenzita elektrického pole je spojitá s výjimkou bodů, kdy prochází nabitou plochou. Při průchodu nabitou plochou zůstávají spojité pouze tečné složky vektoru intenzity. Normálové složky se mění „skokem“, který je úměrný plošné hustotě náboje. V této úloze žádné nabité plochy nemáme.
Graf závislosti el. potenciálu na vzdálenosti od osy válce
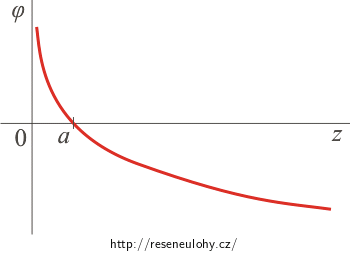
Elektrický potenciál ve vzdálenosti z má velikost
\[\varphi (z)\,=\,\frac{\lambda}{2\pi \varepsilon_0}\, \ln \frac{a}{z}\,.\]Funkce je na celém intervalu spojitá. Osu z protíná v bodě a, kde jsme si zvolili nulový potenciál.
Pozn.: Elektrický potenciál je vždy spojitý, protože se jedná vlastně o práci při přenášení jednotkového náboje a ta se nemůže změnit „skokově“. Kromě bodů na nabitých plochách má potenciál spojité také první derivace, tj. je hladký.
Odkaz: Jak jinak vypočítat intenzitu v okolí přímky?
Intenzita elektrického pole přímky se dá vypočítat také přímou integrací. Tento postup je uveden v úloze Nabitá úsečka 2.




