Indukčnost cívky rotující v magnetickém poli
Úloha číslo: 476
Válcová cívka dlouhá 10 cm se 600 závity a poloměrem 2 cm rotuje v magnetickém poli o magnetické indukci 3·10-3 T. Určete:
a) maximální indukční tok vnitřkem cívky,
b) indukčnost cívky.
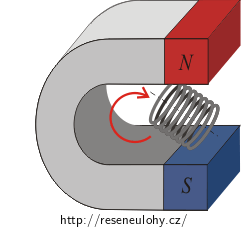
Nápověda a) Maximální hodnota magnetického indukčního toku
Magnetický indukční tok cívkou bude největší, pokud závity cívky bude procházet „co nejvíce“ magnetických indukčních čar.
Uvědomte si, v jaké poloze vůči vektoru magnetické indukce musí být umístěna cívka, aby byl magnetický indukční tok cívkou maximální.
Nápověda b) Co je indukčnost cívky
Indukčnost cívky je skalární veličina, která charakterizuje vlastní indukci v uzavřeném vodiči, např. v cívce. Uzavřený vodič, kterým prochází proud I, vytváří kolem sebe magnetické pole, pro které můžeme určit magnetický indukční tok Φ daným vodičem. Indukčnost vodiče je potom dána vztahem
\[L=\frac{\Phi}{I}.\]Magnetické pole je úměrné velikosti elektrického proudu vodičem a magnetický indukční tok je úměrný magnetickému poli. Z toho plyne, že indukčnost nezávisí na proudu. Její hodnota je dána jen tvarem a uspořádáním vodiče.
Jednotkou inukčnosti je henry – značka H.
Rozbor
Maximální indukční tok cívkou
Magnetický indukční tok cívkou bude největší, pokud závity cívky bude procházet „nejvíce“ magnetických indukčních čar. To nastane v případě, že vektor magnetické indukce bude kolmý na plochu závitu cívky.Indukčnost cívky
Protože se cívka otáčí v magnetickém poli, mění se magnetický indukční tok cívkou a v cívce se indukuje časově proměnný elektrický proud. Jestliže cívkou začne procházet proud, v jejím okolí se vytvoří magnetické pole. Magnetický indukční tok tohoto pole je úměrný indukovanému proudu. Konstanta úměrnosti mezi magnetickým indukčním tokem cívky a indukovaným proudem se nazývá indukčnost cívky.
Řešení a) Maximální indukční tok cívkou
Vyjádříme vztah pro magnetický indukční tok cívkou. Protože můžeme magnetické pole, ve kterém se nachází cívka, považovat za homogenní, magnetický indukční tok Φ cívkou je pak dán vztahem
\[\Phi=NBS\cos{\alpha},\]kde α je úhel mezi vektorem magnetické indukce \(\vec{B}\) a vektorem normály plochy \(\vec{S}.\)
Magnetický indukční tok cívkou bude maximální, pokud \(\cos{\alpha}=1\), tj \(\alpha=0^\circ\). Vektory \(\vec{B}\) a \(\vec{S}\) tedy budou rovnoběžné. To znamená, že vektor magnetické indukce \(\vec{B}\) je kolmý na plochu smyčky S. Maximální indukční tok cívkou má pak tvar
\[\Phi_\mathrm{max}=NBS.\]Plocha závitu cívky S se rovná obsahu kruhu o poloměru r.
Pro maximální indukční tok Φmax cívkou tak platí
\[\Phi_\mathrm{max}=\pi r^2 NB.\]Řešení b) Indukčnost cívky
Rotující cívka se nachází v magnetickém poli a díky němu se v ní indukuje napětí. Pokud je cívka propojena, bude se v ní indukovat i proud. Tento proud bude vytvářet další indukované magnetické pole, říkejme mu třeba pole cívky. Indukčnost L je konstanta úměrnosti mezi okamžitým magnetickým tokem pole cívky Φ a okamžitým proudem i, který cívkou prochází, tj.
\[\Phi(t)=Li(t).\tag{1}\]Budeme uvažovat polohu s největší hodnotou magnetického indukčního toku. V předchozím oddíle jsme odvodili, že magnetický indukční tok bude maximální, pokud bude vektor magnetické indukce kolmý na plochu cívky.
Pro magnetický indukční tok tak platí
\[\Phi=NBS.\]Za velikost magnetické indukce dosadíme vztah pro magnetickou indukci uvnitř dlouhé cívky:
\[B=\mu_\mathrm{0}\frac{N}{l}i.\]Dílčí vztahy dosadíme do rovnice (1):
\[NBS=Li,\] \[N\mu_\mathrm{0}\frac{N}{l}iS=Li\]a vyjádříme indukčnost cívky L:
\[L=\mu_\mathrm{0}\frac{N^2S}{l}.\]Zápis a číselné dosazení
\(l\,=\,10\,\mathrm{cm}=\,0{,}10\,\mathrm{m}\) délka cívky \(r\,=\,2\,\mathrm{cm}=\,0{,}02\,\mathrm{m}\) poloměr cívky \(B\,=\,3{\cdot}10^{-3}\,\mathrm{T}\) magnetická indukce pole \(N\,=\,600\) počet závitů cívky \(\Phi\,= \,?\,\mathrm{(Wb)}\) maximální indukční tok vnitřkem cívky \(L\,= \,?\,\mathrm{(H)}\) indukčnost cívky Z tabulek: \(\mu_\mathrm{0}\,= \,4\pi\cdot10^{-7}\,\mathrm{Hm^{-1}}\) permeabilita vakua
\[\Phi_\mathrm{max}=\pi r^2 NB=\pi\cdot0{,}02^2{\cdot}600\cdot 3{\cdot}10^{-3}\,\mathrm{Wb}\,\dot{=}\,2{\cdot}10^{-3}\,\mathrm{Wb}\] \[L=\mu_\mathrm{0}\pi\,\frac{(Nr)^2}{l}=4\cdot\pi^2{\cdot}10^{-7}\cdot\frac{(600{\cdot}0{,}02)^2}{0{,}10}\,\mathrm{H}\,\dot{=}\,6{\cdot}10^{-3}\,\mathrm{H}\]Odpověď
Maximální indukční tok, který bude procházet cívkou, má přibližně hodnotu 2 mWb.
Cívka má indukčnost přibližně 6 mH.





