Nehomogenní prostředí mezi válcovými elektrodami
Úloha číslo: 308
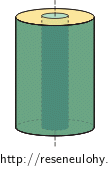
Prostor mezi dvěma souosými válcovými elektrodami o (velké) délce L a poloměrech a, b (a < b) je vyplněn materiálem, jehož vodivost σ se mění se vzdáleností od středu válce a lze ji popsat vztahem \(\sigma\left(r\right)\,=\,\frac{c}{r}\), kde a < r < b a c je konstanta.
Najděte celkový odpor materiálu mezi elektrodami.
Poznámka: Tuto úlohu zde řešíme dvěma způsoby:
I. Nápověda
Podívejte se na řešení podobné, o něco jednodušší úlohy Elektrický proud mezi válcovými elektrodami metodou přímé integrace odporů jednotlivých částí vodiče.
I. Rozbor
Prostor mezi válcovými elektrodami rozdělíme na tenké válcové slupky o poloměru r, kde a < r < b.
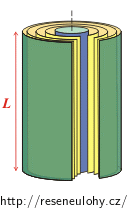
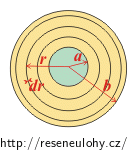
Celý vodič je vlastně sériovým zapojením těchto slupek. Celkový odpor materiálu mezi elektrodami tedy získáme jako součet odporů všech slupek.
Elektrický odpor jedné válcové slupky je závislý na délce a tloušťce slupky a na měrné elektrické vodivosti materiálu.
I. Řešení
Prostor mezi válcovými elektrodami rozdělíme na tenké válcové slupky o poloměru r (a < r < b). Celý vodič je tak sériovým zapojením těchto slupek.


Elektrický odpor R homogenního vodiče je nepřímo úměrný vodivosti materiálu σ. Velikost elektrického odporu vypočítáme podle vztahu:
\[ R\,=\,\frac{1}{\sigma}\frac{l}{S}\,, \]kde l je délka vodiče a S jeho průřez (plocha).
Plocha jedné válcové slupky je rovna 2πrL. „Délku“ slupky označíme dr. Odpor dR jedné válcové slupky tedy vypočítáme pomocí vztahu:
\[ \mathrm{d}R\,=\,\frac{1}{\sigma\left(r\right)}\,\frac{l}{S}\,=\, \frac{r}{c}\,\frac{\mathrm{d}r}{2\pi rL} \] \[ \mathrm{d}R\,=\,\frac{\mathrm{d}r}{2\pi c L}\,. \]Válcové slupky jsou zapojeny sériově. Celkový odpor R materiálu mezi válcovými elektrodami tedy získáme součtem (integrací) odporů jednotlivých válcových slupek dR:
\[ R\,=\,\int_\mathrm{a}^\mathrm{b}\frac{\mathrm{d}r}{2\pi c L} \] \[ R\,=\,\frac{b\,-\,a}{2\pi c L}\,. \]II. Nápověda
Zkuste si nejprve vyřešit jednodušší úlohu Elektrický proud mezi válcovými elektrodami, a to II. způsobem, tj. s využitím Ohmova zákona v diferenciálním tvaru.
II. Rozbor
Prostor mezi válcovými elektrodami si rozdělíme na tenké válcové proužky o poloměru r, kde a < r < b.


Z válcové symetrie situace vyplývá, že ve všech místech takové slupky je stejná hustota proudu, kterou můžeme vyjádřit pomocí celkového proudu a plochy slupky. Celkový proud mezi elektrodami je stálý, nezávislý na poloměru r.
Ohmův zákon pro homogenní vodiče v diferenciálním tvaru říká, že hustota proudu procházejícího vodičem se rovná součinu měrné elektrické vodivosti a intenzity elektrického pole vodiče. Z tohoto zákona si vyjádříme intenzitu elektrického pole.
Napětí mezi elektrodami získáme integrací intenzity elektrického pole. Celkový odpor materiálu pak určíme jako podíl napětí mezi elektrodami a proudu, který mezi elektrodami prochází.
II. Řešení
Pokud mezi elektrodami prochází stálý proud I, pak z válcové symetrie situace vyplývá, že v tenkém válcovém proužku o poloměru r, kde a < r < b, je v každém místě stejná hustota proudu j(r) (protože plocha proužku závisí na jeho poloměru r, bude na poloměru záviset i hustota proudu). Celkový proud v tomto pásku tedy vypočítáme:
\[ I\,=\,j\left(r\right)\cdot S\,=\,j\left(r\right)\cdot 2\pi rL. \]Z tohoto vzorce si vyjádříme hustotu proudu j(r):
\[ j\left(r\right)\,=\,\frac{I}{2\pi rL}\,. \]Z diferenciálního tvaru Ohmova zákona
\[ \vec{j\,}\,=\,\sigma\vec{E}, \]kde \(\vec{j\,}\) je hustota elektrického proudu, \(\sigma\,=\,\frac{c}{r}\) měrná elektrická vodivost a \(\vec{E}\) intenzita elektrického pole, určíme velikost intenzity elektrického pole na povrchu tohoto pásku:
\[ E\left(r\right)\,=\,\frac{j\left(r\right)}{\sigma\left(r\right)}\,=\,\frac{I}{2\pi\sigma\left(r\right)rL}\,=\,\frac{I}{2\pi\frac{c}{r}rL}\,=\,\frac{I}{2\pi\sigma cL}\,. \]Napětí U mezi elektrodami získáme integrací intenzity elektrického pole:
\[ U\,=\,\int_\mathrm{a}^\mathrm{b} \vec{E}\left(r\right)\cdot \mathrm{d}\vec{r\,}. \]Díky válcové symetrii úlohy bude intenzita elektrického pole mířit v každém bodě vodiče radiálním směrem. Vektory \(\vec{E}\) a \(\mathrm{d}\vec{r\,}\) jsou tedy rovnoběžné a jejich skalární součin je proto roven součinu jejich velikostí:
\[ U\,=\,\int_\mathrm{a}^\mathrm{b} E\left(r\right)\,\mathrm{d}r\,=\,\frac{I}{2\pi cL}\int_\mathrm{a}^\mathrm{b} \mathrm{d}r\,=\,\frac{I}{2\pi cL}\left(b\,-\,a\right). \]Odpor materiálu získáme jako podíl napětí U mezi elektrodami a proudu I, který mezi elektrodami prochází:
\[ R\,=\,\frac{U}{I}\,=\,\frac{\frac{I}{2\pi cL}\left(b\,-\,a\right)}{I}\,=\,\frac{b\,-\,a}{2\pi cL}\,. \]Odpověď
Celkový odpor materiálu mezi elektrodami vypočítáme ze vztahu
\[ R\,=\,\frac{b\,-\,a}{2\pi cL}\,. \]Odkaz na podobnou úlohu
Zkuste si vyřešit také jednodušší úlohu Elektrický proud mezi válcovými elektrodami.



