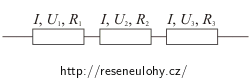Řešení obvodu s rezistory
Úloha číslo: 181
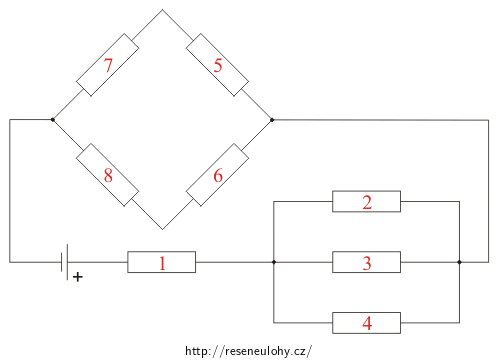
U všech rezistorů v obvodu na obrázku určete úbytek napětí a proud, který jimi protéká.
Odpor každého rezistoru je 3 Ω a elektromotorické napětí zdroje je 7 V. Vnitřní odpor zdroje neuvažujte.
Nápověda
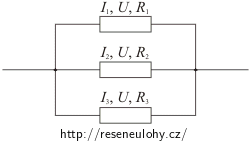
Uvědomte si, co platí pro celkové napětí, proud a odpor při sériovém a při paralelním zapojení.
Rozbor
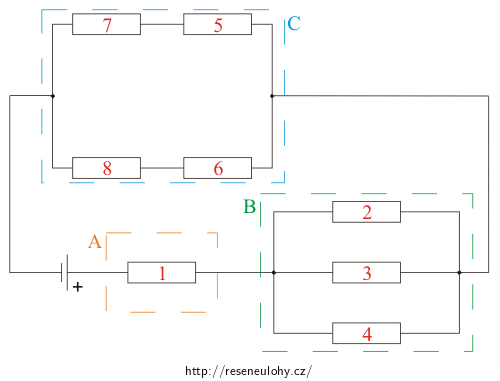
Abychom mohli proudy a napětí na všech rezistorech lépe spočítat, obvod si překreslíme a rozdělíme jej na tři části A, B, C, které jsou vzájemně připojeny sériově:
Pro každou část si vyjádříme celkový odpor. Díky tomu pak vypočítáme celkový proud procházející obvodem. Ten je podle Ohmova zákona roven podílu napětí na zdroji a celkového odporu obvodu.
Z celkového proudu pak určíme proudy procházející jednotlivými rezistory a dopočítáme úbytky napětí na rezistorech.
Obrázek k řešení úlohy
Obvod ze zadání úlohy si překreslíme a rozdělíme na tři části A, B, C:

1. část řešení - celkový proud procházející obvodem
Abychom mohli vypočítat proudy a napětí na rezistorech, musíme si nejprve vyjádřit celkový proud procházející obvodem.
Z Ohmova zákona víme, že pro celkový proud I, který prochází obvodem, platí:
\[I\,=\,\frac{U}{R_\mathrm{celk}}\,,\tag{*}\]kde U je napětí na zdroji a Rcelk je celkový odpor obvodu. Ten vypočítáme jako součet odporů částí A, B, C (viz Obrázek k řešení úlohy):
\[R_\mathrm{celk}\,=\,R_\mathrm{A}+R_\mathrm{B}+R_\mathrm{C}\,.\]Odpor RA je tvořen jen jedním rezistorem, a tedy:
\[R_\mathrm{A}\,=\,R\,,\]kde R je odpor rezistoru.
Část B je tvořena třemi paralelně zapojenými rezistory o odporu R:
\[\frac{1}{R_\mathrm{B}}\,=\,\frac{1}{R}+\frac{1}{R}+\frac{1}{R}\,=\,\frac{3}{R}\hspace{10px} \Rightarrow\hspace{10px}R_\mathrm{B}\,=\,\frac{R}{3}\,.\]Celkový odpor části C vypočítáme jako odpor dvou paralelních větví, na nichž jsou dva sériově zapojené rezistory:
\[\frac{1}{R_\mathrm{C}}\,=\,\frac{1}{2R}+\frac{1}{2R}\,=\,\frac{1}{R} \hspace{10px}\Rightarrow\hspace{10px}R_\mathrm{C}\,=\,R\,.\]Pro celkový odpor obvodu tedy platí:
\[R_\mathrm{celk}\,=\,R_\mathrm{A}+R_\mathrm{B}+R_\mathrm{C}\,=\,R+\frac{R}{3}+R\] \[R_\mathrm{celk}\,=\,\frac{7}{3}R\,.\]Takto vyjádřený celkový odpor dosadíme do rovnice (*)
\[I\,=\,\frac{U}{\frac{7}{3}R}\]a tím získáme celkový proud procházející obvodem:
\[I\,=\,\frac{3}{7}\,\frac{U}{R}\,.\]Ze zadání úlohy známe napětí na zdroji U a odpor každého rezistoru R:
\[U\,=\,7\,\mathrm{V}\] \[R\,=\,3\,\mathrm{\Omega}\,.\]Hodnota celkového proudu, který protéká obvodem je tedy:
\[I\,=\,1\,\mathrm{A}\,.\]2. část řešení - vyjádření a výpočet proudů
Připomeňme si, co platí pro proud v sériovém a paralelním zapojení:
1. Při sériovém zapojení je celkový proud procházející obvodem roven proudům procházejícím jednotlivými spotřebiči.
2. Při paralelním zapojení platí, že součet proudů procházejících jednotlivými spotřebiči se rovná celkovému proudu.
Díky těmto dvěma podmínkám si vyjádříme proudy procházející jednotlivými rezistory v obvodu v závislosti na celkovém proudu.
Protože jsou části A, B, C zapojeny sériově, z první podmínky vyplývá (viz Obrázek k řešení úlohy):
\[I\,=\,I_\mathrm{A}\,=\,I_\mathrm{B}\,=\,I_\mathrm{C}\,,\]kde I je celkový proud procházející obvodem a IA, B, C jsou proudy procházející jednotlivými částmi obvodu.
Proud procházející rezistorem 1:
\[I_1\,=\,I_\mathrm{A}\,=\,I\,.\]Paralelní větve v části B mají stejný odpor, proto se celkový proud rozdělí do těchto tří větví rovnoměrně:
\[I_2\,=\,I_3\,=\,I_4\,=\,\frac{I_\mathrm{B}}{3}\,=\,\frac{I}{3}\,.\]Podobně je tomu i u části C. Díky symetrii obvodu se proud vstupující do části C rozdělí na dvě poloviny:
\[I_5\,=\,I_6\,=\,\frac{I}{2}\,.\]To samé platí i pro rezistory 7 a 8. Velikosti proudů procházejících těmito rezistory jsou stejné a jejich součet se musí opět rovnat velikosti celkového proudu. Tedy:
\[I_7\,=\,I_8\,=\,\frac{I}{2}\,.\]V předchozím oddíle jsme si vypočítali hodnotu celkového proud I, který protéká obvodem:
\[I\,=\,1\,\mathrm{A}\,.\]Pro proudy procházející jednotlivými rezistory tedy platí:
\[I_1\,=\,I\,=\,1\,\mathrm{A}\] \[I_2\,=\,I_3\,=\,I_4\,=\,\frac{I}{3}\,=\,\frac{1}{3}\,\mathrm{A}\] \[I_5\,=\,I_6\,=\,I_7\,=\,I_8\,=\,\frac{I}{2}\,=\,\frac{1}{2}\,\mathrm{A}\,.\]3. část řešení - vyjádření a výpočet úbytků napětí
Pro napětí v sériovém a paralelním zapojení platí:
1. Při sériovém zapojení je celkové napětí obvodu rovno součtu napětí na jednotlivých spotřebičích.
2. Při paralelním zapojení platí, že celkové napětí se rovná napětí na každé větvi.
Za pomoci těchto podmínek a Ohmova zákona (U = RI) si vyjádříme napětí na všech rezistorech.
Vzhledem k tomu, že jsou části A, B, C zapojeny sériově, tak z první podmínky vyplývá:
\[U\,=\,U_\mathrm{A}+U_\mathrm{B}+U_\mathrm{C}\,,\]kde U je celkové napětí obvodu a UA,B,C jsou napětí na jednotlivých částech obvodu (viz Obrázek k řešení úlohy).
Napětí na prvním rezistoru:
\[U_\mathrm{A}\,=\,U_1\,=\,RI_1\,.\]Protože větve v části B mají stejný odpor, bude podle druhé podmínky na všech větví stejné napětí UB:
\[U_\mathrm{B}\,=\,U_2\,=\,U_3\,=\,U_4\,=\,RI_2\,.\]V části C je opět na obou paralelních větvích stejné napětí:
\[U_5+U_7\,=\,U_6+U_8\,.\]Protože všechny rezistory mají stejný odpor, platí navíc, že:
\[U_5\,=\,U_7\] \[U_6\,=\,U_8\,.\]A tedy:
\[U_5\,=\,U_6\,=\,U_7\,=\,U_8\,=\,RI_5\,.\]V předchozím oddíle jsme si vypočítali proudy na jednotlivých rezistorech:
\[I_1\,=\,1\,\mathrm{A}\] \[I_2\,=\,I_3\,=\,I_4\,=\,\frac{1}{3}\,\mathrm{A}\] \[I_5\,=\,I_6\,=\,I_7\,=\,I_8\,=\,\frac{1}{2}\,\mathrm{A}\,.\]Ze zadání úlohy víme, že odpor každého rezistoru v obvodu R je 3 Ω.
Nyní můžeme dopočítat úbytky napětí na rezistorech:
\[U_1\,=\,RI_1\,=\,3\,\mathrm{V}\] \[U_2\,=\,U_3\,=\,U_4\,=\,RI_2\,=\,1\,\mathrm{V}\] \[U_5\,=\,U_6\,=\,U_7\,=\,U_8\,=\,RI_5\,=\,\frac{3}{2}\,\mathrm{V}\,.\]Tabulka s výsledky
Proudy procházející jednotlivými rezistory, jejichž odpor je 3 Ω, a úbytky napětí na těchto rezistorech jsou zaznamenány v tabulce:
číslo rezistoru: 1 2 3 4 5 6 7 8 proud: 1 A 1/3 A 1/3 A 1/3 A 1/2 A 1/2 A 1/2 A 1/2 A napětí: 3 V 1 V 1 V 1 V 3/2 V 3/2 V 3/2 V 3/2 V