Paralelní zapojení reálných zdrojů
Úloha číslo: 2149
Určete elektromotorické napětí \(U_\mathrm{e,v}\) a vnitřní odpor \(R_\mathrm{i,v}\) zdroje, kterým bychom ekvivalentně nahradili zapojení n stejných paralelně zapojených baterií s parametry \(U_\mathrm{e}\) a \(R_\mathrm{i}\). Úlohu řešte metodou lineární superpozice.
Odkaz – metoda lineární superpozice
O tom, co je linearní superpozice a jak ji lze použít na příklady tohoto typu, se můžete dočíst na odkazu Metoda lineární superpozice.
Rozbor
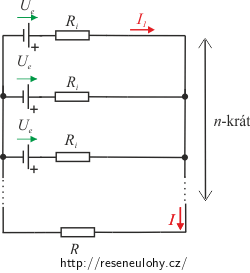
Metodou lineární superpozice vyjádříme proud I procházející rezistorem o odporu R. Výsledný vztah poté srovnáme s Ohmovým zákonem pro uzavřený obvod a odsud určíme hledané elektromotorické napětí a vnitřní odpor náhradního zdroje.
Stručně o metodě lineární superpozice:
Metodu lineární superpozice používáme v obvodech, ve kterých působí více zdrojů elektrické energie. Proud na vybraném prvku se určí tak, že necháme v obvodu zapojený jen jeden zdroj napětí a ostatní zdroje napětí nahradíme jejich vnitřním odporem. Stanovíme proud na uvažovaném prvku v takto upraveném obvodu. Toto provedeme postupně pro každý zdroj. Výsledný proud na uvažovaném prvku je potom součet proudů vyvolaných jednotlivými zdroji samostatně.
Řešení
Úlohu řešíme metodou lineární superpozice. Necháme první zdroj napětí, ostatní zdroje nahradíme jejich vnitřními odpory a vyjádříme proud procházející rezistorem o odporu R.
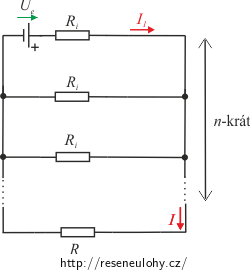
Nejprve vyjádříme celkový odpor zapojení. V obvodu je \((n-1)\) paralelně zapojených rezistorů s odporem \(R_\mathrm{i}\) k nim je paralelně zapojen rezistor o odporu R a tato soustava rezistorů je v sérii s odporem \(R_\mathrm{i}\).
Celkový odpor \((n-1)\) paralelně zapojených rezistorů s odporem \(R_\mathrm{i}\) se spočítá jako
\[\frac{1}{R_\mathrm{v1}}=\frac {1}{R_\mathrm{i}} + ... + \frac {1}{R_\mathrm{i}}= \frac {n-1}{R_\mathrm{i}},\] \[{R_\mathrm{v1}}=\frac {R_\mathrm{i}} {n-1}.\]Připojíme-li paralelně k tomuto rezistoru rezistor o odporu R, výsledný odpor bude
\[\frac {1}{R_\mathrm{v2}}=\frac {1}{\frac {R_\mathrm{i}} {n-1}} + \frac {1}{R}, \] \[R_\mathrm{v2}=\frac {R_\mathrm{i} R} {(n-1)R + R_\mathrm{i}}.\]Tento výsledný odpor je v sérii s vnitřním odporem zdroje, celkový odpor zapojení:
\[R_\mathrm{c}=R_\mathrm{i} + \frac {R_\mathrm{i} R} {(n-1)R + R_\mathrm{i}}.\]Z Ohmova zákona vyjádříme proud \(I_1\), což je proud, který prochází obvodem na obrázku:
\[I_1 = \frac {U_\mathrm{e}}{R_\mathrm{i} + \frac {R_\mathrm{i} R} {(n-1)R + R_\mathrm{i}}} = \frac {U_\mathrm{e}[(n-1)R+R_\mathrm{i}]}{R_\mathrm{i}^2 +(n-1)RR_\mathrm{i} + R_\mathrm{i}R}=\frac {U_\mathrm{e}[(n-1)R+R_\mathrm{i}]}{R_\mathrm{i}^2 +nRR_\mathrm{i}},\]který se rozdělí do jednotlivých větví paralelního zapojení \((n-1)\) rezistorů s odporem \(R_\mathrm{i}\) a rezistoru s odporem \(R\). Při výpočtu proudu \(I_\mathrm{R1}\) rezistorem s odporem \(R\) využijeme toho, že v paralelním zapojení se proud rozdělí v obráceném poměru k odporům
\[\frac{I_\mathrm{R1}}{I_1} = \frac{R_\mathrm{v2}}{R},\]odkud vyjádříme
\[I_\mathrm{R1} = \frac{U_\mathrm{e}[(n-1)R+R_\mathrm{i}]}{R_\mathrm{i}^2 +nRR_\mathrm{i}} \frac{\frac{R_\mathrm{i} R}{(n-1)R + R_\mathrm{i}}}{R} = \frac{U_\mathrm{e}}{R_\mathrm{i} +nR}. \]Jelikož máme v zadaném obvodu stejné zdroje, příspěvek k proudu rezistorem \(R\) od každého zdroje bude stejný. Proud procházející rezistorem \(R\) bude
\[I=nI_\mathrm{R1} =\frac{n U_\mathrm{e} }{R_\mathrm{i} +nR}. \]Ohmův zákon pro uzavřený obvod má obecně tvar
\[I=\frac{U_\mathrm{e}}{R_\mathrm{i} + R}.\]Proud procházející rezistorem o odporu R upravíme do tvaru Ohmova zákona pro uzavřený obvod:
\[I=\frac{nU_\mathrm{e}}{R_\mathrm{i} + nR}=\frac{U_\mathrm{e}}{\frac{R_\mathrm{i}}{n} +R}.\]Porovnáním s Ohmovým zákonem pro uzavřený obvod, získáme
\[U_\mathrm{e,v} = U_\mathrm{e}.\] \[R_\mathrm{i,v} = \frac {R_\mathrm{i}}{n}.\]K čemu je to dobré?
Paralelní zapojení zdrojů nám zmenší vliv vnitřního odporu a zvýší dodávaný proud.
Odpověď
Elektromotorické napětí zdroje, kterým bychom nahradili n paralelně zapojených zdrojů, je \( U_\mathrm{e,v} = U_\mathrm{e}\) a odpor tohoto zdroje je \(R_\mathrm{i,v} = \frac {R_\mathrm{i}}{n}.\)

