Elektromotorické napětí způsobené časově se měnícím magnetickým polem
Úloha číslo: 2331
Homogenní magnetické pole \(B\) je kolmé na kruhovou smyčku zanedbatelného odporu a míří ve směru osy z (směrem z obrázku k nám). Velikost magnetické indukce se postupně mění podle zadaného grafu. Smyčka má poloměr \(r = 50\thinspace\mathrm{cm}\) a je spojena s rezistorem o odporu \(R=2 \space \Omega\). Kladný směr (proti směru chodu hodinových ručiček) je znázorněn na obrázku.
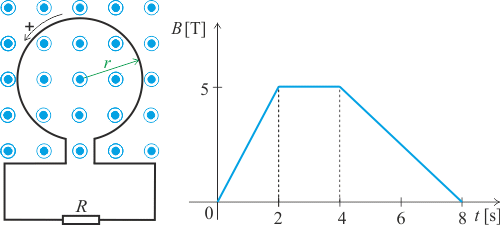
(a) Vyjádřete časový průběh indukovaného elektromotorického napětí \(U_\mathrm{i}\) v obvodu v intervalu, na kterém je zadané \(B\).
(b) Nakreslete graf závislosti indukovaného elektromotorického napětí \(U_\mathrm{i}\) na čase (i s hodnotami na osách včetně jednotek).
(c) Nakreslete závislost proudu \(I\) rezistorem \(R\) na čase.
(d) Nakreslete závislost výkonu \(P\) na rezistoru \(R\) na čase.
Nápověda
Faradayův zákon elektromagnetické indukce říká: Změní-li se magnetický indukční tok plochou vodivé smyčky za dobu \(\Delta t\) o \(\Delta\Phi\), vzniká ve smyčce indukované elektromotorické napětí, jež je dáno vztahem
\[U_\mathrm{i} = - \frac{\Delta\Phi}{\Delta t}.\]Magnetický indukční tok plochou o obsahu S je v případě homogenního pole definován jako \(\Phi=BS\cos\alpha\), kde \(\alpha\) je úhel, který svírá normála plochy s vektorem magnetické indukce \(\vec{B}.\)
K určení směru proudu indukovaného v cívce nám pomůže Lenzův zákon. Ten nám říká, že indukovaný proud má takový směr, aby svým magnetickým polem působil proti změně magnetického indukčního toku, která je jeho příčinou.
Řešení
(a) Vyjádření indukovaného napětí
K řešení využijeme Faradayův zákon elektromagnetické indukce, který pro homogenní pole a rovinnou smyčku má tvar
\[U_\mathrm{i}=-\frac{\mathrm{d}\Phi}{\mathrm{d} t}=-\frac{\mathrm{d} BS\cos\alpha}{\mathrm{d} t}.\]Jelikož normála plochy smyčky a vektor magnetické indukce jsou rovnoběžné, platí pro úhel \(\alpha=0°\), tj. \(\cos\alpha=1\). Obsah plochy smyčky se s časem nemění a je roven obsahu kruhu \(S=\pi r^2\). Dostáváme
\[U_\mathrm{i}=-\pi r^2\frac{\mathrm{d} B}{\mathrm{d} t}.\]Jelikož je časový průběh velikosti magnetického pole po částech lineární (skládá se z lineárních částí), můžeme derivaci přepsat jako podíl \(\Delta B\) a \(\Delta t\). Pokud by průběh byl nelineární, pak by takové zjednodušení nebylo možné:
\[U_\mathrm{i}=-\pi r^2\frac{\Delta B}{\Delta t}.\]Dosazením určíme indukované napětí pro jednotlivé lineární části grafu:
- \(t_1=0\space \mathrm{s},\space t_2=2\space \mathrm{s},\space B_1=0\space \mathrm{T},\space B_2=5\space \mathrm{T}\) \[U_\mathrm{i1}=-\pi r^2\frac{\Delta B}{\Delta t}=-\pi r^2\frac{B_2-B_1}{t_2-t_1}=-\pi\cdot 0{,}5^2\cdot\frac{5 - 0}{2 - 0}\space \mathrm{V}=-1{,}96 \space \mathrm{V},\]
- \(t_2=2\space \mathrm{s},\space t_3=4\space \mathrm{s},\space B_2=5\space \mathrm{T},\space B_3=5\space \mathrm{T}\) \[U_\mathrm{i2}=-\pi\cdot 0{,}5^2\cdot\frac{5-5}{4-2}\space \mathrm{V}=0\space \mathrm{V},\]
- \(t_3=4\space \mathrm{s},\space t_4=8\space \mathrm{s},\space B_3=5\space \mathrm{T},\space B_4=0\space \mathrm{T}\) \[U_\mathrm{i3}=-\pi\cdot 0{,}5^2\cdot\frac{0-5}{8-4}\space \mathrm{V}=0{,}98\space \mathrm{V}.\]
Indukované napětí v první části \(U_\mathrm{i1}\) vyšlo záporné, což znamená, že indukovaný proud poteče proti kladnému směru (tj. poteče ve směru hodinových ručiček). Smyčka bude vytvářet magnetické pole vstupující do obrázku (dle Ampérova pravidla pravé ruky), a tedy působící proti magnetickému poli, které indukované napětí způsobilo. To je přesně v souladu s Lenzovým zákonem. Analogickou úvahu můžeme provést v případě \(U_\mathrm{i3}.\) Indukované napětí v druhé části \(U_\mathrm{i2}\) je nulové, což odpovídá tomu, že se v tomto časovém intervalu magnetická indukce ani magnetický tok nemění.
(b) Graf závislosti indukovaného napětí na čase
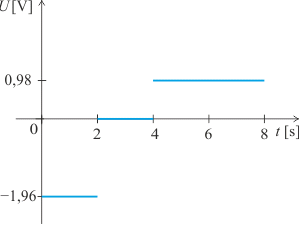
(c) Závislost proudu procházejícího rezistorem
Pro nakreslení závislosti proudu rezistorem na čase si nejprve vypočítáme z Ohmova zákona proudy v jednotlivých časových úsecích:
- V časech mezi \(t_1=0\space \mathrm{s},\space t_2=2\space \mathrm{s}\) \[I=\frac{U}{R}=\frac{-1{,}96}{2}\thinspace \Omega=-0{,}98 \thinspace \mathrm{A},\]
- V časech mezi \(t_2=2\space \mathrm{s},\space t_3=4\space \mathrm{s}\) \[I=\frac{U}{R}=\frac{0}{2}\thinspace \Omega=0 \thinspace \mathrm{A},\]
- V časech mezi \(t_3=4\space \mathrm{s},\space t_4=8\space \mathrm{s}\) \[I=\frac{U}{R}=\frac{0{,}98}{2}\thinspace \Omega=0{,}49 \thinspace \mathrm{A}.\]
Směr proudu (vyjádřený jeho znaménkem) je stejný jako směr napětí, a proto je v prvním časovém intervalu proud záporný a v posledním časovém intervalu proud kladný.
Graf závislosti indukovaného proudu
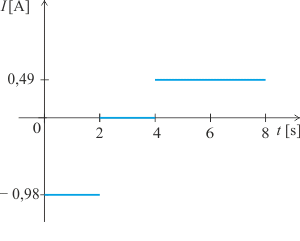
(d) Závislost výkonu na rezistoru
Výkon na rezistoru o odporu \(R\), kterým prochází proud \(I\), vypočteme pomocí vztahu
\[P=UI.\]- V časech mezi \(t_1=0\space \mathrm{s},\space t_2=2\space \mathrm{s}\) \[P=UI=(-1{,}96) \cdot (-0{,}98) \space \mathrm{W}=1{,}92 \space \mathrm{W},\]
- V časech mezi \(t_2=2\space \mathrm{s},\space t_3=4\space \mathrm{s}\) \[P=UI=0{\cdot} 0 \space \mathrm{W}=0 \space \mathrm{W},\]
- V časech mezi \(t_3=4\space \mathrm{s},\space t_4=8\space \mathrm{s}\) \[P=UI=0{,}98{\cdot} 0{,}49 \space \mathrm{W}=0{,}48 \space \mathrm{W}.\]
Výkon na rezistoru bude vždy nezáporný, jelikož rezistor energii spotřebovává (mění na teplo).
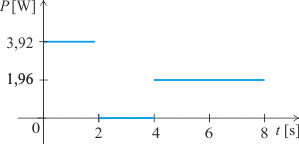
Odpověď — přehled grafů
Graf závislosti indukovaného napětí na čase

Graf závislosti indukovaného proudu na čase
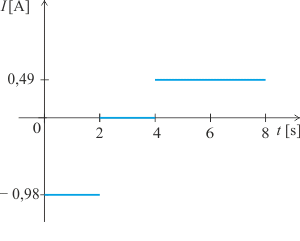
Závislost výkonu na rezistoru na čase


