Sbírka řešených úloh

Zavěšené nabité kuličky

Úloha číslo: 8

• Nápověda

  Jaké síly na kuličky působí a jaký je jejich směr? Zkuste si nakreslit obrázek.

• Rozbor

  Na každou kuličku zavěšenou na vlákně působí tíhová síla a tahová síla vlákna. Naše kuličky jsou navíc nabité, takže se budou vzájemně odpuzovat elektrickou silou. Její velikost získáme pomocí Coulombova zákona.

  Obě kuličky jsou v klidu, proto výslednice všech tří sil musí být nulová. Aby výslednice byla nulová, musí být výslednice elektrické a tíhové síly stejně velká a mít opačný směr než tahová síla lanka. Na obrázku můžeme najít dva podobné trojúhelníky („zelený“ a „fialový“). Z podobnosti obou trojúhelníků vyjádříme neznámou velikost elektrické síly a z ní náboj kuliček.

  

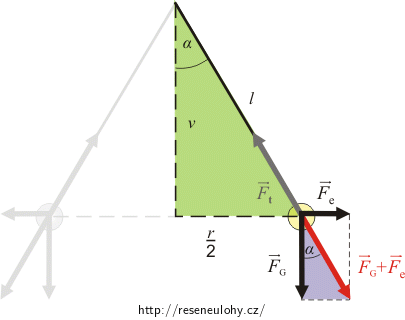
• Obrázek působících sil

  

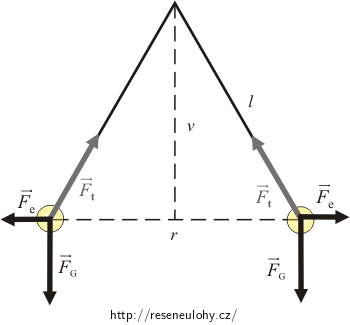
• Řešení

  Na každou kuličku zavěšenou na vlákně působí tíhová síla \( \vec{F}_\mathrm{G}\) a tahová síla vlákna \( \vec{F}_\mathrm{t}\). Protože jsou kuličky nabité stejným nábojem, působí na ně navíc odpudivá elektrická síla \( \vec{F}_\mathrm{e}\).

  Velikost elektrické odpudivé síly určíme z Coulombova zákona:

  \[F_\mathrm{e} \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q_1 Q_2}{r^2}\,.\]

  Obě kuličky jsou nabity stejně velkým nábojem Q, proto můžeme zápis zjednodušit:

  \[F_\mathrm{e} \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q^2}{r^2}\,.\]

  Vzhledem k tomu, že jsou kuličky v klidu, je výslednice všech tří sil působících na kuličku rovna nule.

  Síla \(\vec{F}_\mathrm{e}+\vec{F}_\mathrm{G}\) musí působit proti tahové síle vlákna \(\vec{F}_\mathrm{t}\). Díky tomu jsou „zeleně“ a „fialově“ označené trojúhelníky podobné. Z „fialového“ trojúhelníka si vyjádříme tg α:

  \[\mathrm{tg}\,\alpha\,=\,\frac{F_\mathrm{e}}{F_\mathrm{G}}\,=\,\frac{\frac{1}{4\pi\varepsilon_0}\,\frac{Q^2}{r^2}}{mg}\,=\,\frac{Q^2}{4 \pi\varepsilon_0mgr^2}.\]

  Úhel α nalezneme také v podobném „zeleném“ trojúhelníku. Opět si vyjádříme tangens tohoto úhlu:

  \[\mathrm{tg}\,\alpha\,=\,\frac{\frac{r}{2}}{v}\,=\,\frac{r}{2v}.\]

  Stranu v „zeleného“ trojúhelníka spočítáme pomocí Pythagorovy věty \(v\,=\,\sqrt{ l^2-\left(\frac{r}{2}\right)^2}\) a dosadíme:

  \[\mathrm{tg}\,\alpha\,=\,\frac{r}{2 \sqrt{ l^2-(\frac{r}{2})^2} }\,=\,\frac{r}{ \sqrt{ 4l^2-r^2} }.\]

  Nyní oba vztahy pro tangens úhlu α porovnáme:

  \[\frac{Q^2}{4 \pi \varepsilon_0 mgr^2}\,=\,\frac{r}{\sqrt{ 4l^2-r^2} } \]

  a vyjádříme z nich neznámý náboj Q:

  \[Q^2\,=\,\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} } ,\] \[Q\,=\,\sqrt{\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} } }.\]

• Zápis a číselné dosazení:

  \(m\,=\,0{,}5\,\mathrm{g}\,=\,5{\cdot} 10^{-4}\,\mathrm{kg}\)	hmotnost kuliček
  \(l\,=\,1\,\mathrm{m}\)	délka vláken
  \(r\,=\,4\,\mathrm{cm}\,=\,4{\cdot} 10^{-2}\,\mathrm{m}\)	vzdálenost kuliček
  \(Q\,=\,?\,\left(\mathrm{C}\right)\)
  Konstanty vyhledané v tabulkách:
  \(\varepsilon_0\,=\,8{,}85{\cdot} 10^{-12}\,\mathrm{ C^2\,N^{-1}\,m^{-2}}\)
  \(g\,=\,9{,}8\,\mathrm{ m\,s^{-2}}\)

  ---

  \[\begin{eqnarray} Q\,&=&\,\sqrt{\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} } }\\ Q\,&=&\,\sqrt{\frac{4\pi \,\cdot\,8{,}85{\cdot} 10^{-12}\, \cdot \,5{\cdot} 10^{-4}\, \cdot\,9{,}8 \,\cdot\, \left(4 {\cdot}10^{-2}\right)^3}{ \sqrt{ 4 {\cdot} 1^2-\left(4 {\cdot}10^{-2}\right)^2}}}\,\mathrm{C}\\ Q\,&\dot=&\,4{,}2{\cdot}10^{-9}\,\mathrm{C}\,\dot=\,4{,}2\,\mathrm{nC} \end{eqnarray}\]

• Odpověď

  Každá kulička byla nabita nábojem \(Q\,=\,\sqrt{\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} }} \,\dot=\,4{,}2\,\mathrm{nC} \).

• Odkaz na obtížnější úlohu

  Úloha, ve které jsou kuličky navíc ponořeny do benzenu, má název Kuličky na niti ponořené do benzenu.