Elektrický proud mezi válcovými elektrodami

Úloha číslo: 320

Dvě válcové elektrody o délce L a o poloměrech a a b, kde b > a, jsou odděleny homogenním materiálem o vodivosti σ. Mezi elektrodami je napětí U. Jaký je elektrický odpor mezi elektrodami? Jaký proud prochází v prostoru mezi elektrodami?

Poznámka: Tuto úlohu zde řešíme třemi způsoby:

I. přímou integrací odporů jednotlivých částí vodiče,

II. s využitím Ohmova zákona (v diferenciálním tvaru),

III. pomocí formální podobnosti se zákony elektrostatiky.

I. Nápovědy
Nápověda 1
Celý vodič si rozdělte na tenké válcové proužky o poloměru r, kde a < r < b.

Celý vodič je sériovým zapojením těchto slupek. Celkový odpor vodiče tedy bude roven součtu odporů jednotlivých slupek.
Nápověda 2
Uvědomte si nebo vyhledejte, jak závisí elektrický odpor na rozměrech a vodivosti materiálu.
Řešení nápovědy 2
Elektrický odpor homogenního vodiče R je nepřímo úměrný vodivosti materiálu σ. Velikost elektrického odporu vypočítáme podle vztahu:
\[R\,=\,\frac{1}{\sigma}\,\frac{l}{S}\,,\]
kde l je délka vodiče a S je obsah jeho průřezu („tloušťka“).

Celý vodič jsme si rozdělili na tenké válcové slupky o poloměru r. „Plocha“ každé válcové slupky je rovna 2πrL a její „délku“ označíme dr. Každá válcová slupka má tedy odpor:
\[R_\mathrm{r}\,=\,\frac{1}{\sigma}\,\frac{\mathrm{d}r}{2\pi rL}\,.\]
I. Rozbor
Vodič si rozdělíme na tenké válcové slupky o poloměru r, kde a < r < b.

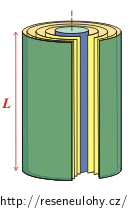
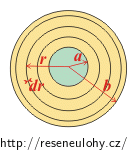
Celý vodič nyní můžeme brát jako sériové zapojení těchto slupek. Celkový odpor vodiče tedy získáme součtem (integrací) odporů jednotlivých slupek.

Elektrický odpor válcové slupky je přímo úměrný její „délce“ a nepřímo úměrný „ploše“ slupky a vodivosti materiálu.

Proud procházející mezi elektrodami se rovná podílu napětí a elektrického odporu mezi elektrodami.
I. Řešení
Válcový prostor mezi elektrodami si rozdělíme na tenké válcové slupky o poloměru r, kde a < r < b.

Celý vodič můžeme nyní považovat za sériové zapojení válcových slupek.

Elektrický odpor vodiče vypočítáme ze vztahu:
\[R\,=\,\frac{1}{\sigma}\,\frac{l}{S}\,,\]
kde σ je vodivost materiálu, l délka vodiče a S plocha jeho průřezu.

V našem případě se „plocha“ jedné slupky rovná 2πrL a délku slupky označíme dr. Odpor R_r válcové slupky pak vyjádříme vztahem:
\[ R_\mathrm{r}\,=\,\frac{1}{\sigma}\,\frac{\mathrm{d}r}{2\pi rL}\,. \]
Protože jsou válcové slupky zapojeny sériově, bude celkový odpor mezi válcovými elektrodami roven součtu (integraci) všech slupek R_r od poloměru a do poloměru b:
\[ R\,=\int_\mathrm{a}^\mathrm{b}\,\frac{1}{\sigma}\,\frac{\mathrm{d}r}{2\pi rL}\,=\, \frac{1}{2\pi \sigma L}\int_\mathrm{a}^\mathrm{b}\frac{\mathrm{d}r}{r}\,=\,\frac{1}{2\pi \sigma L}\left[\ln{r}\right]_\mathrm{a}^\mathrm{b}\,=\,\frac{1}{2\pi \sigma L}\,\left(\ln{b}-\ln{a}\right). \]
Celkový elektrický odpor mezi válcovými elektrodami tedy můžeme vypočítat pomocí vzorce:
\[ R\,=\,\frac{\ln{\frac{b}{a}}}{2\pi \sigma L}\,. \]
Proud I procházející mezi elektrodami se rovná podílu napětí U a elektrického odporu R mezi elektrodami:
\[ I\,=\,\frac{U}{R}\,=\, \frac{U}{\frac{\ln{\frac{b}{a}}}{2\pi \sigma L}}\,=\, \frac{2\pi \sigma L}{\ln{\frac{b}{a}}}\,U. \]
II. Nápovědy
Nápověda 1
Uvědomte si nebo vyhledejte, jak vypadá Ohmův zákon v diferenciálním tvaru.
Řešení nápovědy 1
Ohmův zákon pro homogenní vodiče v diferenciálním tvaru je dán vztahem:
\[\vec{j\,}=\,\sigma \vec{E},\]
kde \(\vec{j\,}\) je hustota elektrického proudu, σ měrná elektrická vodivost a \(\vec{E}\) značí intenzitu elektrického pole.
Nápověda 2
Uvědomte si, jak pomocí intenzity elektrického pole můžeme určit velikost napětí mezi elektrodami.

Celkový odpor potom bude podíl napětí mezi elektrodami a celkového proudu.
Řešení nápovědy 2
Elektrické pole vodiče o intenzitě \(\vec{E}\) vytváří mezi konci vodiče elektrické napětí U. Elektrické napětí U mezi dvěma místy je rovno rozdílu elektrických potenciálů těchto dvou míst.

Mezi elektrickou intenzitou \(\vec{E}\) a potenciálem \(\varphi\) v bodě P platí:
\[\varphi =-\int_0^\mathrm{P} \vec{E}\cdot\mathrm{d}\vec{r\,},\]
kde integrujeme z místa, kde jsme zvolili nulový potenciál, do místa P (integrál nezávisí na zvolené integrační cestě).

Odtud pro napětí mezi souosými válcovými elektrodami o poloměrech a, b (a < b) plyne:
\[U=\int_\mathrm{a}^\mathrm{b} \vec{E}\cdot\mathrm{d}\vec{r\,}.\]
II. Rozbor
Prostor mezi válcovými elektrodami si rozdělíme na tenké válcové proužky o poloměru r, kde a < r < b.

Z válcové symetrie situace vyplývá, že ve všech místech takové slupky je stejná hustota proudu, kterou můžeme vyjádřit pomocí celkového proudu a plochy slupky. Celkový proud mezi elektrodami je stálý, nezávislý na poloměru r.

Ohmův zákon pro homogenní vodiče v diferenciálním tvaru říká, že hustota proudu procházejícího vodičem se rovná součinu měrné elektrické vodivosti a intenzity elektrického pole vodiče. Z tohoto zákona si vyjádříme intenzitu elektrického pole.

Napětí mezi elektrodami získáme integrací intenzity elektrického pole. Celkový odpor materiálu pak určíme jako podíl napětí mezi elektrodami a proudu, který mezi elektrodami prochází.
II. Řešení
Prostor mezi elektrodami si rozdělíme na tenké válcové slupky o poloměru r, kde a < r < b. Z válcové symetrie situace vyplývá, že ve všech místech takové slupky je stejná hustota proudu j. Pro celkový proud procházející slupkou tedy platí:
\[ I=S\,j\left(r\right)=2\pi rL\,j\left(r\right). \tag{1}\]
Celkový proud mezi elektrodami je stálý a není tedy závislý na poloměru r.

Z diferenciálního tvaru Ohmova zákona pro homogenní vodič
\[ \vec{j\,}=\,\sigma\vec{E}\mathrm{,} \]
kde \(\vec{j\,}\) je hustota elektrického proudu, \(\sigma\) je měrná elektrická vodivost a \(\vec{E}\) intenzita elektrického pole, určíme velikost intenzity elektrického pole v dané válcové slupce o poloměru r:
\[ E\left(r\right)\,=\,\frac{j\left(r\right)}{\sigma}\,. \]
Hustotu proudu j(r) ve válcovém vodiči o poloměru r získáme ze vztahu (1) a dosadíme:
\[ E\left(r\right)\,=\,\frac{I}{2\pi\sigma rL}\,. \]
Napětí mezi elektrodami získáme integrací intenzity elektrického pole:
\[ U\,=\,\int_\mathrm{a}^\mathrm{b}\vec{E}\left(r\right)\cdot \mathrm{d}\vec{r\,}. \]
Protože vektory \(\vec{E}\left(r\right)\) a \(\mathrm{d}\vec{r\,}\) jsou rovnoběžné, je jejich skalární součin roven součinu jejich velikostí. Tedy:
\[ U\,=\,\int_\mathrm{a}^\mathrm{b}E\left(r\right)\,\mathrm{d}r. \]
Do této rovnice dosadíme za intenzitu a zintegrujeme:
\[ U\,=\,\int_\mathrm{a}^\mathrm{b}E\left(r\right)\,\mathrm{d}r\,=\,\int_\mathrm{a}^\mathrm{b}\frac{I}{2\pi\sigma rL}\,\mathrm{d}r\,=\,\frac{I}{2\pi\sigma L}\int_\mathrm{a}^\mathrm{b}\frac{1}{r}\,\mathrm{d}r\,=\,\frac{I}{2\pi\sigma L}\,\left[\ln{r}\right]_\mathrm{a}^\mathrm{b}\,=\,\frac{I}{2\pi\sigma L}\,\left(\ln{b}\,-\,\ln{a}\right). \]
Pro napětí mezi válcovými elektrodami tedy platí:
\[ U\,=\,\frac{I}{2\pi\sigma L}\,\ln{\frac{b}{a}}. \]
Elektrický odpor mezi elektrodami vypočítáme jako podíl napětí U mezi elektrodami a celkového proudu I, který mezi elektrodami prochází:
\[ R\,=\,\frac{U}{I}\,=\,\frac{\frac{I}{2\pi\sigma L}\,\ln{\frac{b}{a}}}{I} \] \[ R\,=\,\frac{\ln{\frac{b}{a}}}{2\pi\sigma L}\,. \]
Celkový proud procházející mezi elektrodami:
\[ I\,=\,\frac{U}{R}\,=\,\frac{2\pi\sigma L}{\ln{\frac{b}{a}}}\,U. \]
III. Nápovědy
Nápověda 1
Elektrické pole vytvořené mezi válcovými elektrodami je stacionární (časově neproměnné). Ve stacionární situaci můžeme použít formální podobnost se zákony elektrostatiky.
Vysvětlení formální podobnosti se zákony elektrostatiky
Ve stacionárním případě nezávisí žádná makroskopická veličina na čase. Může tedy existovat jen časově neproměnné rozložení nábojů v prostoru. Některé náboje jsou v klidu, jiné však konají makroskopický pohyb, a tak vytvářejí stacionární elektrický proud (jeho celková velikost i hustota je ale časově neproměnná).

Makroskopická rychlost nábojů realizujících proud je téměř vždy ve srovnání s rychlostí světla ve vakuu malá. Elektrické pole náboje, který se pohybuje takto pomalu, je popsáno vztahem, který je shodný s výrazem pro elektrické pole stojícího bodového náboje. Makroskopické stacionární elektrické pole, které představuje střední hodnotu pole pohybujících se nábojů, bude tedy časově neproměnné a bude vyhovovat všem základním rovnicím platným pro pole elektrostatické – proto v naší úloze využijeme např. platnost Gaussovy věty i pro stacionární případ.

Velký rozdíl mezi statickým a stacionárním elektrickým polem je v tom, že stacionární elektrické pole může být trvale nenulové i uvnitř vodičů (ve kterých teče proud). Úlohy o elektrostatickém a stacionárním elektrickém poli jsou tedy popsány formálně shodnými rovnicemi, liší se pouze v okrajových podmínkách.
Nápověda 2
Vyhledejte si formulaci Gaussovy věty elektrostatiky v integrálním tvaru.
Řešení nápovědy 2
Gaussovu větu vyjádříme v integrálním tvaru jako:
\[ \oint \vec{E}\cdot \mathrm{d}\vec{S}\,=\,\frac{Q}{\epsilon}\,, \]
kde značka \(\normalsize{\oint}\) vyjadřuje, že plošný integrál je brán přes uzavřenou plochu, \(\vec{E}\) je intenzita elektrického pole, Q celkový náboj uzavřený uvnitř plochy S a ε je permitivita dané látky.

Gaussova věta nám dává vztah mezi intenzitou elektrického pole a nábojem.
Nápověda 3
Pokud by mezi elektrodami nebyl vodič ale dielektrikum, jednalo by se vlastně o kondenzátor. Nicméně díky formální podobnosti se zákony elektrostatiky popsané v Nápovědě 1 bude průběh intenzity elektrického pole úplně stejný. Elektrickou intenzitu v Gaussově větě tedy sice vyjádříme ve stacionárním případě, ale pro náboj Q si „půjčíme“ vztah ze statického případu.

Velikost náboje tedy vyjádříme pomocí kapacity válcových elektrod. Takto vyjádřenou velikost náboje dosadíme do Gaussovy věty elektrostatiky.
Řešení nápovědy 3
Protože při výpočtu této úlohy lze využít formální podobnosti se zákony elektrostatiky, „vypůjčíme“ si velikost náboje ze statického případu:

Vztah mezi velikostí náboje Q a rozdílem potenciálů U lze vyjádřit pomocí kapacity C válcových elektrod:
\[Q\,=\,CU.\]
Kapacita C válcového kondenzátoru je dána vztahem:
\[ C\,=\,\frac{2\pi \epsilon}{\ln{\frac{b}{a}}}L\,, \]
kde ε je permitivita prostředí, L je délka válcového kondenzátoru a a, b jsou poloměry válců, které tvoří kondenzátor (a < b).
Nápověda 4
Uvědomte si nebo vyhledejte, jak vypadá Ohmův zákon v diferenciálním tvaru.
Řešení nápovědy 4
Ohmův zákon pro homogenní vodiče v diferenciálním tvaru je dán vztahem:
\[ \vec{j}\,=\,\sigma \vec{E}, \]
kde \(\vec{j}\) je hustota elektrického proudu, σ měrná elektrická vodivost a \(\vec{E}\) značí intenzitu elektrického pole.

Pomocí takto zapsaného Ohmova zákona vyjádříme intenzitu el. pole do Gaussovy věty elektrostatiky.
III. Rozbor
Odpor mezi elektrodami vypočítáme pomocí formální analogie s elektrostatickým polem.

Uvažujme, že elektrody jsou vnořeny do dielektrika o určité permitivitě a jsou na ně přivedeny náboje stejné velikosti, ale opačného znamení tak, že udržují původní hodnoty potenciálů. V takovém případě bude mezi elektrodami stejný průběh elektrické intenzity. Náboj vyjádříme z Gaussovy věty elektrostatiky v integrálním tvaru. Vztah mezi velikostí náboje a rozdílem potenciálů vyjádříme pomocí kapacity válcových elektrod.

Proud procházející mezi elektrodami vyjádříme pomocí proudové hustoty a Ohmova zákona v diferenciálním tvaru, tj. pomocí intenzity elektrického pole.

Takto získanou rovnici pro proud procházející mezi elektrodami spojíme s vyjádřením elektrického náboje. Pomocí Ohmova zákona vypočítáme odpor mezi válcovými elektrodami jako podíl napětí mezi elektrodami a celkového proudu, který mezi nimi prochází.
III. Řešení
Uvažujme, že mezi elektrodami je místo vodiče dielektrikum o permitivitě ε a jsou na ně přivedeny náboje stejné velikosti Q, ale opačného znamení tak, že udržují původní hodnoty potenciálů. V řešení využijeme toho, že průběh elektrické intenzity je jak v tomto statickém případě, tak ve stacionárním případě, kdy mezi elektrodami protéká ustálený proud, stejný.

Vztah mezi velikostí náboje Q a rozdílem potenciálů = napětím U vyjádříme pomocí kapacity C válcových elektrod:
\[Q\,=\,UC.\tag{*}\]
Gaussova věta elektrostatiky v integrálním tvaru říká:
\[ \oint \vec{E}\cdot\mathrm{d}\vec{S}\,=\,\frac{Q}{\epsilon}\,. \]
Značka \(\normalsize{\oint}\) vyjadřuje, že plošný integrál je brán přes uzavřenou plochu, \(\vec{E}\) je intenzita elektrického pole, Q náboj přivedený na válcové elektrody povrchu S a ε je permitivita dané látky.

Ohmův zákon pro homogenní vodiče v diferenciálním tvaru je dán vztahem:
\[\vec{j}\,=\,\sigma \vec{E},\]
kde \(\vec{j}\) je hustota elektrického proudu, σ měrná elektrická vodivost a \(\vec{E}\) značí intenzitu elektrického pole.

Proud I procházející mezi elektrodami si vyjádříme pomocí hustoty proudu \(\vec{j\,}\):
\[ I\,=\,\oint \vec{j\,}\cdot\mathrm{d}\vec{S}. \]
Hustotu proudu určíme z Ohmova zákona a Gaussovy věty:
\[ I\,=\,\oint \sigma \vec{E}\cdot\mathrm{d}\vec{S}\,=\,\sigma\oint\vec{E}\cdot\mathrm{d}\vec{S}\,=\,\sigma\frac{Q}{\epsilon}\,. \]
Za náboj Q do této rovnice dosadíme vztah (*):
\[ I\,=\,\sigma\frac{CU}{\epsilon}\,. \]
Kapacita válcového kondenzátoru je dána vztahem:
\[ C\,=\,\frac{2\pi\epsilon}{\ln{\frac{b}{a}}}L\,, \]
kde ε je permitivita prostředí, L je výška válcového kondenzátoru a a, b jsou poloměry válců, které tvoří kondenzátor – poloměry válcových elektrod, přičemž a < b.

Dosazením kapacity získáme rovnici pro výpočet proudu procházejícího mezi válcovými elektrodami:
\[ I\,=\,\sigma\frac{\frac{2\pi\epsilon}{\ln{\frac{b}{a}}}L\,U}{\epsilon}\,=\,\frac{2\pi\sigma L}{\ln{\frac{b}{a}}}\,U. \]
Odpor mezi válcovými elektrodami vypočítáme jako podíl napětí U mezi elektrodami a proudu I, který mezi elektrodami prochází:
\[ R\,=\,\frac{U}{I}\,=\, \frac{U}{\frac{2\pi\sigma L}{\ln{\frac{b}{a}}}\,U}\,=\,\frac{\ln{\frac{b}{a}}}{2\pi\sigma L}\,. \]
Odpověď
Celkový elektrický odpor mezi válcovými elektrodami o poloměrech a a b vypočítáme ze vztahu:
\[ R\,=\,\frac{\ln{\frac{b}{a}}}{2\pi\sigma L}\,\mathrm{,} \]
pro proud procházející mezi těmito elektrodami o poloměrech a a b platí:
\[ I\,=\,\frac{2\pi\sigma L}{\ln{\left(\frac{b}{a}\right)}}\,U\mathrm{,} \]
kde σ je vodivost materiálu mezi elektrodami, L je délka elektrod a U značí napětí mezi elektrodami.

Poznámka: Všemi třemi způsoby řešení jsme získali stejný výsledek.
Odkaz na podobnou úlohu
Podobnou těžší úlohou je úloha Nehomogenní prostředí mezi válcovými elektrodami.